The SIMLIN Procedure
In this example, the SIMLIN procedure simulates a model of the U.S. economy called Klein’s Model I. The SAS data set KLEIN is used as input to the SYSLIN and SIMLIN procedures.
data klein;
input year c p w i x wp g t k wsum;
date=mdy(1,1,year);
format date year.;
y = c + i + g - t;
yr = year - 1931;
klag = lag( k );
plag = lag( p );
xlag = lag( x );
if year >= 1921;
label c ='consumption'
p ='profits'
w ='private wage bill'
i ='investment'
k ='capital stock'
y ='national income'
x ='private production'
wsum='total wage bill'
wp ='govt wage bill'
g ='govt demand'
t ='taxes'
klag='capital stock lagged'
plag='profits lagged'
xlag='private product lagged'
yr ='year-1931';
datalines;
1920 . 12.7 . . 44.9 . . . 182.8 .
1921 41.9 12.4 25.5 -0.2 45.6 2.7 3.9 7.7 182.6 28.2
... more lines ...
First, the model is specified and estimated using the SYSLIN procedure, and the parameter estimates are written to an OUTEST= data set. The printed output produced by the SYSLIN procedure is not shown here; see Example 29.1 in Chapter 29 for the printed output of the PROC SYSLIN step.
title1 'Simulation of Klein''s Model I using SIMLIN'; proc syslin 3sls data=klein outest=a; instruments klag plag xlag wp g t yr; endogenous c p w i x wsum k y; consume: model c = p plag wsum; invest: model i = p plag klag; labor: model w = x xlag yr; product: identity x = c + i + g; income: identity y = c + i + g - t; profit: identity p = x - w - t; stock: identity k = klag + i; wage: identity wsum = w + wp; run;
The OUTEST= data set A created by the SYSLIN procedure contains parameter estimates to be used by the SIMLIN procedure. The OUTEST= data set is shown in Output 25.1.1.
Output 25.1.1: The OUTEST= Data Set Created by PROC SYSLIN
| Simulation of Klein's Model I using SIMLIN |
| Obs | _TYPE_ | _STATUS_ | _MODEL_ | _DEPVAR_ | _SIGMA_ | Intercept | klag | plag | xlag | wp | g | t | yr | c | p | w | i | x | wsum | k | y |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | INST | 0 Converged | FIRST | c | 2.11403 | 58.3018 | -0.14654 | 0.74803 | 0.23007 | 0.19327 | 0.20501 | -0.36573 | 0.70109 | -1 | . | . | . | . | . | . | . |
| 2 | INST | 0 Converged | FIRST | p | 2.18298 | 50.3844 | -0.21610 | 0.80250 | 0.02200 | -0.07961 | 0.43902 | -0.92310 | 0.31941 | . | -1.00000 | . | . | . | . | . | . |
| 3 | INST | 0 Converged | FIRST | w | 1.75427 | 43.4356 | -0.12295 | 0.87192 | 0.09533 | -0.44373 | 0.86622 | -0.60415 | 0.71358 | . | . | -1 | . | . | . | . | . |
| 4 | INST | 0 Converged | FIRST | i | 1.72376 | 35.5182 | -0.19251 | 0.92639 | -0.11274 | -0.71661 | 0.10023 | -0.16152 | 0.33190 | . | . | . | -1 | . | . | . | . |
| 5 | INST | 0 Converged | FIRST | x | 3.77347 | 93.8200 | -0.33906 | 1.67442 | 0.11733 | -0.52334 | 1.30524 | -0.52725 | 1.03299 | . | . | . | . | -1.00000 | . | . | . |
| 6 | INST | 0 Converged | FIRST | wsum | 1.75427 | 43.4356 | -0.12295 | 0.87192 | 0.09533 | 0.55627 | 0.86622 | -0.60415 | 0.71358 | . | . | . | . | . | -1.00000 | . | . |
| 7 | INST | 0 Converged | FIRST | k | 1.72376 | 35.5182 | 0.80749 | 0.92639 | -0.11274 | -0.71661 | 0.10023 | -0.16152 | 0.33190 | . | . | . | . | . | . | -1 | . |
| 8 | INST | 0 Converged | FIRST | y | 3.77347 | 93.8200 | -0.33906 | 1.67442 | 0.11733 | -0.52334 | 1.30524 | -1.52725 | 1.03299 | . | . | . | . | . | . | . | -1 |
| 9 | 3SLS | 0 Converged | CONSUME | c | 1.04956 | 16.4408 | . | 0.16314 | . | . | . | . | . | -1 | 0.12489 | . | . | . | 0.79008 | . | . |
| 10 | 3SLS | 0 Converged | INVEST | i | 1.60796 | 28.1778 | -0.19485 | 0.75572 | . | . | . | . | . | . | -0.01308 | . | -1 | . | . | . | . |
| 11 | 3SLS | 0 Converged | LABOR | w | 0.80149 | 1.7972 | . | . | 0.18129 | . | . | . | 0.14967 | . | . | -1 | . | 0.40049 | . | . | . |
| 12 | IDENTITY | 0 Converged | PRODUCT | x | . | 0.0000 | . | . | . | . | 1.00000 | . | . | 1 | . | . | 1 | -1.00000 | . | . | . |
| 13 | IDENTITY | 0 Converged | INCOME | y | . | 0.0000 | . | . | . | . | 1.00000 | -1.00000 | . | 1 | . | . | 1 | . | . | . | -1 |
| 14 | IDENTITY | 0 Converged | PROFIT | p | . | 0.0000 | . | . | . | . | . | -1.00000 | . | . | -1.00000 | -1 | . | 1.00000 | . | . | . |
| 15 | IDENTITY | 0 Converged | STOCK | k | . | 0.0000 | 1.00000 | . | . | . | . | . | . | . | . | . | 1 | . | . | -1 | . |
| 16 | IDENTITY | 0 Converged | WAGE | wsum | . | 0.0000 | . | . | . | 1.00000 | . | . | . | . | . | 1 | . | . | -1.00000 | . | . |
Using the OUTEST= data set A produced by the SYSLIN procedure, the SIMLIN procedure can now compute the reduced form and simulate the model. The following statements perform the simulation.
title1 'Simulation of Klein''s Model I using SIMLIN';
proc simlin data=klein
est=a type=3sls
estprint
total interim=2
outest=b;
endogenous c p w i x wsum k y;
exogenous wp g t yr;
lagged klag k 1 plag p 1 xlag x 1;
id year;
output out=c p=chat phat what ihat xhat wsumhat khat yhat
r=cres pres wres ires xres wsumres kres yres;
run;
The reduced form coefficients and multipliers are added to the information read from EST= data set A and written to the OUTEST= data set B. The predicted and residual values from the simulation are written to the OUT= data set C specified in the OUTPUT statement.
The SIMLIN procedure first prints the structural coefficient matrices read from the EST= data set, as shown in Output 25.1.2 through Output 25.1.4.
Output 25.1.2: SIMLIN Procedure Output – Endogenous Structural Coefficients
| Simulation of Klein's Model I using SIMLIN |
| Structural Coefficients for Endogenous Variables | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variable | c | p | w | i | x | wsum | k | y |
| c | 1.0000 | -0.1249 | . | . | . | -0.7901 | . | . |
| i | . | 0.0131 | . | 1.0000 | . | . | . | . |
| w | . | . | 1.0000 | . | -0.4005 | . | . | . |
| x | -1.0000 | . | . | -1.0000 | 1.0000 | . | . | . |
| y | -1.0000 | . | . | -1.0000 | . | . | . | 1.0000 |
| p | . | 1.0000 | 1.0000 | . | -1.0000 | . | . | . |
| k | . | . | . | -1.0000 | . | . | 1.0000 | . |
| wsum | . | . | -1.0000 | . | . | 1.0000 | . | . |
Output 25.1.3: SIMLIN Procedure Output – Lagged Endogenous Structural Coefficients
| Structural Coefficients for Lagged Endogenous Variables |
|||
|---|---|---|---|
| Variable | klag | plag | xlag |
| c | . | 0.1631 | . |
| i | -0.1948 | 0.7557 | . |
| w | . | . | 0.1813 |
| x | . | . | . |
| y | . | . | . |
| p | . | . | . |
| k | 1.0000 | . | . |
| wsum | . | . | . |
Output 25.1.4: SIMLIN Procedure Output – Exogenous Structural Coefficients
| Structural Coefficients for Exogenous Variables | |||||
|---|---|---|---|---|---|
| Variable | wp | g | t | yr | Intercept |
| c | . | . | . | . | 16.4408 |
| i | . | . | . | . | 28.1778 |
| w | . | . | . | 0.1497 | 1.7972 |
| x | . | 1.0000 | . | . | 0 |
| y | . | 1.0000 | -1.0000 | . | 0 |
| p | . | . | -1.0000 | . | 0 |
| k | . | . | . | . | 0 |
| wsum | 1.0000 | . | . | . | 0 |
The SIMLIN procedure then prints the inverse of the endogenous variables coefficient matrix, as shown in Output 25.1.5.
Output 25.1.5: SIMLIN Procedure Output – Inverse Coefficient Matrix
| Inverse Coefficient Matrix for Endogenous Variables | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variable | c | i | w | x | y | p | k | wsum |
| c | 1.6347 | 0.6347 | 1.0957 | 0.6347 | 0 | 0.1959 | 0 | 1.2915 |
| p | 0.9724 | 0.9724 | -0.3405 | 0.9724 | 0 | 1.1087 | 0 | 0.7682 |
| w | 0.6496 | 0.6496 | 1.4406 | 0.6496 | 0 | 0.0726 | 0 | 0.5132 |
| i | -0.0127 | 0.9873 | 0.004453 | -0.0127 | 0 | -0.0145 | 0 | -0.0100 |
| x | 1.6219 | 1.6219 | 1.1001 | 1.6219 | 0 | 0.1814 | 0 | 1.2815 |
| wsum | 0.6496 | 0.6496 | 1.4406 | 0.6496 | 0 | 0.0726 | 0 | 1.5132 |
| k | -0.0127 | 0.9873 | 0.004453 | -0.0127 | 0 | -0.0145 | 1.0000 | -0.0100 |
| y | 1.6219 | 1.6219 | 1.1001 | 0.6219 | 1.0000 | 0.1814 | 0 | 1.2815 |
The SIMLIN procedure next prints the reduced form coefficient matrices, as shown in Output 25.1.6.
Output 25.1.6: SIMLIN Procedure Output – Reduced Form Coefficients
| Reduced Form for Lagged Endogenous Variables | |||
|---|---|---|---|
| Variable | klag | plag | xlag |
| c | -0.1237 | 0.7463 | 0.1986 |
| p | -0.1895 | 0.8935 | -0.0617 |
| w | -0.1266 | 0.5969 | 0.2612 |
| i | -0.1924 | 0.7440 | 0.000807 |
| x | -0.3160 | 1.4903 | 0.1994 |
| wsum | -0.1266 | 0.5969 | 0.2612 |
| k | 0.8076 | 0.7440 | 0.000807 |
| y | -0.3160 | 1.4903 | 0.1994 |
| Reduced Form for Exogenous Variables | |||||
|---|---|---|---|---|---|
| Variable | wp | g | t | yr | Intercept |
| c | 1.2915 | 0.6347 | -0.1959 | 0.1640 | 46.7273 |
| p | 0.7682 | 0.9724 | -1.1087 | -0.0510 | 42.7736 |
| w | 0.5132 | 0.6496 | -0.0726 | 0.2156 | 31.5721 |
| i | -0.0100 | -0.0127 | 0.0145 | 0.000667 | 27.6184 |
| x | 1.2815 | 1.6219 | -0.1814 | 0.1647 | 74.3457 |
| wsum | 1.5132 | 0.6496 | -0.0726 | 0.2156 | 31.5721 |
| k | -0.0100 | -0.0127 | 0.0145 | 0.000667 | 27.6184 |
| y | 1.2815 | 1.6219 | -1.1814 | 0.1647 | 74.3457 |
The multiplier matrices (requested by the INTERIM=2 and TOTAL options) are printed next, as shown in Output 25.1.7 and Output 25.1.8.
Output 25.1.7: SIMLIN Procedure Output – Interim Multipliers
| Interim Multipliers for Interim 1 | |||||
|---|---|---|---|---|---|
| Variable | wp | g | t | yr | Intercept |
| c | 0.829130 | 1.049424 | -0.865262 | -.0054080 | 43.27442 |
| p | 0.609213 | 0.771077 | -0.982167 | -.0558215 | 28.39545 |
| w | 0.794488 | 1.005578 | -0.710961 | 0.0125018 | 41.45124 |
| i | 0.574572 | 0.727231 | -0.827867 | -.0379117 | 26.57227 |
| x | 1.403702 | 1.776655 | -1.693129 | -.0433197 | 69.84670 |
| wsum | 0.794488 | 1.005578 | -0.710961 | 0.0125018 | 41.45124 |
| k | 0.564524 | 0.714514 | -0.813366 | -.0372452 | 54.19068 |
| y | 1.403702 | 1.776655 | -1.693129 | -.0433197 | 69.84670 |
| Interim Multipliers for Interim 2 | |||||
|---|---|---|---|---|---|
| Variable | wp | g | t | yr | Intercept |
| c | 0.663671 | 0.840004 | -0.968727 | -.0456589 | 28.36428 |
| p | 0.350716 | 0.443899 | -0.618929 | -.0401446 | 10.79216 |
| w | 0.658769 | 0.833799 | -0.925467 | -.0399178 | 28.33114 |
| i | 0.345813 | 0.437694 | -0.575669 | -.0344035 | 10.75901 |
| x | 1.009485 | 1.277698 | -1.544396 | -.0800624 | 39.12330 |
| wsum | 0.658769 | 0.833799 | -0.925467 | -.0399178 | 28.33114 |
| k | 0.910337 | 1.152208 | -1.389035 | -.0716486 | 64.94969 |
| y | 1.009485 | 1.277698 | -1.544396 | -.0800624 | 39.12330 |
Output 25.1.8: SIMLIN Procedure Output – Total Multipliers
| Total Multipliers | |||||
|---|---|---|---|---|---|
| Variable | wp | g | t | yr | Intercept |
| c | 1.881667 | 1.381613 | -0.685987 | 0.1789624 | 41.3045 |
| p | 0.786945 | 0.996031 | -1.286891 | -.0748290 | 15.4770 |
| w | 1.094722 | 1.385582 | -0.399095 | 0.2537914 | 25.8275 |
| i | 0.000000 | 0.000000 | -0.000000 | 0.0000000 | 0.0000 |
| x | 1.881667 | 2.381613 | -0.685987 | 0.1789624 | 41.3045 |
| wsum | 2.094722 | 1.385582 | -0.399095 | 0.2537914 | 25.8275 |
| k | 2.999365 | 3.796275 | -4.904859 | -.2852032 | 203.6035 |
| y | 1.881667 | 2.381613 | -1.685987 | 0.1789624 | 41.3045 |
The last part of the SIMLIN procedure output is a table of statistics of fit for the simulation, as shown in Output 25.1.9.
Output 25.1.9: SIMLIN Procedure Output – Simulation Statistics
| Fit Statistics | ||||||||
|---|---|---|---|---|---|---|---|---|
| Variable | N | Mean Error | Mean Pct Error |
Mean Abs Error | Mean Abs Pct Error |
RMS Error |
RMS Pct Error |
Label |
| c | 21 | 0.1367 | -0.3827 | 3.5011 | 6.69769 | 4.3155 | 8.1701 | consumption |
| p | 21 | 0.1422 | -4.0671 | 2.9355 | 19.61400 | 3.4257 | 26.0265 | profits |
| w | 21 | 0.1282 | -0.8939 | 3.1247 | 8.92110 | 4.0930 | 11.4709 | private wage bill |
| i | 21 | 0.1337 | 105.8529 | 2.4983 | 127.13736 | 2.9980 | 252.3497 | investment |
| x | 21 | 0.2704 | -0.9553 | 5.9622 | 10.40057 | 7.1881 | 12.5653 | private production |
| wsum | 21 | 0.1282 | -0.6669 | 3.1247 | 7.88988 | 4.0930 | 10.1724 | total wage bill |
| k | 21 | -0.1424 | -0.1506 | 3.8879 | 1.90614 | 5.0036 | 2.4209 | capital stock |
| y | 21 | 0.2704 | -1.3476 | 5.9622 | 11.74177 | 7.1881 | 14.2214 | national income |
The OUTEST= output data set contains all the observations read from the EST= data set, and in addition contains observations for the reduced form and multiplier matrices. The following statements produce a partial listing of the OUTEST= data set, as shown in Output 25.1.10.
proc print data=b; where _type_ = 'REDUCED' | _type_ = 'IMULT1'; run;
Output 25.1.10: Partial Listing of OUTEST= Data Set
| Simulation of Klein's Model I using SIMLIN |
| Obs | _TYPE_ | _DEPVAR_ | _MODEL_ | _SIGMA_ | c | p | w | i | x | wsum | k | y | klag | plag | xlag | wp | g | t | yr | Intercept |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | REDUCED | c | . | 1.63465 | 0.63465 | 1.09566 | 0.63465 | 0 | 0.19585 | 0 | 1.29151 | -0.12366 | 0.74631 | 0.19863 | 1.29151 | 0.63465 | -0.19585 | 0.16399 | 46.7273 | |
| 10 | REDUCED | p | . | 0.97236 | 0.97236 | -0.34048 | 0.97236 | 0 | 1.10872 | 0 | 0.76825 | -0.18946 | 0.89347 | -0.06173 | 0.76825 | 0.97236 | -1.10872 | -0.05096 | 42.7736 | |
| 11 | REDUCED | w | . | 0.64957 | 0.64957 | 1.44059 | 0.64957 | 0 | 0.07263 | 0 | 0.51321 | -0.12657 | 0.59687 | 0.26117 | 0.51321 | 0.64957 | -0.07263 | 0.21562 | 31.5721 | |
| 12 | REDUCED | i | . | -0.01272 | 0.98728 | 0.00445 | -0.01272 | 0 | -0.01450 | 0 | -0.01005 | -0.19237 | 0.74404 | 0.00081 | -0.01005 | -0.01272 | 0.01450 | 0.00067 | 27.6184 | |
| 13 | REDUCED | x | . | 1.62194 | 1.62194 | 1.10011 | 1.62194 | 0 | 0.18135 | 0 | 1.28146 | -0.31603 | 1.49034 | 0.19944 | 1.28146 | 1.62194 | -0.18135 | 0.16466 | 74.3457 | |
| 14 | REDUCED | wsum | . | 0.64957 | 0.64957 | 1.44059 | 0.64957 | 0 | 0.07263 | 0 | 1.51321 | -0.12657 | 0.59687 | 0.26117 | 1.51321 | 0.64957 | -0.07263 | 0.21562 | 31.5721 | |
| 15 | REDUCED | k | . | -0.01272 | 0.98728 | 0.00445 | -0.01272 | 0 | -0.01450 | 1 | -0.01005 | 0.80763 | 0.74404 | 0.00081 | -0.01005 | -0.01272 | 0.01450 | 0.00067 | 27.6184 | |
| 16 | REDUCED | y | . | 1.62194 | 1.62194 | 1.10011 | 0.62194 | 1 | 0.18135 | 0 | 1.28146 | -0.31603 | 1.49034 | 0.19944 | 1.28146 | 1.62194 | -1.18135 | 0.16466 | 74.3457 | |
| 17 | IMULT1 | c | . | . | . | . | . | . | . | . | . | . | . | . | 0.82913 | 1.04942 | -0.86526 | -0.00541 | 43.2744 | |
| 18 | IMULT1 | p | . | . | . | . | . | . | . | . | . | . | . | . | 0.60921 | 0.77108 | -0.98217 | -0.05582 | 28.3955 | |
| 19 | IMULT1 | w | . | . | . | . | . | . | . | . | . | . | . | . | 0.79449 | 1.00558 | -0.71096 | 0.01250 | 41.4512 | |
| 20 | IMULT1 | i | . | . | . | . | . | . | . | . | . | . | . | . | 0.57457 | 0.72723 | -0.82787 | -0.03791 | 26.5723 | |
| 21 | IMULT1 | x | . | . | . | . | . | . | . | . | . | . | . | . | 1.40370 | 1.77666 | -1.69313 | -0.04332 | 69.8467 | |
| 22 | IMULT1 | wsum | . | . | . | . | . | . | . | . | . | . | . | . | 0.79449 | 1.00558 | -0.71096 | 0.01250 | 41.4512 | |
| 23 | IMULT1 | k | . | . | . | . | . | . | . | . | . | . | . | . | 0.56452 | 0.71451 | -0.81337 | -0.03725 | 54.1907 | |
| 24 | IMULT1 | y | . | . | . | . | . | . | . | . | . | . | . | . | 1.40370 | 1.77666 | -1.69313 | -0.04332 | 69.8467 |
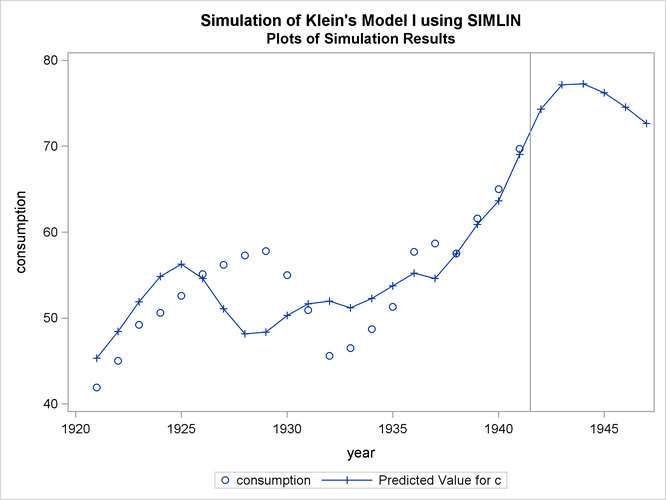
The actual and predicted values for the variable C are plotted in Output 25.1.11.
title2 'Plots of Simulation Results'; proc sgplot data=c; scatter x=year y=c; series x=year y=chat / markers markerattrs=(symbol=plus); refline 1941.5 / axis=x; run;