The MODEL Procedure

Example 19.16 Simulated Method of Moments—AR(1) Process

This example illustrates how to use SMM to estimate an AR(1) regression model for the following process:

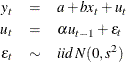
\begin{eqnarray*} y_ t & =& a + b x_ t + u_ t \\ u_ t & =& \alpha u_{t-1} + \epsilon _ t \\ \epsilon _ t & \sim & iid \, N(0, s^2) \nonumber \end{eqnarray*}

In the following SAS statements, $\mathit{ysim}$ is simulated by using this model, and the endogenous variable y is set to be equal to $\mathit{ysim}$. The MOMENT statement creates two more moments for the estimation. One is the second moment, and the other is the first-order autocovariance. The NPREOBS=10 option instructs PROC MODEL to run the simulation 10 times before $\mathit{ysim}$ is compared to the first observation of y. Because the initial $\mbox{zlag}(u)$ is zero, the first $\mathit{ysim}$ is $a + b * x + s * \mbox{rannor}(8003)$. Without the NPREOBS option, this $\mathit{ysim}$ is matched with the first observation of y. With NPREOBS, this $\mathit{ysim}$ and the next nine $\mathit{ysim}$ are thrown away, and the moment match starts with the eleventh $\mathit{ysim}$ with the first observation of y. This way, the initial values do not exert a large influence on the simulated endogenous variables. 

%let nobs=500;
data ardata;
   lu =0;
   do i=-10 to &nobs;
      x = rannor( 1011 );
      e = rannor( 1011 );
      u = .6 * lu + 1.5 * e;
      Y = 2 + 1.5 * x + u;
      lu = u;
      if i > 0 then output;
   end;
run;

title1 'Simulated Method of Moments for AR(1) Process';

proc model data=ardata ;
   parms a b s 1 alpha .5;
   instrument x;

   u = alpha * zlag(u) + s * rannor( 8003 );
   ysim = a + b * x + u;
   y = ysim;
   moment y = (2) lag1(1);

   fit y / gmm npreobs=10 ndraw=10;
   bound s > 0, 1 > alpha > 0;
run;

The output of the MODEL procedure is shown in Output 19.16.1:

Output 19.16.1: PROC MODEL Output

Simulated Method of Moments for AR(1) Process

The MODEL Procedure

Model Summary
Model Variables 1
Parameters 4
Equations 3
Number of Statements 8
Program Lag Length 1

Model Variables Y
Parameters(Value) a b s(1) alpha(0.5)
Equations _moment_2 _moment_1 Y

The 3 Equations to Estimate
_moment_2 = F(a, b, s, alpha)
_moment_1 = F(a, b, s, alpha)
Y = F(a(1), b(x), s, alpha)
Instruments 1 x

Nonlinear GMM Parameter Estimates
Parameter Estimate Approx Std Err t Value Approx
Pr > |t|
a 1.632798 0.1038 15.73 <.0001
b 1.513197 0.0698 21.67 <.0001
s 1.427888 0.0984 14.52 <.0001
alpha 0.543985 0.0809 6.72 <.0001