The PANEL Procedure

MODEL Statement

  • MODEL response = regressors </ options>;

The MODEL statement specifies the regression model and the error structure assumed for the regression residuals. The response variable on the left side of the equal sign is regressed on the independent variables listed after the equal sign. Any number of MODEL statements can be used. For each model statement, only one response variable can be specified on the left side of the equal sign.

The error structure is specified by the PARKS, DASILVA, FIXONE, FIXONETIME, FIXTWO, FDONE, FDONETIME, FDTWO, RANONE, RANTWO, GMM1, GMM2, and ITGMM options. More than one of these options can be used, in which case the analysis is repeated for each error structure model specified.

Models can be given labels. Model labels are used in the printed output to identify the results for different models. If no label is specified, the response variable name is used as the label for the model. The model label is specified as follows:

label : MODEL …;

The following options can be specified in the MODEL statement after a slash (/).

ARTEST=integer

specifies the maximum order of the test for the presence of AR effects in the residual in the dynamic panel model. The acceptable range of values for this option is 1 to $t-3$.

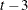ATOL=number

specifies the convergence criterion for iterated GMM when convergence of the method is determined by convergence in the weighting matrix. The convergence criterion must be positive. The default option is the BTOL= option unless the ATOL= option is specified. See the section Dynamic Panel Estimator for details.

BANDOPT=TRAILING | CENTERED | LEADING

specifies which observations are included in the instrument list when the MAXBAND= option is specified. This option should be used only for exogenous instruments. BANDOPT=TRAILING is the default. See the section Dynamic Panel Estimator for details.

BFN

requests the R$_{\rho }$ statistic for serial correlation under cross-sectional fixed effects.

BIASCORRECTED

requests that the bias-corrected covariance matrix of the two-step dynamic panel estimator be computed. When you specify this option, the ROBUST option is disabled for the two-step GMM estimator. For more information, see the section Dynamic Panel Estimator.

BL91

requests the Baltagi and Li (1991) joint LM test for serial correlation and random cross-sectional effects.

BL95

requests the Baltagi and Li (1995) LM test for first-order correlation under fixed effects.

BP

requests the Breusch-Pagan one-way test for random effects.

BP2

requests the Breusch-Pagan two-way test for random effects.

BSY

requests the Bera, Sosa Escudero, and Yoon modified Rao’s score test for random cross-sectional effects or serial correlation or both.

BTOL=number

specifies the convergence criterion for iterated GMM when convergence of the method is determined by convergence in the parameter matrix. The convergence criterion must be positive. The default is BTOL=1E–8. See the section Dynamic Panel Estimator for details.

BTWNG

specifies that a between-groups model be estimated.

BTWNT

specifies that a between-time-periods model be estimated.

BW

requests the Berenblut-Webb statistic for serial correlation under cross-sectional fixed effects.

CDTEST <(P=value) >

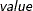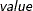requests cross-sectional dependence tests. These include the Breusch and Pagan (1980) LM test, the scaled version of the Breusch and Pagan (1980) test, and the Pesaran (2004) CD test. When you specify P=value, the CD test for local cross-sectional dependence is performed with the order $\Argument{value}$ where $\Argument{value}$ is an integer greater than zero.

CLUSTER

specifies the cluster correction for the covariance matrix. The cluster correction can be requested with HCCME=0, 1, 2 or 3.

CORRB
CORR

prints the matrix of estimated correlations between the parameter estimates.

COVB
VAR

prints the matrix of estimated covariances between the parameter estimates.

DASILVA

specifies that the model be estimated by using the Da Silva method, which assumes a mixed variance-component moving average model for the error structure. See the section Da Silva Method (Variance-Component Moving Average Model) for details.

DW

requests the Durbin-Watson statistic for serial correlation under cross-sectional fixed effects.

FDONE

requests that a one-way model be estimated by using first-differenced methods.

FDONETIME

requests that a one-way model that corresponds to time effects be estimated by using first-differenced methods.

FDTWO

requests that a two-way model be estimated by using first-differenced methods.

FIXONE

specifies that a one-way fixed-effects model be estimated with the one-way model corresponding to cross-sectional effects only.

FIXONETIME

specifies that a one-way fixed-effects model be estimated with the one-way model corresponding to time effects only.

FIXTWO

specifies that a two-way fixed-effects model be estimated.

GHM

requests the Gourieroux, Holly, and Monfort two-way test for random effects.

GINV= G2 | G4

specifies what type of generalized inverse to use. The default is a G2 inverse. The G4 inverse is generally more desirable except that it is a more numerically intensive methodology.

GMM1

requests that the model be estimated in a single step by using the dynamic panel estimator method, which allows for autoregressive processes. When you specify this option, you must specify one INSTRUMENT statement for each MODEL statement. For more information, see the section Dynamic Panel Estimator.

GMM2

requests that the model be estimated in two steps by using the dynamic panel estimator method. An initial first step is used to form an estimator for the weighting matrix that is used in the second step. For more information, see the section Dynamic Panel Estimator.

HAC <(hac-options) >

specifies the heteroscedasticity- and autocorrelation-consistent (HAC) covariance matrix estimator. This option is not available for between models and cannot be specified with the HCCME option. When you specify this option, you can also specify the following hac-options within parentheses:

KERNEL=value

specifies the type of kernel function. You can specify the following values:

BARTLETT

specifies the Bartlett kernel function.

PARZEN

specifies the Parzen kernel function.

QS

specifies the quadratic spectral kernel function.

TH

specifies the Turkey-Hanning kernel function.

TRUNCATED

specifies the truncated kernel function.

The default is KERNEL=TRUNCATED.

KERNELLB=number

specifies the lower bound of the kernel weight value. Any kernel weight less than this lower bound is regarded as 0, which accelerates the calculation for big samples, especially for the quadratic spectral kernel function. By default, KERNELLB=0.

BANDWIDTH=value

specifies the fixed bandwidth value or bandwidth selection method which is used in the kernel function. You can specify the following values:

ANDREWS91 | ANDREWS

specifies the Andrews (1991) bandwidth selection method.

NEWEYWEST94<(C=number)>
NW94 <(C=number)>

specifies the Newey and West (1994) bandwidth selection method. The C= option can be specified within parentheses for the calculation of lag selection parameter; the default is C=12.

SAMPLESIZE<(option-list)>
SS<(option-list)>

specifies that the bandwidth be calculated according to the following equation based on the sample size

\[ b=\gamma T^{r} + c \]

where b is the bandwidth parameter, T is the sample size, and 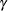$\gamma $, r and c are values specified by the following options within parentheses and separated by commas.

GAMMA=number

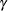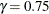specifies the coefficient $\gamma $ in the equation. The default is $\gamma =0.75$.

RATE=number

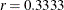specifies the growth rate r in the equation. The default is $r=0.3333$.

CONSTANT=number

specifies the constant c in the equation. The default is $c=0.5$.

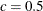INT

specifies that the bandwidth parameter must be integer; that is, 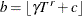$b=\left\lfloor {\gamma T^{r} + c}\right\rfloor $, where 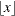$\left\lfloor {x}\right\rfloor $ denotes the largest integer less than or equal to x.

number

specifies the fixed value of the bandwidth parameter.

The default is BANDWIDTH=ANDREWS91.

PREWHITENING

specifies that prewhitening is required in the covariance calculation.

ADJUSTDF

specifies that the adjustment of degrees of freedom is required in the covariance calculation.
See the section Heteroscedasticity- and Autocorrelation-Consistent Covariance Matrices for details.

HCCME= NO | number

specifies the type of HCCME covariance matrix requested. If you specify HCCME=NO, the covariance matrix is not corrected. The value number can be any integer from 0 to 4, inclusive. See the section Heteroscedasticity-Corrected Covariance Matrices for details. By default, HCCME=NO.

HONDA

requests the Honda one-way test for random effects.

HONDA2

requests the Honda two-way test for random effects.

ITGMM

specifies that the model be estimated by using the dynamic panel estimator method, but that PROC PANEL keep updating the weighting matrix until either the parameter vector converges or the weighting matrix converges. See the section Dynamic Panel Estimator for details.

ITPRINT

prints out the iteration history of the parameter and transformed sum of error squared.

KW

requests the King and Wu two-way test for random effects.

M=number

specifies the order of the moving-average process in the Da Silva method. The value of the M=option must be less than 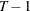${\mi{T}-1}$. The default is M=1.

MAXBAND=integer

specifies the maximum number of time periods (per instrumental variable) that are allowed into the moment condition. The acceptable range of values for this option is 1 to 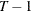$T-1$. If BANDOPT=LEADING or CENTERED, then the default value of MAXBAND is 2. If BANDOPT=TRAILING, then the default value of MAXBAND is 1. If no BANDOPT option is specified such as when no exogenous instruments are used, then the default value of MAXBAND is 1. See the section Dynamic Panel Estimator for details.

MAXITER=integer

specifies the maximum number of iterations allowed for the iterated GMM option. The default value is MAXITER=200. See the section Dynamic Panel Estimator for details.

NEWEYWEST=<(option-list)>

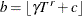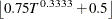specifies the well-known Newey-West estimator, a special HAC estimator with (1) the Bartlett kernel, (2) the bandwidth parameter determined by the equation based on the sample size, $b=\left\lfloor {\gamma T^{r} + c}\right\rfloor $, and (3) no adjustment for degrees of freedom and no prewhitening. By default the bandwidth parameter for Newey-West estimator is $\left\lfloor {0.75T^{0.3333}+0.5}\right\rfloor $, as shown in the equation (15.17) in Stock and Watson (2002). When you specify COVEST=NEWEYWEST, you can specify the following options in parentheses and separate them with commas:

GAMMA= number

specifies the coefficient $\gamma $ in the equation. The default is $\gamma =0.75$.

RATE= number

specifies the growth rate r in the equation. The default is $r=0.3333$.

CONSTANT= number

specifies the constant c in the equation. The default is $c=0.5$.

NODIFFS

specifies that the dynamic panel model be estimated without moment conditions from the difference equations. See the section Dynamic Panel Estimator for details.

NOESTIM

limits the estimation of a FIXONE, FIXONETIME, RANONE model to the generation of the transformed series. This option is intended for use with an OUTTRANS= data set.

NOINT

suppresses the intercept parameter from the model.

NOLEVELS

specifies that the dynamic panel model be estimated without moment conditions from the level equations. See the section Dynamic Panel Estimator for details.

NOPRINT

suppresses the normal printed output.

PARKS

specifies that the model be estimated by using the Parks method, which assumes a first-order autoregressive model for the error structure. See the section Parks Method (Autoregressive Model) for details.

PHI

prints the 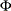${\Phi }$ matrix of estimated covariances of the observations for the Parks method. The PHI option is relevant only when the PARKS option is used. See the section Parks Method (Autoregressive Model) for details.

POOLED

specifies that a pooled (OLS) model be estimated.

POOLTEST

requests poolability tests for one-way fixed effects and pooled models.

PRINTFIXED

prints the fixed effects.

RANONE

specifies that a one-way random-effects model be estimated.

RANTWO

specifies that a two-way random-effects model be estimated.

RHO

prints the estimated autocorrelation coefficients for the Parks method.

ROBUST

specifies that the robust weighting matrix be used in the calculation of the covariance matrix of the single-step, two-step and iterated GMM dynamic panel estimator. See the section Dynamic Panel Estimator for details.

SINGULAR=number

specifies a singularity criterion for the inversion of the matrix. The default depends on the precision of the computer system.

TIME

specifies that the model be estimated by using the dynamic panel estimator method, but that PROC PANEL includes time dummy variables to model any time effects present in the data. See the section Dynamic Panel Estimator for details.

UROOTTEST(test1<(test-options), test2<(test-options)>…> < option1 < option2…> >)
STATIONARITY(test1<(test-options), test2<(test-options)>…> < option1 < option2…> >)

specifies tests of stationarity or unit root for panel data and the options for each test. The panel unit root test (or stationarity test ) will test the existence of unit root for the dependent variables only. Six tests are available. You can specify all or some of these tests, separated by commas. If you specify one or more test-options (separated by spaces) inside the parentheses after a particular test, they apply only to that test. If you specify one or more options separated by spaces after you specify the tests, they apply to all the tests. If you specify both test-options and options, the test-options override the options.

ALL

requests that all panel unit root and stationarity tests be performed.

BREITUNG<(test-options) >

requests Breitung’s unbiased test, t test and GLS t test that are robust to cross-sectional dependence. The tests are described in Breitung and Meyer (1994); Breitung (2000); Breitung and Das (2005). The following test-options are available for this test:

DETAIL

requests that intermediate results (lag order) be printed.

LAGS=type | value

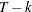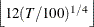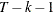specifies the method to choose the lag order for the augmented Dickey-Fuller (ADF) regressions. You can specify a value for the order of lags. If the specified lag order is too big to run linear regression (LAGS > $T-k$, where T is the number of observations and k is the number of parameters), then the lag order is set to $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $ or $T-k-1$, whichever is smaller. Alternatively, you can specify one of the following types:

GS

selects the order of lags by Hall’s (1994) sequential testing method: from the most general model (maximum lags) to lower order of lag terms.

SG

selects the order of lags by Hall’s (1994) sequential testing method: from no lag term to maximum allowed lags.

AIC

selects the order of lags by AIC.

SBC
SIC
SBIC

selects the order of lags by Bayesian information criterion (or Schwarz criterion).

HQIC

selects the order of lags by the Hannan-Quinn information criterion.

MAIC

selects the order of lags by the modified AIC that is proposed by Ng and Perron (2001).

The default is LAGS=MAIC.

MAXLAGS=value

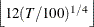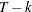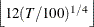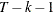specifies the maximum lag order that the model allows. The default value is $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $. If value is larger than 0 and larger than $T-k$, then the maximum lag order is set to be the default value of $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $ or $T-k-1$, whichever is smaller. This option is ignored if you specify LAGS=value.

COMBINATION < (test-options) >
FISHER < (test-options) >

specifies combination tests proposed by Choi (2001); Maddala and Wu (1999). Fisher’s test, as proposed by Maddala and Wu (1999), is a special case of combination tests. You can specify one or more of the following test-options:

TEST=ADF | PP

selects the time series unit root test for combination tests (Fisher’s test). ADF specifies the augmented Dickey-Fuller (ADF) test, and ignores the BANDWIDTH and KERNEL options for the combination tests. PP specifies the Phillips and Perron (1988) unit root test. When you specifies TEST = PP, the LAGS and MAXLAGS options are ignored for the combination tests.
The default is TEST=PP.

KERNEL=value

specifies the type of kernel function. You can specify the following values:

BARTLETT

specifies the Bartlett kernel function.

PARZEN

specifies the Parzen kernel function.

QS

specifies the quadratic spectral kernel function.

TH

specifies the Turkey-Hanning kernel function.

TRUNCATED

specifies the truncated kernel function.

The default is KERNEL=QS.

BANDWIDTH=ANDREWS | number

specifies the bandwidth for the kernel. If you specify BANDWIDTH=ANDREWS, the bandwidth is selected by the Andrews method. If you specify a nonnegative number, the bandwidth is set to that value. The default is BANDWIDTH=ANDREWS.

DETAIL

requests that intermediate results (lag order and long-run variance for each cross section) be printed.

LAGS=type | value

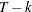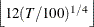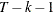specifies the method to choose the lag order for the augmented Dickey-Fuller (ADF) regressions. You can specify a value for the order of lags. If the specified lag order is too big to run linear regression (LAGS > $T-k$, where T is the number of observations and k is the number of parameters), then the lag order is set to $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $ or $T-k-1$, whichever is smaller. Alternatively, you can specify one of the following types:

GS

selects the order of lags by Hall’s (1994) sequential testing method: from the most general model (maximum lags) to lower order of lag terms.

SG

selects the order of lags by Hall’s (1994) sequential testing method: from no lag term to maximum allowed lags.

AIC

selects the order of lags by AIC.

SBC
SIC
SBIC

selects the order of lags by Bayesian information criterion (or Schwarz criterion).

HQIC

selects the order of lags by the Hannan-Quinn information criterion.

MAIC

selects the order of lags by the modified AIC that is proposed by Ng and Perron (2001).

The default is LAGS=MAIC.

MAXLAGS=value

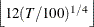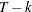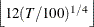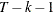specifies the maximum lag order that the model allows. The default value is $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $. If value is larger than 0 and larger than $T-k$, then the maximum lag order is set to be the default value of $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $ or $T-k-1$, whichever is smaller. This option is ignored if you specify LAGS=value.

HADRI < (test-options) >

specifies Hadri’s (2000) panel stationarity test. You can specify the following test-options:

DETAIL

requests that intermediate results (lag order and long-run variance for each cross section) be printed.

KERNEL=value

specifies the type of kernel function. You can specify the following values:

BARTLETT

specifies the Bartlett kernel function.

PARZEN

specifies the Parzen kernel function.

QS

specifies the quadratic spectral kernel function.

TH

specifies the Turkey-Hanning kernel function.

TRUNCATED

specifies the truncated kernel function.

The default is KERNEL=QS.

BANDWIDTH=ANDREWS | number

specifies the bandwidth for the kernel. If you specify BANDWIDTH=ANDREWS, the bandwidth is selected with the Andrews method. If you specify a nonnegative number, the bandwidth is set to that value. The default is BANDWIDTH=ANDREWS.

HT

specifies Harris and Tzavalis (1999) panel unit root test. No options are available for this test.

IPS < (test-options) >

specifies the Im, Pesaran, and Shin (2003) panel unit root test. You can specify the following test-options:

DETAIL

requests that intermediate results (lag order) be printed.

LAGS=type | value

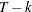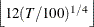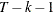specifies the method to choose the lag order for the augmented Dickey-Fuller (ADF) regressions. You can specify a value for the order of lags. If the specified lag order is too big to run linear regression (LAGS > $T-k$, where T is the number of observations and k is the number of parameters), then the lag order is set to $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $ or $T-k-1$, whichever is smaller. Alternatively, you can specify one of the following types:

GS

selects the order of lags by Hall’s (1994) sequential testing method: from the most general model (maximum lags) to lower order of lag terms.

SG

selects the order of lags by Hall’s (1994) sequential testing method: from no lag term to maximum allowed lags.

AIC

selects the order of lags by AIC.

SBC
SIC
SBIC

selects the order of lags by Bayesian information criterion (or Schwarz criterion).

HQIC

selects the order of lags by the Hannan-Quinn information criterion.

MAIC

selects the order of lags by the modified AIC that is proposed by Ng and Perron (2001).

The default is LAGS=MAIC.

MAXLAGS=value

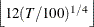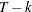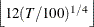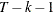specifies the maximum lag order that the model allows. The default value is $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $. If value is larger than 0 and larger than $T-k$, then the maximum lag order is set to be the default value of $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $ or $T-k-1$, whichever is smaller. This option is ignored if you specify LAGS=value.

LLC < (test-options) >

specifies the Levin, Lin, and Chu (2002) panel unit root test. You can specify the following test-options:

DETAIL

requests that intermediate results (lag order and long-run variance for each cross section) be printed.

KERNEL=value

specifies the type of kernel function. You can specify the following values:

BARTLETT

specifies the Bartlett kernel function.

PARZEN

specifies the Parzen kernel function.

QS

specifies the quadratic spectral kernel function.

TH

specifies the Turkey-Hanning kernel function.

TRUNCATED

specifies the truncated kernel function.

The default is KERNEL=QS.

BANDWIDTH=ANDREWS | number

specifies the bandwidth for the kernel. If you specify BANDWIDTH=ANDREWS, the bandwidth is selected with the Andrews method. If you specify a nonnegative number, the bandwidth is set to that value. The default is BANDWIDTH=LLCBAND, where the bandwidth is set to be 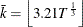$\bar{k}=\left\lfloor {3.21T^\frac {1}{3}}\right\rfloor $, according to Levin, Lin, and Chu (2002).

LAGS=type | value

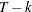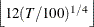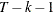specifies the method to choose the lag order for the augmented Dickey-Fuller (ADF) regressions. You can specify a value for the order of lags. If the specified lag order is too big to run linear regression (LAGS > $T-k$, where T is the number of observations and k is the number of parameters), then the lag order is set to $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $ or $T-k-1$, whichever is smaller. Alternatively, you can specify one of the following types:

GS

selects the order of lags by Hall’s (1994) sequential testing method: from the most general model (maximum lags) to lower order of lag terms.

SG

selects the order of lags by Hall’s (1994) sequential testing method: from no lag term to maximum allowed lags.

AIC

selects the order of lags by AIC.

SBC
SIC
SBIC

selects the order of lags by Bayesian information criterion (or Schwarz criterion).

HQIC

selects the order of lags by the Hannan-Quinn information criterion.

MAIC

selects the order of lags by the modified AIC that is proposed by Ng and Perron (2001).

The default is LAGS=MAIC.

MAXLAGS=value

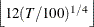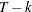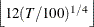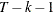specifies the maximum lag order that the model allows. The default value is $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $. If value is larger than 0 and larger than $T-k$, then the maximum lag order is set to be the default value of $\left\lfloor {12(T/100)^{1/4}}\right\rfloor $ or $T-k-1$, whichever is smaller. This option is ignored if you specify LAGS=value.

Two tests, LLC and BREITUNG’s, are specified in the following UROOTTEST option specification:

uroottest = (llc=(kernel=parzen lags=aic), breitung= (lags=gs ) maxlags=2 kernel=bartlett)

For the LLC test, the lag order is selected by AIC with maximum lag order 2, and the kernel is specified as Parzen (overriding Bartlett). For the BREITUNG’s test, the lag order is GS with a maximum lag order 2. The KERNEL option is ignored by BREITUNG’s test because it is not a valid option.

VCOMP=FB | NL | WH | WK

specifies the type of variance component estimate to use. The default is VCOMP=FB for balanced data and VCOMP=WK for unbalanced data. See the section One-Way Random-Effects Model and Two-Way Random-Effects Model for details.

WOOLDRIDGE02

requests the Wooldridge (2002) test for the presence of unobserved effects.