The PDLREG Procedure
This example estimates the demand for money by using the following dynamic specification:
where
-
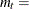 log of real money stock (M1)
log of real money stock (M1)
-
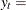 log of real GNP
log of real GNP
-
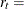 interest rate (commercial paper rate)
interest rate (commercial paper rate)
-
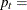 inflation rate
inflation rate
-
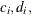 and
and 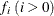 are coefficients for the lagged variables
are coefficients for the lagged variables
The following DATA step reads the data and transforms the real money and real GNP variables using the natural logarithm. Refer to Balke and Gordon (1986) for a description of the data.
data a;
input m1 gnp gdf r @@;
m = log( 100 * m1 / gdf );
lagm = lag( m );
y = log( gnp );
p = log( gdf / lag( gdf ) );
date = intnx( 'qtr', '1jan1968'd, _n_-1 );
format date yyqc6.;
label m = 'Real Money Stock (M1)'
lagm = 'Lagged Real Money Stock'
y = 'Real GNP'
r = 'Commercial Paper Rate'
p = 'Inflation Rate';
datalines;
187.15 1036.22 81.18 5.58
... more lines ...
Output 21.2.1 shows a partial list of the data set.
Output 21.2.1: Partial List of the Data Set A
| National Industrial Conference Board Data |
| Quarterly Series - 1952Q1 to 1967Q4 |
| Obs | date | m | lagm | y | r | p |
|---|---|---|---|---|---|---|
| 1 | 1968:1 | 5.44041 | . | 6.94333 | 5.58 | . |
| 2 | 1968:2 | 5.44732 | 5.44041 | 6.96226 | 6.08 | 0.011513 |
| 3 | 1968:3 | 5.45815 | 5.44732 | 6.97422 | 5.96 | 0.008246 |
| 4 | 1968:4 | 5.46492 | 5.45815 | 6.97661 | 5.96 | 0.014865 |
| 5 | 1969:1 | 5.46980 | 5.46492 | 6.98855 | 6.66 | 0.011005 |
The regression model is written for the PDLREG procedure with a MODEL statement. The LAGDEP= option is specified to test for the serial correlation in disturbances since regressors contain the lagged dependent variable LAGM.
title 'Money Demand Estimation using Distributed Lag Model'; title2 'Quarterly Data - 1968Q2 to 1983Q4'; proc pdlreg data=a; model m = lagm y(5,3) r(2, , ,first) p(3,2) / lagdep=lagm; run;
The estimated model is shown in Output 21.2.2 and Output 21.2.3.
Output 21.2.2: Parameter Estimates
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Variable | DF | Estimate | Standard Error |
t Value | Approx Pr > |t| |
| Intercept | 1 | -0.1407 | 0.2625 | -0.54 | 0.5943 |
| lagm | 1 | 0.9875 | 0.0425 | 23.21 | <.0001 |
| y**0 | 1 | 0.0132 | 0.004531 | 2.91 | 0.0055 |
| y**1 | 1 | -0.0704 | 0.0528 | -1.33 | 0.1891 |
| y**2 | 1 | 0.1261 | 0.0786 | 1.60 | 0.1154 |
| y**3 | 1 | -0.4089 | 0.1265 | -3.23 | 0.0022 |
| r**0 | 1 | -0.000186 | 0.000336 | -0.55 | 0.5816 |
| r**1 | 1 | 0.002200 | 0.000774 | 2.84 | 0.0065 |
| r**2 | 1 | 0.000788 | 0.000249 | 3.16 | 0.0027 |
| p**0 | 1 | -0.6602 | 0.1132 | -5.83 | <.0001 |
| p**1 | 1 | 0.4036 | 0.2321 | 1.74 | 0.0885 |
| p**2 | 1 | -1.0064 | 0.2288 | -4.40 | <.0001 |
Output 21.2.3: Estimates for Lagged Variables
| Estimate of Lag Distribution | |||||
|---|---|---|---|---|---|
| Variable | Estimate | Standard Error |
t Value | Approx Pr > |t| |
-0.196 0 0.2686 |
| y(0) | 0.268619 | 0.0910 | 2.95 | 0.0049 | | |************************| |
| y(1) | -0.196484 | 0.0612 | -3.21 | 0.0024 | |****************| | |
| y(2) | -0.163148 | 0.0537 | -3.04 | 0.0038 | | *************| | |
| y(3) | 0.063850 | 0.0451 | 1.42 | 0.1632 | | |****** | |
| y(4) | 0.179733 | 0.0588 | 3.06 | 0.0036 | | |**************** | |
| y(5) | -0.120276 | 0.0679 | -1.77 | 0.0827 | | *********| | |
| Estimate of Lag Distribution | |||||
|---|---|---|---|---|---|
| Variable | Estimate | Standard Error |
t Value | Approx Pr > |t| |
-1.104 0 0.2634 |
| p(0) | -1.104051 | 0.2027 | -5.45 | <.0001 | |********************************| | |
| p(1) | 0.082892 | 0.1257 | 0.66 | 0.5128 | | |*** | |
| p(2) | 0.263391 | 0.1381 | 1.91 | 0.0624 | | |********| |
| p(3) | -0.562556 | 0.2076 | -2.71 | 0.0093 | | ****************| | |
