The SSM Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set
State Space Model and NotationTypes of Sequence DataOverview of Model Specification SyntaxFiltering, Smoothing, Likelihood, and Structural Break DetectionEstimation of User-Specified Linear Combination of State ElementsContrasting PROC SSM with Other SAS Procedures Predefined Trend ModelsPredefined Structural ModelsCovariance ParameterizationMissing ValuesComputational IssuesDisplayed OutputODS Table NamesODS Graph NamesOUT= Data Set -
Examples
 Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis
Bivariate Basic Structural Model Panel Data: Random-Effects and Autoregressive ModelsBackcasting, Forecasting, and InterpolationLongitudinal Data: Smoothing of Repeated MeasuresA User-Defined Trend ModelModel with Multiple ARIMA ComponentsDynamic Factor ModelingDiagnostic Plots and Structural Break AnalysisLongitudinal Data: Variable Bandwidth SmoothingA Transfer Function Model for the Gas Furnace DataPanel Data: Dynamic Panel Model for the Cigar DataMultivariate Modeling: Long-Term Temperature TrendsBivariate Model: Sales of Mink and Muskrat FursFactor Model: Now-Casting the US EconomyLongitudinal Data: Lung Function Analysis - References
Suppose that a regression variable in a multivariate model affects two or more response variables. For example, suppose that
response variables y1 and y2 depend on a regression variable x. This dependence can be categorized as one of two types:
-
In the more common case, the regression coefficient of
xfory1and the regression coefficient ofxfory2are different. The relationship can be described as follows: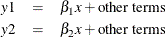
In the SSM procedure you can specify this type of relationship in two equivalent ways:
-
You can specify the variable
xin the MODEL statement fory1and specify the variablex_copy(a copy ofx) in the MODEL statement fory2as follows:x_copy = x; /* create a copy of x */ model y1 = x ...; model y2 = x_copy ...;
-
You can specify the variable
xin MODEL statements for bothy1andy2as follows:model y1 = x ...; model y2 = x ...;
This specification avoids creating
x_copy.
Of these two alternate ways, the first is preferred because
xandx_copycan then be unambiguously used in an EVAL statement to refer to the terms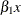 and
and 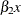 , respectively.
, respectively.
-
-
In the less common case,
y1andy2share a common regression coefficient.The relationship can be described as follows: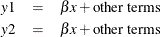
You can specify this type of relationship by placing the regression coefficient in the model state vector as follows:
state beta(1) T(I) A1(1) ; /* beta is a constant state */ comp xeffect = beta*(x) ; model y1 = xeffect ...; model y2 = xeffect ...;
Here the STATE statement defines
betaas a one-dimensional, time-invariant constant (because the transition matrix is identity, the disturbance covariance is 0 and the initial state is diffuse). Next, the COMP statement definesxeffectas the product betweenbetaand the variablex. Subsequently, bothy1andy2usexeffectin their respective MODEL statements.