The SSM Procedure

Example 27.1 Bivariate Basic Structural Model

This example illustrates how you can use the SSM procedure to analyze a bivariate time series. The following data set contains two variables, f_KSI and r_KSI, which are measured quarterly, starting the first quarter of 1969. The variable f_KSI represents the quarterly average of the log of the monthly totals of the front-seat passengers killed or seriously injured during the car accidents, and r_KSI represents a similar number for the rear-seat passengers. The data set has been extended at the end with eight missing values, which represent four quarters, to cause the SSM procedure to produce model forecasts for this span.

data seatBelt;
input f_KSI r_KSI @@;
label f_KSI = "Front Seat Passengers Injured--log scale";
label r_KSI = "Rear Seat Passengers Injured--log scale";
date = intnx( 'quarter', '1jan1969'd, _n_-1 );
format date YYQS.;
datalines;
    6.72417 5.64654  6.81728 6.06123  6.92382 6.18190
    6.92375 6.07763  6.84975 5.78544  6.81836 6.04644
    7.00942 6.30167  7.09329 6.14476  6.78554 5.78212
    6.86323 6.09520  6.99369 6.29507  6.98344 6.06194
    6.81499 5.81249  6.92997 6.10534  6.96356 6.21298
    7.02296 6.15261  6.76466 5.77967  6.95563 6.18993
    7.02016 6.40524  6.87849 6.06308  6.55966 5.66084
    6.73627 6.02395  6.91553 6.25736  6.83576 6.03535
    6.52075 5.76028  6.59860 5.91208  6.70597 6.08029
    6.75110 5.98833  6.53117 5.67676  6.52718 5.90572
    6.65963 6.01003  6.76869 5.93226  6.44483 5.55616
    6.62063 5.82533  6.72938 6.04531  6.82182 5.98277
    6.64134 5.76540  6.66762 5.91378  6.83524 6.13387
    6.81594 5.97907  6.60761 5.66838  6.62985 5.88151
    6.76963 6.06895  6.79927 6.01991  6.52728 5.69113
    6.60666 5.92841  6.72242 6.03111  6.76228 5.93898
    6.54290 5.72538  6.62469 5.92028  6.73415 6.11880
    6.74094 5.98009  6.46418 5.63517  6.61537 5.96040
    6.76185 6.15613  6.79546 6.04152  6.21529 5.70139
    6.27565 5.92508  6.40771 6.13903  6.37293 5.96883
    6.16445 5.77021  6.31242 6.05267  6.44414 6.15806
    6.53678 6.13404 . . . . . . . .
run;

These data have been analyzed in Durbin and Koopman (2001, chap. 9, sec. 3). The analysis presented here is similar. To simplify the illustration, the monthly data have been converted to quarterly data and two predictors (the number of kilometers traveled and the real price of petrol) are excluded from the analysis. You can also use PROC SSM to carry out the more elaborate analysis in Durbin and Koopman (2001).

One of the original reasons for studying these data was to assess the effect on f_KSI of the enactment of a seat-belt law in February 1983 that compelled the front seat passengers to wear seat belts. A simple graphical inspection of the data (not shown here) reveals that f_KSI and r_KSI do not show a pronounced upward or downward trend but do show seasonal variation, and that these two series seem to move together. Additional inspection also shows that the seasonal effect is relatively stable throughout the data span. These considerations suggest the following model for $\mb{y}$ = (f_KSI, r_KSI):

$\begin{equation*} \mb{y}_{t} = \binom {X_{t}}{0} \beta + \pmb {\mu }_{t} + \pmb {\zeta }_{t} + \pmb {\xi }_{t} \nonumber \end{equation*}$

All the terms on the right-hand side of this equation are assumed to be statistically independent. These terms are as follows:

The predictor 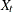$X_{t}$ (defined as Q1_83_Shift later in the program) denotes a variable that is 0 before the first quarter of 1983, and 1 thereafter.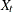 $X_{t}$ is supposed to affect only f_KSI (the first element of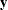 $\mb{y}$ ); it represents the enactment of the seat-belt law of 1983.
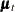$\pmb {\mu }_{t}$ denotes a bivariate random walk. It is supposed to capture the slowly changing level of the vector 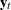$\mb{y}_{t}$ . To capture the fact that f_KSI and r_KSI move together (that is, they are co-integrated), the covariance of the disturbance term of this random walk is assumed to be of lower than full rank.
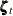$\pmb {\zeta }_{t}$ denotes a bivariate trigonometric seasonal term. In this model, it is taken to be fixed (that is, the seasonal effects do not change over time).
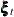$\pmb {\xi }_{t}$ denotes a bivariate white noise term, which captures the residual variation that is unexplained by the other terms in the model.

The preceding model is an example of a (bivariate) basic structural model (BSM). The following statements specify and fit this model to f_KSI and r_KSI:

 proc ssm data=seatBelt stateinfo;
    id date interval=quarter;
    Q1_83_Shift = (date >= '1jan1983'd);
    state error(2) type=WN cov(g) print=cov;
    component wn1 = error[1];
    component wn2 = error[2];
    state level(2) type=RW cov(rank=1) print=cov;
    component rw1 = level[1];
    component rw2 = level[2];
    state season(2) type=season(length=4);
    component s1 = season[1];
    component s2 = season[2];
    model f_KSI = Q1_83_Shift rw1 s1  wn1 / print=(smooth);
    model r_KSI = rw2 s2 wn2;
    eval f_KSI_sa = rw1 + Q1_83_Shift;
    output out=For1;
 run;

The PROC SSM statement specifies the input data set, seatBelt. The use of the STATEINFO option in the PROC SSM statement produces additional information about the model state vector and its diffuse initial state. The optional ID statement specifies an index variable, date. The INTERVAL=QUARTER option in the ID statement indicates that the measurements were collected on a quarterly basis. Next, a programming statement defines Q1_83_Shift, the predictor that represents the enactment of the seat-belt law of 1983. It is used later in the MODEL statement for f_KSI. Separate STATE statements specify the terms $\pmb {\mu }_{t}$ , $\pmb {\zeta }_{t}$ , and $\pmb {\xi }_{t}$ because they are statistically independent. Each model that governs them (white noise for $\pmb {\xi }_{t}$ , random walk for $\pmb {\mu }_{t}$ , and trigonometric seasonal for $\pmb {\zeta }_{t}$ ) can be specified by using the TYPE= option of the STATE statement. When you use the TYPE= option, you can use the COV option to specify the information about the disturbance covariance in the state transition equation. The other details, such as the transition matrix specification and the specification of $\mb{A}_{1}$ in the initial condition, are inferred from the TYPE= option. The use of PRINT=COV in the STATE statement causes the estimated disturbance covariance to be printed. For $\pmb {\xi }_{t}$ (a white noise), $\mb{A}_{1}$ is zero and $\mb{Q}_{t} = \mb{Q}$ for all $t \geq 1$ , where $\mb{Q}$ is specified by the COV option. For $\pmb {\mu }_{t}$ and $\pmb {\zeta }_{t}$ the initial condition is fully diffuse—that is, $\mb{A}_{1}$ is an identity matrix of appropriate order and $\mb{Q}_{1} = 0$ . The total diffuse dimension of this model, $(d+k)$ , is $9 = 8 + 1$ as a result of one predictor, Q1_83_Shift, and two fully diffuse state subsections, $\pmb {\mu }_{t}$ and $\pmb {\zeta }_{t}$ . The components in the model are defined by suitable linear combinations of these different state subsections. The program statements define the model as follows:

state error(2) type=WN cov(g); defines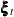 $\pmb {\xi }_{t}$ as a two-dimensional white noise, named error, with the covariance of general form. Then two COMPONENT statements define wn1 and wn2 as the first and second elements of error, respectively.
state level(2) type=RW cov(rank=1); defines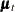 $\pmb {\mu }_{t}$ as a two-dimensional random walk, named level, with covariance of general form whose rank is restricted to 1. Then two COMPONENT statements define rw1 and rw2 as the first and second elements of level, respectively.
state season(2) type=season(length=4); defines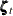 $\pmb {\zeta }_{t}$ as a two-dimensional trigonometric seasonal of season length 4, named season, with zero covariance—signified by the absence of the COV option. Then two COMPONENT statements define s1 and s2 as appropriate linear combinations of season so that s1 represents the seasonal for f_KSI and s2 represents the seasonal for r_KSI. Because TYPE=SEASON in the STATE statement, the COMPONENT statement appropriately interprets component s1 = season[1]; as s1 being a dot product: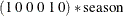 $( 1 \; 0 \; 0 \; 0 \; 1 \; 0) * \mr{season}$ . See the section Multivariate Season for more information.
model f_KSI = Q1_83_Shift rw1 s1 wn1; defines the model for f_KSI, and model r_KSI = rw2 s2 wn2; defines the model for r_KSI.

The SSM procedure fits the model and reports the parameter estimates, their approximate standard errors, and the likelihood-based goodness-of-fit measures by default. In order to output the one-step-ahead and full-sample estimates of the components in the model, you can either use the PRINT= options in the MODEL statement and the respective COMPONENT statements or you can specify an output data set in the OUTPUT statement. In addition, you can use the EVAL statement to define specific linear combinations of the underlying state that should also be estimated. The statement eval f_KSI_sa = rw1 + Q1_83_Shift; is an example of one such linear combination. It defines f_KSI_sa, a linear combination that represents the seasonal adjustment of f_KSI. The output data set, For1 (named in the OUTPUT statement) contains estimates of all the model components in addition to the estimate of f_KSI_sa.

The model summary table, shown in Output 27.1.1, provides basic model information, such as the dimension of the underlying state equation ( $m=10$ ), the diffuse dimension of the model ( $(d+k) = 9$ ), and the number of parameters (5) in the model parameter vector $\pmb {\theta }$ .

Output 27.1.1: Bivariate Basic Structural Model

The SSM Procedure

Model Summary
Model Property	Value
Number of Model Equations	2
State Dimension	10
Dimension of the Diffuse Initial Condition	9
Number of Parameters	5

Additional details about the role of different components in forming the model state and its diffuse initial condition are shown in Output 27.1.2 and Output 27.1.3. They show that the 10-dimensional model state vector is made up of subsections that are associated with error and level (each of dimension 2) and season (of dimension 6). Similarly, the nine-dimensional diffuse vector in the initial condition is made up of subsections that correspond to level, season, and the regression variable, Q1_83_Shift. Note that error does not contribute to the diffuse initial vector because it has a fully nondiffuse initial state.

Output 27.1.2: Bivariate Basic Structural Model State Vector Summary

State Vector Composition
Subsection	Dimension
error	2
level	2
season	6

Output 27.1.3: Bivariate Basic Structural Model Initial Diffuse State Vector Summary

Diffuse Initial State Composition
(Including Regressors)
Subsection	Dimension
level	2
season	6
Q1_83_Shift	1

The index variable information is shown in Output 27.1.4.

Output 27.1.4: Index Variable Information

ID Variable Information
Name	Start	End	Max Delta	Type
date	1969:1	1985:4	1	Regular

Output 27.1.5 provides simple summary information about the response variables. It shows that f_KSI and r_KSI have four missing values each and no induced missing values because the predictor in the model, Q1_83_Shift, has no missing values.

Output 27.1.5: Response Variable Summary

Response Variable Information
Name	Number of Observations			Minimum	Maximum	Mean	Std Deviation
Name	Total	Missing	Induced Missing	Minimum	Maximum	Mean	Std Deviation
f_KSI	68	4	0	6.16	7.09	6.71	0.206
r_KSI	68	4	0	5.56	6.41	5.97	0.186

The regression coefficient of Q1_83_Shift, shown in Output 27.1.6, is negative and is statistically significant. This is consistent with the expected drop in f_KSI after the enactment of the seat-belt law.

Output 27.1.6: Regression Coefficient of Q1_83_Shift

Regression Parameter Estimates
Response Variable	Regression Variable	Estimate	Standard Error	t Value	Pr > \|t\|
f_KSI	Q1_83_Shift	-0.408	0.0259	-15.74	<.0001

Output 27.1.7 shows the estimates of the elements of $\pmb {\theta }$ . The five parameters in $\pmb {\theta }$ correspond to unknown elements that are associated with the covariance matrices in the specifications of error and level. Whenever a covariance specification is of a general form and is not defined by a user-specified variable list, it is internally parameterized as a product of its Cholesky root: $\mr{Cov} = \mr{Root} \; \mr{Root}^{'}$ . This ensures that the resulting covariance is positive semidefinite. The Cholesky root is constrained to be lower triangular, with positive diagonal elements. If rank constraints (such as the rank-one constraint on the covariance in the specification of level) are imposed, the number of free parameters in the Cholesky factor is reduced appropriately. See the section Covariance Parameterization for more information. In view of these considerations, the five parameters in $\pmb {\theta }$ are a result of three parameters from the Cholesky root of error and two parameters that are associated with the Cholesky root of level.

Output 27.1.7: Parameter Estimates

Model Parameter Estimates
Component	Type	Parameter	Estimate	Standard Error
error	Disturbance Covariance	RootCov[1, 1]	0.0361	0.00736
error	Disturbance Covariance	RootCov[2, 1]	0.0338	0.01131
error	Disturbance Covariance	RootCov[2, 2]	0.0462	0.00470
level	Disturbance Covariance	RootCov[1, 1]	0.0375	0.00843
level	Disturbance Covariance	RootCov[2, 1]	0.0223	0.00569

Output 27.1.8 shows the resulting covariance estimate of error after multiplying the Cholesky factors.

Output 27.1.8: White Noise Covariance Estimate

Disturbance Covariance for error
	Col1	Col2
Row1	0.001307	0.001222
Row2	0.001222	0.003277

Similarly, Output 27.1.9 shows the covariance estimate of level disturbance. Note that because of the rank-one constraint, the determinant of this matrix is 0.

Output 27.1.9: Covariance Estimate of the Random Walk Disturbance

Disturbance Covariance for level
	Col1	Col2
Row1	0.001408	0.000837
Row2	0.000837	0.000497

Output 27.1.10 shows the likelihood computation summary. This table is produced by using the fitted model to carry out the filtering operation on the data. See the section Likelihood Computation and Model Fitting Phase for more information.

Output 27.1.10: Likelihood Computation Summary of the Fitted Model

Likelihood Computation Summary
Statistic	Value
Nonmissing Response Values Used	128
Estimated Parameters	5
Initialized Diffuse State Elements	9
Normalized Residual Sum of Squares	119.00001
Diffuse Log Likelihood	166.15755
Profile Log Likelihood	199.91165

The output data set, For1, specified in the OUTPUT statement contains one-step-ahead and full-sample estimates of all the model components and the user-specified components (defined by the EVAL statement). Their standard errors and the upper and lower confidence limits (by default, 95%) are also produced.

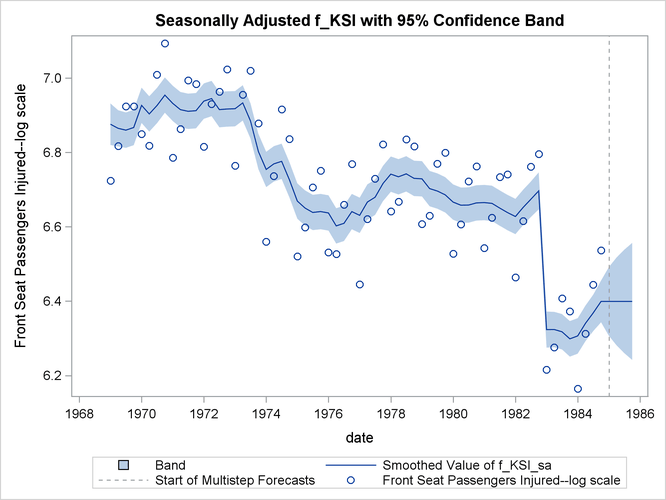
The following statements use the For1 data set to produce a time series plot of the seasonally adjusted f_KSI:

 proc sgplot data=For1;
    title "Seasonally Adjusted f_KSI with 95% Confidence Band";
    band x=date lower=smoothed_lower_f_KSI_sa
       upper=smoothed_upper_f_KSI_sa ;
    series x=date y=smoothed_f_KSI_sa;
    refline '1jan1985'd / axis=x lineattrs=(pattern=shortdash)
       LEGENDLABEL= "Start of Multistep Forecasts"
       name="Forecast Reference Line";
    scatter x=date y=f_KSI ;
 run;

The generated plot is shown in Output 27.1.11.

Output 27.1.11: Plot of Seasonally Adjusted f_KSI