Example 9.5 Categorical Linear Models
This example fits a linear model to a function of the response probabilities
where 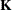 is a matrix that compares each response category to the last. Data are from Kastenbaum and Lamphiear (1959). First, the Grizzle-Starmer-Koch (1969) approach is used to obtain generalized least squares estimates of
is a matrix that compares each response category to the last. Data are from Kastenbaum and Lamphiear (1959). First, the Grizzle-Starmer-Koch (1969) approach is used to obtain generalized least squares estimates of 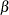 . These form the initial values for the Newton-Raphson solution for the maximum likelihood estimates. The CATMOD procedure
can also be used to analyze these binary data (see Cox (1970)). Here is the program.
. These form the initial values for the Newton-Raphson solution for the maximum likelihood estimates. The CATMOD procedure
can also be used to analyze these binary data (see Cox (1970)). Here is the program.
/* Categorical Linear Models */
/* by Least Squares and Maximum Likelihood */
/* CATLIN */
/* Input: */
/* n the s by p matrix of response counts */
/* x the s by r design matrix */
proc iml ;
start catlin;
/*---find dimensions---*/
s = nrow(n); /* number of populations */
r = ncol(n); /* number of responses */
q = r-1; /* number of function values */
d = ncol(x); /* number of design parameters */
qd = q*d; /* total number of parameters */
/*---get probability estimates---*/
rown = n[,+]; /* row totals */
pr = n/(rown*repeat(1,1,r)); /* probability estimates */
p = shape(pr[,1:q] ,0,1); /* cut and shaped to vector */
print "INITIAL PROBABILITY ESTIMATES" ,pr;
/* estimate by the GSK method */
/* function of probabilities */
f = log(p)-log(pr[,r])@repeat(1,q,1);
/* inverse covariance of f */
si = (diag(p)-p*p`)#(diag(rown)@repeat(1,q,q));
z = x@i(q); /* expanded design matrix */
h = z`*si*z; /* crossproducts matrix */
g = z`*si*f; /* cross with f */
beta = solve(h,g); /* least squares solution */
stderr = sqrt(vecdiag(inv(h))); /* standard errors */
run prob;
print ,"GSK ESTIMATES" , beta stderr ,pi;
/* iterations for ML solution */
crit = 1;
do it = 1 to 8 while(crit>.0005);/* iterate until converge*/
/* block diagonal weighting */
si = (diag(pi)-pi*pi`)#(diag(rown)@repeat(1,q,q));
g = z`*(rown@repeat(1,q,1)#(p-pi)); /* gradient */
h = z`*si*z; /* hessian */
delta = solve(h,g); /* solve for correction */
beta = beta+delta; /* apply the correction */
run prob; /* compute prob estimates */
crit = max(abs(delta)); /* convergence criterion */
end;
stderr = sqrt(vecdiag(inv(h))); /* standard errors */
print , "ML Estimates", beta stderr, pi;
print , "Iterations" it "Criterion" crit;
finish catlin;
/* subroutine to compute new prob estimates @ parameters */
start prob;
la = exp(x*shape(beta,0,q));
pi = la/((1+la[,+] )*repeat(1,1,q));
pi = shape(pi,0,1);
finish prob;
/*---prepare frequency data and design matrix---*/
n= { 58 11 05,
75 19 07,
49 14 10,
58 17 08,
33 18 15,
45 22 10,
15 13 15,
39 22 18,
04 12 17,
05 15 08}; /* frequency counts*/
x= { 1 1 1 0 0 0,
1 -1 1 0 0 0,
1 1 0 1 0 0,
1 -1 0 1 0 0,
1 1 0 0 1 0,
1 -1 0 0 1 0,
1 1 0 0 0 1,
1 -1 0 0 0 1,
1 1 -1 -1 -1 -1,
1 -1 -1 -1 -1 -1}; /* design matrix*/
run catlin;
The maximum likelihood estimates are shown in Output 9.5.1.
Output 9.5.1: Maximum Likelihood Estimates
| INITIAL PROBABILITY ESTIMATES |
| 0.7837838 |
0.1486486 |
0.0675676 |
| 0.7425743 |
0.1881188 |
0.0693069 |
| 0.6712329 |
0.1917808 |
0.1369863 |
| 0.6987952 |
0.2048193 |
0.0963855 |
| 0.5 |
0.2727273 |
0.2272727 |
| 0.5844156 |
0.2857143 |
0.1298701 |
| 0.3488372 |
0.3023256 |
0.3488372 |
| 0.4936709 |
0.278481 |
0.2278481 |
| 0.1212121 |
0.3636364 |
0.5151515 |
| 0.1785714 |
0.5357143 |
0.2857143 |
| 0.9454429 |
0.1290925 |
| 0.4003259 |
0.1284867 |
| -0.277777 |
0.1164699 |
| -0.278472 |
0.1255916 |
| 1.4146936 |
0.267351 |
| 0.474136 |
0.294943 |
| 0.8464701 |
0.2362639 |
| 0.1526095 |
0.2633051 |
| 0.1952395 |
0.2214436 |
| 0.0723489 |
0.2366597 |
| -0.514488 |
0.2171995 |
| -0.400831 |
0.2285779 |
| 0.7402867 |
| 0.1674472 |
| 0.7704057 |
| 0.1745023 |
| 0.6624811 |
| 0.1917744 |
| 0.7061615 |
| 0.2047033 |
| 0.516981 |
| 0.2648871 |
| 0.5697446 |
| 0.2923278 |
| 0.3988695 |
| 0.2589096 |
| 0.4667924 |
| 0.3034204 |
| 0.1320359 |
| 0.3958019 |
| 0.1651907 |
| 0.4958784 |
| 0.9533597 |
0.1286179 |
| 0.4069338 |
0.1284592 |
| -0.279081 |
0.1156222 |
| -0.280699 |
0.1252816 |
| 1.4423195 |
0.2669357 |
| 0.4993123 |
0.2943437 |
| 0.8411595 |
0.2363089 |
| 0.1485875 |
0.2635159 |
| 0.1883383 |
0.2202755 |
| 0.0667313 |
0.236031 |
| -0.527163 |
0.216581 |
| -0.414965 |
0.2299618 |
| 0.7431759 |
| 0.1673155 |
| 0.7723266 |
| 0.1744421 |
| 0.6627266 |
| 0.1916645 |
| 0.7062766 |
| 0.2049216 |
| 0.5170782 |
| 0.2646857 |
| 0.5697771 |
| 0.292607 |
| 0.3984205 |
| 0.2576653 |
| 0.4666825 |
| 0.3027898 |
| 0.1323243 |
| 0.3963114 |
| 0.165475 |
| 0.4972044 |
| Iterations |
3 |
Criterion |
0.0004092 |
![]() is a matrix that compares each response category to the last. Data are from Kastenbaum and Lamphiear (1959). First, the Grizzle-Starmer-Koch (1969) approach is used to obtain generalized least squares estimates of
is a matrix that compares each response category to the last. Data are from Kastenbaum and Lamphiear (1959). First, the Grizzle-Starmer-Koch (1969) approach is used to obtain generalized least squares estimates of ![]() . These form the initial values for the Newton-Raphson solution for the maximum likelihood estimates. The CATMOD procedure
can also be used to analyze these binary data (see Cox (1970)). Here is the program.
. These form the initial values for the Newton-Raphson solution for the maximum likelihood estimates. The CATMOD procedure
can also be used to analyze these binary data (see Cox (1970)). Here is the program.