Addition Operator: + :: SAS/IML(R) 12.1 User's Guide

Addition Operator: +

matrix1 + matrix2 ;

matrix + scalar ;

matrix + vector ;

The addition operator (+) computes a new matrix that contains elements that are the sums of the corresponding elements of matrix1 and matrix2. If matrix1 and matrix2 are both $n\times p$ matrices, then the addition operator adds the element in the th row and th column of the first matrix to the element in the th row and th column of the second matrix, for $i=1\ldots n, j=1\ldots p$ .

For example, the following statements add two matrices and store the result in the matrix c, shown in Figure 23.1:

a = {1 2,
     3 4};
b = {1 1,
     1 1};
c = a+b;
print c;

Figure 23.1: Sum of Two Matrices

c
2	3
4	5

You can also use the addition operator to conveniently add a value to each element of a matrix, to each column of a matrix, or to each row of a matrix.

When you use the matrix + scalar form, the scalar value is added to each element of the matrix.
When you use the matrix + vector form, the vector is added to each row or column of the 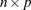$n\times p$ matrix.
- If you add an 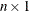$n\times 1$ column vector, each row of the vector is added to each row of the matrix.
- If you add a 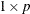$1\times p$ row vector, each column of the vector is added to each column of the matrix.

For example, you can obtain the same result as the previous example with any of the following statements:

c = a+1;
c = a+{1 1};
c = a+{1,1};

When an element of a matrix contains a missing value, the corresponding element of the sum is also a missing value.

You can also use the addition operator on character operands. In this case, the operator implements elementwise concatenation exactly as the CONCAT function.