Division Operator: / :: SAS/IML(R) 12.1 User's Guide

matrix1 / matrix2 ;

matrix / scalar ;

matrix / vector ;

The division operator (/) divides each element of matrix1 by the corresponding element of matrix2, producing a matrix of quotients.

You can also use the division operator to conveniently divide all elements of a matrix, each column of a matrix, or each row of a matrix.

When you use the matrix / scalar form, each element of the matrix is divided by the scalar value.
When you use the matrix / vector form, each row or column of the 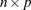$n\times p$ matrix is divided by a corresponding element of the vector.
- If you divide by an 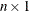$n\times 1$ column vector, each row of the matrix is divided by the corresponding row of the vector.
- If you divide by a 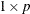$1\times p$ row vector, each column of the matrix is divided by the corresponding column of the vector.

When an element of a matrix contains a missing value, the corresponding element of the quotient is also a missing value.

If a divisor is zero, the operation displays a warning and assigns a missing value for the corresponding element in the result.

The following statements compute the matrices c and d, shown in Figure 23.10:

a = {1 2,
     3 4};
b = {5 6,
     7 8};
c = a/b;
d = a/4;
print c, d;

Figure 23.10: Results of Division

c
0.2	0.3333333
0.4285714	0.5

d
0.25	0.5
0.75	1