Multiplication Operator, Elementwise: # :: SAS/IML(R) 12.1 User's Guide

Multiplication Operator, Elementwise: #

matrix1 # matrix2 ;

matrix # scalar ;

matrix # vector ;

The elementwise multiplication operator (#) computes a new matrix with elements that are the products of the corresponding elements of matrix1 and matrix2.

For example, the following statements compute the matrix ab, shown in Figure 23.18:

a = {1 2,
     3 4};
b = {4 8,
     0 5};
ab = a#b;
print ab;

Figure 23.18: Results of Elementwise Multiplication

ab
4	16
0	20

In addition to multiplying matrices that have the same dimensions, you can use the elementwise multiplication operator to multiply a matrix and a scalar.

When either argument is a scalar, each element in matrix is multiplied by the scalar value.
When you use the matrix # vector form, each row or column of the 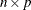$n\times p$ matrix is multiplied by a corresponding element of the vector.
- If you multiply by an 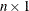$n\times 1$ column vector, each row of the matrix is multiplied by the corresponding row of the vector.
- If you multiply by a 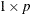$1\times p$ row vector, each column of the matrix is multiplied by the corresponding column of the vector.

For example, a $2 \times 3$ matrix can be multiplied on either side by a $2 \times 3$ , $1 \times 3$ , $2 \times 1$ , or $1 \times 1$ matrix. The following statements multiply the $2 \times 2$ matrix a by a column vector and a row vector. The results are shown in Figure 23.19.

c = {10, 100};         /* column vector */
r = {10 100};          /* row vector    */
ac = a#c;
ar = a#r;
print ac, ar;

Figure 23.19: Elementwise Multiplication with Vectors

ac
10	20
300	400

ar
10	200
30	400

Elementwise multiplication is also known as the Schur or Hadamard product. Elementwise multiplication (which uses the # operator) should not be confused with matrix multiplication (which uses the * operator).

When an element of a matrix contains a missing value, the corresponding element of the product is also a missing value.