DURATION Function :: SAS/IML(R) 12.1 User's Guide

DURATION Function

DURATION (times, flows, ytm) ;

The DURATION function returns a scalar value that represents the modified duration of a noncontingent cash flow. The arguments are as follows:

times: is an -dimensional column vector of times. The 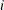th time corresponds to the time (often in years) until the 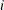th cash flow occurs. Elements should be nonnegative.
flows: is an -dimensional column vector of cash flows.
ytm: is the per-period yield-to-maturity of the cash-flow stream. This is a scalar and should be positive.

Duration of a security is generally defined as

$\begin{equation*} D =-\frac{ \frac{dP}{P} }{ dy } \end{equation*}$

In other words, it is the relative change in price for a unit change in yield. Since prices move in the opposite direction to yields, the sign change preserves positivity for convenience. With cash flows that are not yield-sensitive and the assumption of parallel shifts to a flat term structure, duration is given by

$\begin{equation*} D_\mr {mod}= \frac{ \sum _{k=1}^{K} t_ k \frac{ c(k) }{ (1+y)^{t_ k} } }{ P (1+y) } \end{equation*}$

where is the present value, is the per-period effective yield-to-maturity, is the number of cash flows, and the th cash flow is , periods from the present. This measure is referred to as modified duration to differentiate it from the Macaulay duration:

$\begin{equation*} D_\mr {Mac}= \frac{ \sum _{k=1}^{K} t_ k \frac{ c(k) }{ (1+y)^{t_ k} } }{ P } \end{equation*}$

This expression also reveals the reason for the name duration, since it is a present-value-weighted average of the duration (that is, timing) of all the cash flows and is hence an “average time-to-maturity” of the bond.

For example, consider the following statements:

times = 1;
flow = 10;
ytm = 0.1;
duration = duration(times, flow, ytm);
print duration;

Figure 23.100: Duration of a Cash Flow

duration
0.9090909