HADAMARD Function
HADAMARD (n, <, i> ) ;
The HADAMARD function returns a Hadamard matrix. The arguments to the HADAMARD function are as follows:
- n
-
specifies the order of the Hadamard matrix. You can specify that n is 1, 2, or a multiple of 4. Furthermore, n must satisfy at least one of the following conditions:
-
n
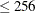
-
n – 1 is prime
-
(n
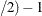 is prime and n
is prime and n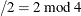
-
n
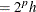 for some positives integers
for some positives integers 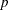 and
and 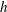 , and
, and 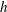 satisfies one of the preceding conditions
satisfies one of the preceding conditions
When any other n is specified, the HADAMARD function returns a zero.
-
- i
-
specifies the row number to return. When i is not specified or i is negative, the full Hadamard matrix is returned.
The HADAMARD function returns a Hadamard matrix, which is an ![]() matrix that consists entirely of the values 1 and –1. The columns of a Hadamard matrix are all orthogonal. Hadamard matrices
are frequently used to make orthogonal array experimental designs for two-level factors. For example, the following statements
create a
matrix that consists entirely of the values 1 and –1. The columns of a Hadamard matrix are all orthogonal. Hadamard matrices
are frequently used to make orthogonal array experimental designs for two-level factors. For example, the following statements
create a ![]() Hadamard matrix:
Hadamard matrix:
h = hadamard(12); print h[format=2.];
The output is shown in Figure 23.135. The first column is an intercept and the next 11 columns form an orthogonal array experimental design for 11 two-level factors
in 12 runs, ![]() .
.
Figure 23.135: A Hadamard Matrix
| h | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| 1 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 1 |
| 1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 |
| 1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 |
| 1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 |
| 1 | 1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 | 1 |
| 1 | 1 | 1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 | -1 |
| 1 | -1 | 1 | 1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 | -1 |
| 1 | -1 | -1 | 1 | 1 | 1 | -1 | 1 | 1 | -1 | 1 | -1 |
| 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 1 | 1 | -1 | 1 |
| 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 1 | 1 | -1 |
| 1 | -1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 1 | 1 |
To request the seventeenth row of a Hadamard matrix of order 448, use the following statement:
h17 = hadamard(448, 17);