IPF Call
CALL IPF (fit, status, dim, table, config <*>, initab <*>, mod ) ;
The IPF subroutine performs an iterative proportional fit of a contingency table. This is a standard statistical technique to obtain maximum likelihood estimates for cells under any hierarchical log-linear model. The algorithm is described in Bishop, Fienberg, and Holland (1975).
The arguments to the IPF subroutine are as follows:
- fit
-
is a returned matrix. The matrix fit contains an array of the estimates of the expected number in each cell under the model specified in config. This matrix conforms to table, meaning that it has the same dimensions and order of variables.
- status
-
is a returned matrix. The status argument is a row vector of length 3. status[1] is 0 if there is convergence to the desired accuracy, otherwise it is nonzero. status[2] is the maximum difference between estimates of the last two iterations of the IPF algorithm. status[3] is the number of iterations performed.
- dim
-
is an input matrix. If the problem contains
 variables, then dim is
variables, then dim is 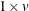 row vector. The value dim[i] is the number of possible levels for variable
row vector. The value dim[i] is the number of possible levels for variable 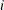 in a contingency table.
in a contingency table.
- table
-
is an input matrix that specifies an array of the number of observations at each level of each variable. Variables are nested across columns and then across rows.
- config
-
is an input matrix that specifies which marginal totals to fit. Each column of config specifies a distinct marginal in the model under consideration. Because the model is hierarchical, all subsets of specified marginals are included in fitting.
- initab
-
is an input matrix that specifies initial values for the iterative procedure. If you do not specify values, ones are used. For incomplete tables, initab is set to 1 if the cell is included in the design, and 0 if it is not.
- mod
-
is a two-element vector that specifies the stopping criteria. If mod= {MaxDev, MaxIter}, then the procedure iterates either until the maximum difference between estimates of the last two iterations is less than MaxDev or until MaxIter iterations are completed. Default values are MaxDev=0.25 and MaxIter=15.
The matrix table must conform in size to the contingency table as specified in dim. In particular, if table is ![]() , the product of the entries in dim must equal
, the product of the entries in dim must equal ![]() . Furthermore, there must be some integer
. Furthermore, there must be some integer ![]() such that the product of the first
such that the product of the first ![]() entries in dim equals
entries in dim equals ![]() . If you specify initab, then it must be the same size as table.
. If you specify initab, then it must be the same size as table.
Adjusting a Table from Marginals
A common use of the IPF subroutine is to adjust the entries of a table in order to fit a new set of marginals while retaining the interaction between cell entries.
Example 1: Adjusting Marital Status by Age
Bishop, Fienberg, and Holland (1975) present data from D. Friedlander that shows the distribution of women in England and Wales according to their marital status in 1957. One year later, new official marginal estimates were announced. The problem is to adjust the entries in the 1957 table so as to fit the new marginals while retaining the interaction between cells. This problem can arise when you have internal cells that are known from sampling a population and then get margins based on a complete census.
When you want to adjust an observed table of cell frequencies to a new set of margins, you must set the initab parameter to be the table of observed values. The new marginals are specified through the table argument. The particular cell values for table are not important, since only the marginals are used (the proportionality between cells is determined by initab).
There are two easy ways to create a table that contains given margins. Recall that a table of independent variables has an
expected cell value ![]() . Thus you could form a table with these cell entries. Another possibility is to use a “greedy algorithm” to assign as many of the marginals as possible to the first cell, then assign as many of the remaining marginals as possible
to the second cell, and so on until all of the marginals have been distributed. Both of these approaches are encapsulated
into modules in the following program:
. Thus you could form a table with these cell entries. Another possibility is to use a “greedy algorithm” to assign as many of the marginals as possible to the first cell, then assign as many of the remaining marginals as possible
to the second cell, and so on until all of the marginals have been distributed. Both of these approaches are encapsulated
into modules in the following program:
/* Return a table such that cell (i,j) has value
(sum of row i)(sum of col j)/(sum of all cells) */
start GetIndepTableFromMargins( bottom, side );
if bottom[+] ^= side[+] then do;
print "Marginal totals are not equal";
abort;
end;
table = side*bottom/side[+];
return (table);
finish;
/* Use a "greedy" algorithm to create a table whose
marginal totals match given marginal totals.
Margin1 is the vector of frequencies totaled down
each column. Margin1 means that
Variable 1 has NOT been summed over.
Margin2 is the vector of frequencies totaled across
each row. Margin2 means that Variable 2
has NOT been summed over.
After calling, use SHAPE to change the shape of
the returned argument. */
start GetGreedyTableFromMargins( Margin1, Margin2 );
/* copy arguments so they are not corrupted */
m1 = colvec(Margin1); /* colvec is in IMLMLIB */
m2 = colvec(Margin2);
if m1[+] ^= m2[+] then do;
print "Marginal totals are not equal";
abort;
end;
dim1 = nrow(m1);
dim2 = nrow(m2);
table = j(1,dim1*dim2,0);
/* give as much to cell (1,1) as possible,
then as much as remains to cell (1,2), etc,
until all the margins have been distributed */
idx = 1;
do i2 = 1 to dim2;
do i1 = 1 to dim1;
t = min(m1[i1],m2[i2]);
table[idx] = t;
idx = idx + 1;
m1[i1] = m1[i1]-t;
m2[i2] = m2[i2]-t;
end;
end;
return (table);
finish;
Mod = {0.01 15}; /* tighten stopping criterion */
Columns = {" Single" " Married" "Widow/Divorced"};
Rows = {"15 - 19" "20 - 24" "25 - 29" "30 - 34"
"35 - 39" "40 - 44" "45 - 49" "50 Or Over"};
/* Marital status has 3 levels. Age has 8 levels */
Dim = {3 8};
/* Use known distribution for start-up values */
IniTab = { 1306 83 0 ,
619 765 3 ,
263 1194 9 ,
173 1372 28 ,
171 1393 51 ,
159 1372 81 ,
208 1350 108 ,
1116 4100 2329 };
/* New marginal totals for age by marital status */
NewMarital = { 3988 11702 2634 };
NewAge = {1412,1402,1450,1541,1681,1532,1662,7644};
/* Create any table with these marginals */
Table = GetGreedyTableFromMargins(NewMarital, NewAge);
Table = shape(Table, nrow(IniTab), ncol(IniTab));
/* Consider all main effects */
Config = {1 2};
call ipf(Fit, Status, Dim, Table, Config, IniTab, Mod);
if Status[1] = 0 then
print "Known Distribution (1957)",
IniTab [colname=Columns rowname=Rows format=8.0],,
"Adjusted Estimates of Distribution (1958)",
Fit [colname=Columns rowname=Rows format=8.2];
else
print "IPF did not converge in "
(Status[3]) " iterations";
The results of this program are shown in Figure 23.149. The same results are obtained if the table parameter is formed by using the “independent algorithm.”
Figure 23.149: Iterative Proportional Fitting
| Known Distribution (1957) |
| IniTab | |||
|---|---|---|---|
| Single | Married | Widow/Divorced | |
| 15 - 19 | 1306 | 83 | 0 |
| 20 - 24 | 619 | 765 | 3 |
| 25 - 29 | 263 | 1194 | 9 |
| 30 - 34 | 173 | 1372 | 28 |
| 35 - 39 | 171 | 1393 | 51 |
| 40 - 44 | 159 | 1372 | 81 |
| 45 - 49 | 208 | 1350 | 108 |
| 50 Or Over | 1116 | 4100 | 2329 |
| Adjusted Estimates of Distribution (1958) |
| Fit | |||
|---|---|---|---|
| Single | Married | Widow/Divorced | |
| 15 - 19 | 1325.27 | 86.73 | 0.00 |
| 20 - 24 | 615.56 | 783.39 | 3.05 |
| 25 - 29 | 253.94 | 1187.18 | 8.88 |
| 30 - 34 | 165.13 | 1348.55 | 27.32 |
| 35 - 39 | 173.41 | 1454.71 | 52.87 |
| 40 - 44 | 147.21 | 1308.12 | 76.67 |
| 45 - 49 | 202.33 | 1352.28 | 107.40 |
| 50 Or Over | 1105.16 | 4181.04 | 2357.81 |
Example 2: Adjusting Votes by Region
A similar technique can be used to standardize data from raw counts into percentages. For example, consider data from a 1836 vote in the U.S. House of Representatives on a resolution that the House should adopt a policy of tabling all petitions for the abolition of slavery. Attitudes toward abolition were different among slaveholding states that would later secede from the Union (“the South”), slaveholding states that refused to secede (“the Border States”), and nonslaveholding states (“the North”).
The raw votes for the resolution are defined in the following statements. The data are hard to interpret because the margins are not homogeneous.
/* Yea Abstain Nay */
IniTab = { 61 12 60, /* North */
17 6 1, /* Border */
39 22 7 }; /* South */
Standardizing the data by specifying homogeneous margins reveals interactions and symmetry that were not apparent in the raw data. Suppose the margins are specified as follows:
NewVotes = {100 100 100};
NewSection = {100,100,100};
In this case, the program for marital status by age can be easily rewritten to adjust the votes into a standardized form. The resulting output is shown in Figure 23.150:
Figure 23.150: Standardizing Counts into Percentages
| Fit | |||
|---|---|---|---|
| Yea | Abstain | Nay | |
| North | 20.1 | 10.2 | 69.7 |
| Border | 47.4 | 42.8 | 9.8 |
| South | 32.5 | 47.0 | 20.5 |
Generating a Table with Given Marginals
The “greedy algorithm” presented in the Marital-Status-By-Age example can be extended in a natural way to the case where you have ![]() one-way marginals and want to form an
one-way marginals and want to form an ![]() -dimensional table. For example, a three-dimensional “greedy algorithm” would allocate the vector table as
-dimensional table. For example, a three-dimensional “greedy algorithm” would allocate the vector table as table=j(dim1*dim2*dim3,1,0); and have three nested loops as indicated in the following statements. Afterwards, the table parameter can be reshaped by using the SHAPE function.
do i3 = 1 to dim3;
do i2 = 1 to dim2;
do i1 = 1 to dim1;
t = min(m1[i1],m2[i2],m3[i3]);
table[idx] = t;
idx = idx + 1;
m1[i1] = m1[i1]-t;
m2[i2] = m2[i2]-t;
m3[i3] = m3[i3]-t;
end;
end;
end;
The idea of the “greedy algorithm” can be extended to marginals that are not one-way. For example, the following three-dimensional table is similar to one that appears in Christensen (1997) based on data from M. Rosenberg. The table presents data on a person’s self-esteem for people classified according to their religion and their father’s educational level.
|
Father’s Educational Level |
||||||
|
Self- |
Not HS |
HS |
Some |
Coll |
Post |
|
|
Religion |
Esteem |
Grad |
Grad |
Coll |
Grad |
Coll |
|
High |
575 |
388 |
100 |
77 |
51 |
|
|
Catholic |
||||||
|
Low |
267 |
153 |
40 |
37 |
19 |
|
|
High |
117 |
102 |
67 |
87 |
62 |
|
|
Jewish |
||||||
|
Low |
48 |
35 |
18 |
12 |
13 |
|
|
High |
359 |
233 |
109 |
197 |
90 |
|
|
Protestant |
||||||
|
Low |
159 |
173 |
47 |
82 |
32 |
|
Since the father’s education level is nested across columns, it is Variable 1 with levels that correspond to not finishing high school, graduating from high school, attending college, graduating from college, and attending graduate courses. The variable that varies the quickest across rows is Self-Esteem, so Self-Esteem is Variable 2 with values “High” and “Low.” The Religion variable is Variable 3 with values “Catholic,” “Jewish,” and “Protestant.”
The following program encodes this table by using the MARG call to compute a two-way marginal table by summing over the third variable, and a one-way marginal by summing over the first
two variables. Then a new table (NewTable) is created by applying the greedy algorithm to the two marginals. Finally, the marginals of NewTable are computed and compared with those of table.
dim={5 2 3};
table={
/* Father's Education:
NotHSGrad HSGrad Col ColGrad PostCol
Self-
Relig Esteem */
/* Cath- Hi */ 575 388 100 77 51,
/* olic Lo */ 267 153 40 37 19,
/* Jew- Hi */ 117 102 67 87 62,
/* ish Lo */ 48 35 18 12 13,
/* Prot- Hi */ 359 233 109 197 90,
/* estant Lo */ 159 173 47 82 32
};
config = { 1 3,
2 0 };
call marg(locmar, marginal, dim, table, config);
print locmar, marginal, table;
/* Examine marginals: The name indicates the
variable(s) that are NOT summed over.
The locmar variable tells where to index
into the marginal variable. */
Var12_Marg = marginal[1:(locmar[2]-1)];
Var12_Marg = shape(Var12_Marg,dim[2],dim[1]);
Var3_Marg = marginal[locMar[2]:ncol(marginal)];
NewTable = j(nrow(table),ncol(table),0);
/* give as much to cell (1,1,1) as possible,
then as much as remains to cell (1,1,2), etc,
until all the margins have been distributed. */
idx = 1;
do i3 = 1 to dim[3]; /* over Var3 */
do i2 = 1 to dim[2]; /* over Var2 */
do i1 = 1 to dim[1]; /* over Var1 */
/* Note Var12_Marg has Var1 varying across
the columns */
t = min(Var12_Marg[i2,i1],Var3_Marg[i3]);
NewTable[idx] = t;
idx = idx + 1;
Var12_Marg[i2,i1] = Var12_Marg[i2,i1]-t;
Var3_Marg[i3] = Var3_Marg[i3]-t;
end;
end;
end;
call marg(locmar, NewMarginal, dim, table, config);
maxDiff = abs(marginal-NewMarginal)[<>];
if maxDiff=0 then
print "Marginals are unchanged";
print NewTable;
Figure 23.151: Table with Given Marginals
| locmar | |
|---|---|
| 1 | 11 |
| marginal | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| COL1 | COL2 | COL3 | COL4 | COL5 | COL6 | COL7 | COL8 | COL9 | COL10 | COL11 | COL12 | COL13 | |
| ROW1 | 1051 | 723 | 276 | 361 | 203 | 474 | 361 | 105 | 131 | 64 | 1707 | 561 | 1481 |
| table | ||||
|---|---|---|---|---|
| 575 | 388 | 100 | 77 | 51 |
| 267 | 153 | 40 | 37 | 19 |
| 117 | 102 | 67 | 87 | 62 |
| 48 | 35 | 18 | 12 | 13 |
| 359 | 233 | 109 | 197 | 90 |
| 159 | 173 | 47 | 82 | 32 |
| Marginals are unchanged |
| NewTable | ||||
|---|---|---|---|---|
| 1051 | 656 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 67 | 276 | 218 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 143 | 203 |
| 474 | 361 | 105 | 131 | 64 |
Fitting a Log-Linear Model to a Table
A second common usage of the IPF algorithm is to hypothesize that the table of observations can be fitted by a model with known effects and to ask whether the observed values indicate that the model hypothesis can be accepted or should be rejected. In this usage, you normally do not specify the initab argument to the IPF subroutine (but see the comment on structural zeros in the section Additional Details).
Example 3: Food Illness
Korff, Taback, and Beard (1952) reported statistics related to the outbreak of food poisoning at a company picnic. A total of 304 people at the picnic were surveyed to determine who had eaten either of two suspect foods: potato salad and crabmeat. The predictor variables are whether the individual ate potato salad (Variable 1: “Yes” or “No”) and whether the person ate crabmeat (Variable 2: “Yes” or “No”). The response variable is whether the person was ill (Variable 3: “Ill” or “Not Ill”). The order of the variables is determined by the dim and table arguments to the IPF subroutine. The variables are nested across columns, then across rows.
|
Crabmeat: |
Y E S |
N O |
||||
|
Potato salad: |
Yes |
No |
Yes |
No |
||
|
Ill |
120 |
4 |
22 |
0 |
||
|
Not Ill |
80 |
31 |
24 |
23 |
||
The following program defines the variables and observations, and then fits three separate models. How well each model fits
the data is determined by computing a Pearson chi-square statistic ![]() , where the sum is over all cells,
, where the sum is over all cells, ![]() stands for the observed cell count, and
stands for the observed cell count, and ![]() stands for the fitted estimate. Other statistics, such as the likelihood-ratio chi-square statistic
stands for the fitted estimate. Other statistics, such as the likelihood-ratio chi-square statistic ![]() , could also be used.
, could also be used.
The program first fits a model that excludes the three-way interaction. The model fits well, so you can conclude that an association between illness and potato salad does not depend on whether an individual ate crabmeat. The next model excludes the interaction between potato salad and illness. This model is rejected with a large chi-square value, so the data support an association between potato salad and illness. The last model excludes the interaction between the crabmeat and the illness. This model fits moderately well.
/* Compute a chi-square score for a table of observed
values, given a table of expected values. Compare
this score to a chi-square value with given degrees
of freedom at 95% confidence level. */
start ChiSqTest( obs, model, degFreedom );
diff = (obs - model)##2 / model;
chiSq = diff[+];
chiSqCutoff = cinv(0.95, degFreedom);
print chiSq chiSqCutoff;
if chiSq > chiSqCutoff then
print "Reject hypothesis";
else
print "No evidence to reject hypothesis";
finish;
dim={2 2 2};
/* Crab meat: Y E S N O
Potato: Yes No Yes No */
table={ 120 4 22 0, /* Ill */
80 31 24 23 }; /* Not Ill */
crabmeat = " C R A B N O C R A B";
potato = {"YesPot" "NoPot" "YesPot" "NoPot"};
illness = {"Ill", "Not Ill"};
hypoth = "Hypothesis: no three-factor interaction";
config={1 1 2,
2 3 3};
call ipf(fit,status,dim,table,config);
print hypoth, "Fitted Model:",
fit[label=crabmeat colname=potato
rowname=illness format=6.2];
run ChiSqTest(table, fit, 1); /* 1 deg of freedom */
/* Test for interaction between Var 3 (Illness) and
Var 1 (Potato Salad) */
hypoth = "Hypothesis: no Illness-Potato Interaction";
config={1 2,
2 3};
call ipf(fit,status,dim,table,config);
print hypoth, "Fitted Model:",
fit[label=crabmeat colname=potato
rowname=illness format=6.2];
run ChiSqTest(table, fit, 2); /* 2 deg of freedom */
/* Test for interaction between Var 3 (Illness) and
Var 2 (Crab meat) */
hypoth = "Hypothesis: no Illness-Crab Interaction";
config={1 1,
2 3};
call ipf(fit,status,dim,table,config);
print hypoth, "Fitted Model:",
fit[label=crabmeat colname=potato
rowname=illness format=6.2];
run ChiSqTest(table, fit, 2); /* 2 deg of freedom */
Figure 23.152: Fitting Log-Linear Models
| hypoth |
|---|
| Hypothesis: no three-factor interaction |
| Fitted Model: |
| C R A B N O C R A B | ||||
|---|---|---|---|---|
| YesPot | NoPot | YesPot | NoPot | |
| Ill | 121.08 | 2.92 | 20.92 | 1.08 |
| Not Ill | 78.92 | 32.08 | 25.07 | 21.93 |
| chiSq | chiSqCutoff |
|---|---|
| 1.7021335 | 3.8414588 |
| No evidence to reject hypothesis |
| hypoth |
|---|
| Hypothesis: no Illness-Potato Interaction |
| Fitted Model: |
| C R A B N O C R A B | ||||
|---|---|---|---|---|
| YesPot | NoPot | YesPot | NoPot | |
| Ill | 105.53 | 18.47 | 14.67 | 7.33 |
| Not Ill | 94.47 | 16.53 | 31.33 | 15.67 |
| chiSq | chiSqCutoff |
|---|---|
| 44.344643 | 5.9914645 |
| Reject hypothesis |
| hypoth |
|---|
| Hypothesis: no Illness-Crab Interaction |
| Fitted Model: |
| C R A B N O C R A B | ||||
|---|---|---|---|---|
| YesPot | NoPot | YesPot | NoPot | |
| Ill | 115.45 | 2.41 | 26.55 | 1.59 |
| Not Ill | 84.55 | 32.59 | 19.45 | 21.41 |
| chiSq | chiSqCutoff |
|---|---|
| 5.0945132 | 5.9914645 |
| No evidence to reject hypothesis |
Additional Details
- Structural versus Random Zeros
-
In the Marital-Status-By-Age example, the initab argument contained a zero for the “15–19 and Widowed/Divorced” category. Because the initab parameter determines the proportionality between cells, the fitted model retains a zero in that category. By contrast, in the Food-Illness example, the table parameter contained a zero for number of illnesses observed among those who did not eat either crabmeat or potato salad. This is a sampling (random) zero. Some models preserve that zero; others do not. If your table has a structural zero (for example, the number of ovarian cancers observed among male patients), then you can use the initab parameter to preserve that zero. see Bishop, Fienberg, and Holland (1975) or the documentation for the CATMOD procedure in the SAS/STAT User's Guide for more information about structural zeros and incomplete tables.
- The config Parameter
-
The columns of this matrix specify which interaction effects should be included in the model. The following table specifies the model and the configuration parameter for common interactions for an
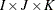 table in three dimensions. The so-called noncomprehensive models that do not include all variables (for example, config = {1}) are not listed in the table, but can be used. You can also specify combinations of main and interaction effects. For
example, config = {1 3, 2 0}) specifies all main effects and the 1-2 interaction. Bishop, Fienberg, and Holland (1975) and Christensen (1997) explain how to compute the degrees of freedom associated with any model. For models with structural zeros, computing the
degrees of freedom is complicated.
table in three dimensions. The so-called noncomprehensive models that do not include all variables (for example, config = {1}) are not listed in the table, but can be used. You can also specify combinations of main and interaction effects. For
example, config = {1 3, 2 0}) specifies all main effects and the 1-2 interaction. Bishop, Fienberg, and Holland (1975) and Christensen (1997) explain how to compute the degrees of freedom associated with any model. For models with structural zeros, computing the
degrees of freedom is complicated.
Model
config
Degrees of Freedom
No three-factor
{1 1 2,
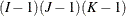
{2 3 3}
One two-factor absent
{1 2,
{3 3}
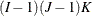
{1 2,
2 3}
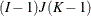
{1 1,
{2 3}
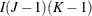
Two two-factor absent
{2, 3}
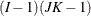
{1, 3}
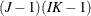
{1, 2}
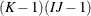
No two-factor
{1 2 3}
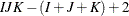
Saturated
{1,2,3}
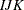
- The Shape of the table Parameter
-
Since variables are nested across columns and then across rows, any shape that conforms to the dim parameter is equivalent.
For example, the section Generating a Table with Given Marginals presents data on a person’s self-esteem for people classified according to their religion and their father’s educational level. To save space, the educational levels are subsequently denoted by labels that indicate the typical number of years spent in school: “<12,” “12,” “<16,” “16,” and “>16.”
The table would be encoded as follows:
dim={5 2 3}; table={ /* Father's Education: <12 12 <16 16 >16 Self- Relig Esteem */ /* Cath- Hi */ 575 388 100 77 51, /* olic Lo */ 267 153 40 37 19, /* Jew- Hi */ 117 102 67 87 62, /* ish Lo */ 48 35 18 12 13, /* Prot- Hi */ 359 233 109 197 90, /* estant Lo */ 159 173 47 82 32 };The same information for the same variables in the same order could also be encoded into an
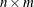 table in two other ways. Recall that the product of entries in dim is
table in two other ways. Recall that the product of entries in dim is 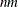 and that
and that 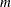 must equal the product of the first
must equal the product of the first 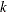 entries of dim for some
entries of dim for some 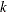 . For this example, the product of the entries in dim is
. For this example, the product of the entries in dim is 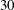 , and so the table must be
, and so the table must be 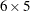 ,
, 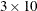 , or
, or 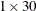 . The
. The 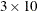 table is encoded as concatenating rows 1–2, 3–4, and 5–6 to produce the following:
table is encoded as concatenating rows 1–2, 3–4, and 5–6 to produce the following:
table={ /* Esteem: H I G H L O W */ /* <12 ... >16 <12 ... >16 */ 575 ... 51 267 ... 19, /* Catholic */ 117 ... 62 48 ... 13, /* Jewish */ 359 ... 90 159 ... 32 /* Protestant*/ };The
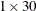 table is encoded by concatenating all rows, as follows:
table is encoded by concatenating all rows, as follows:
table={ /* CATHOLIC ... PROTESTANT High Low ... High Low <12 ... >16 <12 ... >16 ... <12 ... >16 <12 ... >16 */ 575 ... 51 267 ... 19 ... 359 ... 90 159 ... 32 };