MVE Call
CALL MVE (sc, coef, dist, opt, x <, s> ) ;
The MVE subroutine computes the robust estimation of multivariate location and scatter, defined by minimizing the volume of
an ellipsoid that contains ![]() points.
points.
The MVE subroutine computes the minimum volume ellipsoid estimator. These robust locations and covariance matrices can be used to detect multivariate outliers and leverage points. For this purpose, the MVE subroutine provides a table of robust distances.
In the following discussion, ![]() is the number of observations and
is the number of observations and ![]() is the number of regressors. The input arguments to the MVE subroutine are as follows:
is the number of regressors. The input arguments to the MVE subroutine are as follows:
- opt
-
refers to an options vector with the following components (missing values are treated as default values):
- opt[1]
-
specifies the amount of printed output. Higher option values request additional output and include the output of lower values.
- 0
-
prints no output except error messages.
- 1
-
prints most of the output.
- 2
-
additionally prints case numbers of the observations in the best subset and some basic history of the optimization process.
- 3
-
additionally prints how many subsets result in singular linear systems.
The default is opt[1]=0.
- opt[2]
-
specifies whether the classical, initial, and final robust covariance matrices are printed. The default is opt[2]=0. The final robust covariance matrix is always returned in coef.
- opt[3]
-
specifies whether the classical, initial, and final robust correlation matrices are printed or returned. The default is opt[3]=0.
- 0
-
does not return or print.
- 1
-
prints the robust correlation matrix.
- 2
-
returns the final robust correlation matrix in coef.
- 3
-
prints and returns the final robust correlation matrix.
- opt[4]
-
specifies the quantile
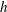 used in the objective function. The default is opt[5]=
used in the objective function. The default is opt[5]= ![$h = \left[\frac{N+n+1}{2}\right]$](images/imlug_langref0954.png) . If the value of
. If the value of 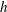 is specified outside the range
is specified outside the range 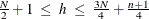 , it is reset to the closest boundary of this region.
, it is reset to the closest boundary of this region.
- opt[5]
-
specifies the number
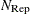 of subset generations. This option is the same as described previously for the LMS and LTS subroutines. Due to computer time
restrictions, not all subset combinations can be inspected for larger values of
of subset generations. This option is the same as described previously for the LMS and LTS subroutines. Due to computer time
restrictions, not all subset combinations can be inspected for larger values of 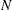 and
and  . If opt[5] is zero or missing, the default number of subsets is taken from the following table.
. If opt[5] is zero or missing, the default number of subsets is taken from the following table.
n
1
2
3
4
5
6
7
8
9
10
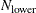
500
50
22
17
15
14
0
0
0
0
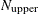
1414
182
71
43
32
27
24
23
22
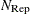
500
1000
1500
2000
2500
3000
3000
3000
3000
3000
n
11
12
13
14
15
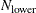
0
0
0
0
0
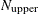
22
22
22
23
23
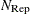
3000
3000
3000
3000
3000
If the number of cases (observations)
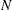 is smaller than
is smaller than 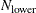 , as given in the table, then all possible subsets are used; otherwise,
, as given in the table, then all possible subsets are used; otherwise, 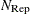 subsets are chosen randomly. This means that an exhaustive search is performed for opt[5]
subsets are chosen randomly. This means that an exhaustive search is performed for opt[5]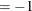 . If
. If 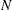 is larger than
is larger than 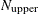 , a note is printed in the log file that indicates how many subsets exist.
, a note is printed in the log file that indicates how many subsets exist.
- x
-
refers to an
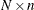 matrix
matrix 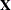 of regressors. Missing values are not permitted in
of regressors. Missing values are not permitted in  .
.
- s
-
refers to an
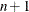 vector that contains
vector that contains 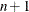 observation numbers of a subset for which the objective function should be evaluated, where
observation numbers of a subset for which the objective function should be evaluated, where  is the number of parameters. In other words, the MVE algorithm computes the minimum volume of the ellipsoid that contains
the observation numbers contained in
is the number of parameters. In other words, the MVE algorithm computes the minimum volume of the ellipsoid that contains
the observation numbers contained in  .
.
The MVE subroutine returns the following values:
- sc
-
is a column vector that contains the following scalar information:
- sc[1]
-
the quantile
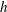 used in the objective function
used in the objective function
- sc[2]
-
number of subsets generated
- sc[3]
-
number of subsets with singular linear systems
- sc[4]
-
number of nonzero weights
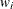
- sc[5]
-
lowest value of the objective function
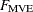 attained (volume of smallest ellipsoid found)
attained (volume of smallest ellipsoid found)
- sc[6]
-
Mahalanobis-like distance used in the computation of the lowest value of the objective function
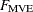
- sc[7]
-
the cutoff value used for the outlier decision
- coef
-
is a matrix with
 columns that contains the following results in its rows:
columns that contains the following results in its rows:
- coef[1,]
-
location of ellipsoid center
- coef[2,]
-
eigenvalues of final robust scatter matrix
- coef[3:2+n,]
-
the final robust scatter matrix for opt[2]=1 or opt[2]=3
- coef[2+n+1:2+2n,]
-
the final robust correlation matrix for opt[3]=1 or opt[3]=3
- dist
-
is a matrix with
 columns that contains the following results in its rows:
columns that contains the following results in its rows:
- dist[1,]
-
Mahalanobis distances
- dist[2,]
-
robust distances based on the final estimates
- dist[3,]
-
weights (1 for small robust distances; 0 for large robust distances)
Example
Consider results for Brownlee (1965) stackloss data. The three explanatory variables correspond to measurements for a plant that oxidizes ammonia to nitric acid on 21 consecutive days:
-
 air flow to the plant
air flow to the plant
-
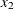 cooling water inlet temperature
cooling water inlet temperature
-
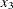 acid concentration
acid concentration
The response variable ![]() contains the permillage of ammonia lost (stackloss). These data are also given by Rousseeuw and Leroy (1987).
contains the permillage of ammonia lost (stackloss). These data are also given by Rousseeuw and Leroy (1987).
/* X1 X2 X3 Y Stackloss data */
aa = { 1 80 27 89 42,
1 80 27 88 37,
1 75 25 90 37,
1 62 24 87 28,
1 62 22 87 18,
1 62 23 87 18,
1 62 24 93 19,
1 62 24 93 20,
1 58 23 87 15,
1 58 18 80 14,
1 58 18 89 14,
1 58 17 88 13,
1 58 18 82 11,
1 58 19 93 12,
1 50 18 89 8,
1 50 18 86 7,
1 50 19 72 8,
1 50 19 79 8,
1 50 20 80 9,
1 56 20 82 15,
1 70 20 91 15 };
Rousseeuw and Leroy (1987) cite a large number of papers where this data set was analyzed and state that most researchers “concluded that observations 1, 3, 4, and 21 were outliers”; some people also reported observation 2 as an outlier.
By default, subroutine MVE chooses only 2,000 randomly selected subsets in its search. There are in total 5,985 subsets of 4 cases out of 21 cases, as shown in Figure 23.193, which is produced by the following statements:
a = aa[, 2:4]; opt = j(8, 1, .); opt[1] = 2; /* ipri */ opt[2] = 1; /* pcov: print COV */ opt[3] = 1; /* pcor: print CORR */ opt[5] = -1; /* nrep: use all subsets */ call mve(sc, xmve, dist, opt, a);
The first part of the output (Figure 23.193) shows the classical scatter and correlation matrix, along with the means of each variable.
Figure 23.193: Classical Estimates of Scatter and Location
| Classical Covariance Matrix | |||
|---|---|---|---|
| VAR1 | VAR2 | VAR3 | |
| VAR1 | 84.057142857 | 22.657142857 | 24.571428571 |
| VAR2 | 22.657142857 | 9.9904761905 | 6.6214285714 |
| VAR3 | 24.571428571 | 6.6214285714 | 28.714285714 |
| Classical Correlation Matrix | |||
|---|---|---|---|
| VAR1 | VAR2 | VAR3 | |
| VAR1 | 1 | 0.781852333 | 0.5001428749 |
| VAR2 | 0.781852333 | 1 | 0.3909395378 |
| VAR3 | 0.5001428749 | 0.3909395378 | 1 |
| Classical Mean | |
|---|---|
| VAR1 | 60.428571429 |
| VAR2 | 21.095238095 |
| VAR3 | 86.285714286 |
The second part of the output (Figure 23.194) shows the results of the optimization (complete subset sampling):
Figure 23.194: Subset Sampling and Optimal Subset
| Subset | Singular | Best Criterion |
Percent |
|---|---|---|---|
| 1497 | 22 | 253.312431 | 25 |
| 2993 | 46 | 224.084073 | 50 |
| 4489 | 77 | 165.830053 | 75 |
| 5985 | 156 | 165.634363 | 100 |
| Observations of Best Subset | |||
|---|---|---|---|
| 7 | 10 | 14 | 20 |
| Initial MVE Location Estimates |
|
|---|---|
| VAR1 | 58.5 |
| VAR2 | 20.25 |
| VAR3 | 87 |
| Initial MVE Scatter Matrix | |||
|---|---|---|---|
| VAR1 | VAR2 | VAR3 | |
| VAR1 | 34.829014749 | 28.413143611 | 62.32560534 |
| VAR2 | 28.413143611 | 38.036950318 | 58.659393261 |
| VAR3 | 62.32560534 | 58.659393261 | 267.63348175 |
The third part of the output (Figure 23.195) shows the optimization results after local improvement:
Figure 23.195: Robust Estimates of Scatter and Location
| Robust MVE Location Estimates | |
|---|---|
| VAR1 | 56.705882353 |
| VAR2 | 20.235294118 |
| VAR3 | 85.529411765 |
| Robust MVE Scatter Matrix | |||
|---|---|---|---|
| VAR1 | VAR2 | VAR3 | |
| VAR1 | 23.470588235 | 7.5735294118 | 16.102941176 |
| VAR2 | 7.5735294118 | 6.3161764706 | 5.3676470588 |
| VAR3 | 16.102941176 | 5.3676470588 | 32.389705882 |
| Eigenvalues of Robust Scatter Matrix |
|
|---|---|
| VAR1 | 46.597431018 |
| VAR2 | 12.155938483 |
| VAR3 | 3.423101087 |
| Robust Correlation Matrix | |||
|---|---|---|---|
| VAR1 | VAR2 | VAR3 | |
| VAR1 | 1 | 0.6220269501 | 0.5840361335 |
| VAR2 | 0.6220269501 | 1 | 0.375278187 |
| VAR3 | 0.5840361335 | 0.375278187 | 1 |
The final output (Figure 23.196) presents a table that contains the classical Mahalanobis distances, the robust distances, and the weights that identify
the outlying observations (that is leverage points when explaining ![]() with these three regressor variables):
with these three regressor variables):
Figure 23.196: Distances and Weights
| Classical Distances and Robust (Rousseeuw) Distances | |||
|---|---|---|---|
| Unsquared Mahalanobis Distance and | |||
| Unsquared Rousseeuw Distance of Each Observation | |||
| N | Mahalanobis Distances | Robust Distances | Weight |
| 1 | 2.253603 | 5.528395 | 0 |
| 2 | 2.324745 | 5.637357 | 0 |
| 3 | 1.593712 | 4.197235 | 0 |
| 4 | 1.271898 | 1.588734 | 1.000000 |
| 5 | 0.303357 | 1.189335 | 1.000000 |
| 6 | 0.772895 | 1.308038 | 1.000000 |
| 7 | 1.852661 | 1.715924 | 1.000000 |
| 8 | 1.852661 | 1.715924 | 1.000000 |
| 9 | 1.360622 | 1.226680 | 1.000000 |
| 10 | 1.745997 | 1.936256 | 1.000000 |
| 11 | 1.465702 | 1.493509 | 1.000000 |
| 12 | 1.841504 | 1.913079 | 1.000000 |
| 13 | 1.482649 | 1.659943 | 1.000000 |
| 14 | 1.778785 | 1.689210 | 1.000000 |
| 15 | 1.690241 | 2.230109 | 1.000000 |
| 16 | 1.291934 | 1.767582 | 1.000000 |
| 17 | 2.700016 | 2.431021 | 1.000000 |
| 18 | 1.503155 | 1.523316 | 1.000000 |
| 19 | 1.593221 | 1.710165 | 1.000000 |
| 20 | 0.807054 | 0.675124 | 1.000000 |
| 21 | 2.176761 | 3.657281 | 0 |
| MinRes | 1st Qu. | Median | Mean | 3rd Qu. | MaxRes |
|---|---|---|---|---|---|
| 0.6751244996 | 1.5084120761 | 1.7159242054 | 2.2282960174 | 2.0831826658 | 5.6373573538 |