ORTVEC Call
CALL ORTVEC (w, r, rho, lindep, v <, q> ) ;
The ORVEC subroutine provides columnwise orthogonalization and stepwise QR decomposition by using the Gram-Schmidt process.
The ORTVEC subroutine returns the following values:
- w
-
is an
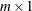 vector. If the Gram-Schmidt process converges (lindep=0), w is orthonormal to the columns of
vector. If the Gram-Schmidt process converges (lindep=0), w is orthonormal to the columns of 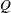 , which is assumed to have
, which is assumed to have 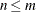 (nearly) orthonormal columns. If the Gram-Schmidt process does not converge (lindep=1), w is a vector of missing values. For stepwise QR decomposition, w is the
(nearly) orthonormal columns. If the Gram-Schmidt process does not converge (lindep=1), w is a vector of missing values. For stepwise QR decomposition, w is the 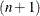 th orthogonal column of the matrix
th orthogonal column of the matrix 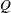 . If the q argument is not specified, w is the normalized value of the vector v,
. If the q argument is not specified, w is the normalized value of the vector v,
![\[ w = \frac{v}{\sqrt {v^{\prime } v}} \]](images/imlug_langref1137.png)
- r
-
is a
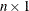 vector. If the Gram-Schmidt process converges (lindep=0), r contains Fourier coefficients. If the Gram-Schmidt process does not converge (lindep=1), r is a vector of missing values. If the q argument is not specified, r is a vector with zero dimension. For stepwise QR decomposition, r contains the
vector. If the Gram-Schmidt process converges (lindep=0), r contains Fourier coefficients. If the Gram-Schmidt process does not converge (lindep=1), r is a vector of missing values. If the q argument is not specified, r is a vector with zero dimension. For stepwise QR decomposition, r contains the  upper triangular elements of the
upper triangular elements of the 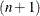 th column of
th column of 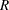 .
.
- rho
-
is a scalar value. If the Gram-Schmidt process converges (lindep=0), rho specifies the distance from w to the range of
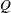 . Even if the Gram-Schmidt process converges, if rho is sufficiently small, the vector v can be linearly dependent on the columns of
. Even if the Gram-Schmidt process converges, if rho is sufficiently small, the vector v can be linearly dependent on the columns of 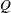 . If the Gram-Schmidt process does not converge (lindep=1), rho is set to 0. For stepwise QR decomposition, rho contains the diagonal element of the
. If the Gram-Schmidt process does not converge (lindep=1), rho is set to 0. For stepwise QR decomposition, rho contains the diagonal element of the 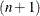 th column of
th column of 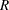 . In formulas, the value rho is denoted by
. In formulas, the value rho is denoted by 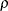 .
.
- lindep
-
returns a value of 1 if the Gram-Schmidt process does not converge in 10 iterations. A value of 1 often indicates that the input vector v is linearly dependent on the
 columns of the input matrix
columns of the input matrix 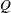 . In that case, rho is set to 0, and the results w and r contain missing values. If lindep=0, the Gram-Schmidt process did converge, and the results w, r, and rho are computed.
. In that case, rho is set to 0, and the results w and r contain missing values. If lindep=0, the Gram-Schmidt process did converge, and the results w, r, and rho are computed.
The input arguments to the ORTVEC subroutine are as follows:
- v
-
specifies an
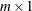 vector v that is to be orthogonalized to the
vector v that is to be orthogonalized to the  columns of
columns of 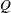 . For stepwise QR decomposition of a matrix, v is the
. For stepwise QR decomposition of a matrix, v is the 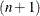 th matrix column before its orthogonalization.
th matrix column before its orthogonalization.
- q
-
specifies an optional
 matrix
matrix 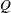 that is assumed to have
that is assumed to have 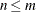 (nearly) orthonormal columns. Thus, the
(nearly) orthonormal columns. Thus, the 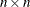 matrix
matrix 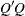 should approximate the identity matrix. The column orthonormality assumption is not tested in the ORTVEC call. If it is violated,
the results are not predictable. The argument q can be omitted or can have zero rows and columns. For stepwise QR decomposition of a matrix, q contains the first
should approximate the identity matrix. The column orthonormality assumption is not tested in the ORTVEC call. If it is violated,
the results are not predictable. The argument q can be omitted or can have zero rows and columns. For stepwise QR decomposition of a matrix, q contains the first  matrix columns that are already orthogonal.
matrix columns that are already orthogonal.
The relevant formula for the ORTVEC subroutine is
|
|
In the formula, if the ![]() matrix
matrix ![]() has
has ![]() (nearly) orthonormal columns, the vector v is orthogonal to the columns of
(nearly) orthonormal columns, the vector v is orthogonal to the columns of ![]() and
and ![]() is the distance from w to the range of
is the distance from w to the range of ![]() .
.
There are two special cases:
-
If
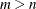 , ORTVEC normalizes the result w, so that w
, ORTVEC normalizes the result w, so that w w
w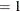 .
.
-
If
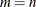 , the output vector w is the null vector.
, the output vector w is the null vector.
The case ![]() is not possible since
is not possible since ![]() is assumed to have
is assumed to have ![]() (nearly) orthonormal columns.
(nearly) orthonormal columns.
To initialize a stepwise QR decomposition, the ORTVEC subroutine can be called to normalize v only (that is, to compute ![]() and
and ![]() ). There are two ways to accomplish this:
). There are two ways to accomplish this:
-
Omit the last argument q, as in
call ortvec(w,r,rho,lindep,v);. -
Provide a matrix q with zero rows and columns (for example, by using
q={}).
In both cases, r is a column vector with zero rows.
The ORTVEC subroutine is useful for the following applications:
-
performing stepwise QR decomposition. Compute
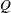 and
and 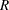 , so that
, so that 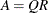 , where
, where 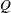 is column orthonormal,
is column orthonormal, 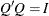 , and
, and 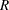 is upper triangular. The
is upper triangular. The 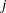 th step is applied to the
th step is applied to the 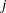 th column, v, of
th column, v, of 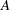 , and it computes the
, and it computes the 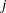 th column w of
th column w of 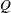 and the
and the 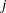 th column,
th column, 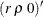 , of
, of 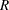 .
.
-
computing the
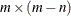 null space matrix,
null space matrix, 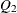 , that corresponds to an
, that corresponds to an  range space matrix,
range space matrix, 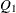
 , by the following stepwise process:
, by the following stepwise process:
-
Set
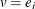 (where
(where 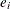 is the
is the 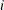 th unit vector) and try to make it orthogonal to all column vectors of
th unit vector) and try to make it orthogonal to all column vectors of 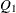 and the already generated
and the already generated 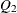 .
.
-
If the subroutine is successful, append w to
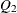 ; otherwise, try
; otherwise, try 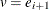 .
.
-
The ![]() matrix
matrix ![]() contains the unit vectors
contains the unit vectors ![]() , and
, and ![]() . The column vector v is pairwise linearly independent with the three columns of
. The column vector v is pairwise linearly independent with the three columns of ![]() . As expected, the ORTVEC subroutine computes the vector w as the unit vector
. As expected, the ORTVEC subroutine computes the vector w as the unit vector ![]() with
with ![]() and
and ![]() .
.
q = { 1 0 0,
0 0 0,
0 1 0,
0 0 1 };
v = { 1, 1, 1, 1 };
call ortvec(w,u,rho,lindep,v,q);
print rho u w;
Figure 23.232: Matrix Orthogonalization
| rho | u | w |
|---|---|---|
| 1 | 1 | 0 |
| 1 | 1 | |
| 1 | 0 | |
| 0 |
Stepwise QR Decomposition Example
You can perform the QR decomposition of the linearly independent columns of an ![]() matrix
matrix ![]() with the following statements:
with the following statements:
a = {1 2 1,
2 4 2,
1 4 -1,
1 0 3}; /* use any matrix A */
nind = 0; ndep = 0; dmax = 0.;
n = ncol(a); m = nrow(a); ind = j(1,n,0);
free q;
do j = 1 to n;
v = a[ ,j];
call ortvec(w,u,rho,lindep,v,q);
aro = abs(rho);
if aro > dmax then dmax = aro;
if aro <= 1.e-10 * dmax then lindep = 1;
if lindep = 0 then do;
nind = nind + 1;
q = q || w;
if nind = n then r = r || (u // rho);
else r = r || (u // rho // j(n-nind,1,0.));
end;
else do;
print "Column " j " is linearly dependent.";
ndep = ndep + 1; ind[ndep] = j;
end;
end;
print q r;
Figure 23.233: QR Decomposition of Independent Columns
| q | r | ||
|---|---|---|---|
| 0.3779645 | 0 | 2.6457513 | 5.2915026 |
| 0.7559289 | 0 | 0 | 2.8284271 |
| 0.3779645 | 0.7071068 | 0 | 0 |
| 0.3779645 | -0.707107 |
Next, process the remaining (dependent) columns of ![]() :
:
do j = 1 to ndep;
k = ind[ndep-j+1];
v = a[ ,k];
call ortvec(w,u,rho,lindep,v,q);
if lindep = 0 then do;
nind = nind + 1;
q = q || w;
if nind = n then r = r || (u // rho);
else r = r || (u // rho // j(n-nind,1,0.));
end;
end;
print q r;
Figure 23.234: QR Decomposition of Dependent Columns
| q | r | ||||
|---|---|---|---|---|---|
| 0.3779645 | 0 | -0.239046 | 2.6457513 | 5.2915026 | 2.6457513 |
| 0.7559289 | 0 | -0.478091 | 0 | 2.8284271 | -2.828427 |
| 0.3779645 | 0.7071068 | 0.5976143 | 0 | 0 | 1.327E-16 |
| 0.3779645 | -0.707107 | 0.5976143 | |||
You can also use the ORTVEC subroutine to compute the null space in the last columns of ![]() :
:
do i = 1 to m;
if nind < m then do;
v = j(m,1,0.); v[i] = 1.;
call ortvec(w,u,rho,lindep,v,q);
aro = abs(rho);
if aro > dmax then dmax = aro;
if aro <= 1.e-10 * dmax then lindep = 1;
if lindep = 0 then do;
nind = nind + 1;
q = q || w;
end;
else print "Unit vector" i "linearly dependent.";
end;
end;
if nind < m then do;
print "This is theoretically not possible.";
end;
print q;
Figure 23.235: Final Orthogonal Matrix
| q | |||
|---|---|---|---|
| 0.3779645 | 0 | -0.239046 | 0.8944272 |
| 0.7559289 | 0 | -0.478091 | -0.447214 |
| 0.3779645 | 0.7071068 | 0.5976143 | 0 |
| 0.3779645 | -0.707107 | 0.5976143 | -3.1E-17 |
In the example, if you define ![]() to be the last two columns of
to be the last two columns of ![]() , then
, then ![]() .
.