Getting Started :: SAS/IML(R) 12.1 User's Guide

Getting Started

Stationary VAR Process
Nonstationary VAR Process

Stationary VAR Process

Generate the process following the first-order stationary vector autoregressive model with zero mean

$\displaystyle \mb {y}_{t} = \left( \begin{array}{rr} 1.2 & -0.5 \\ 0.6 & 0.3 \\ \end{array} \right) \mb {y}_{t-1} + {\mbox{\boldmath $\epsilon $}}_ t ~ ~ \textrm{with}~ ~ \Sigma = \left( \begin{array}{rr} 1.0 & 0.5 \\ 0.5 & 1.25 \\ \end{array} \right)$

The following statements compute the roots of characteristic function, compute the five lags of cross-covariance matrices, generate 100 observations simulated data, and evaluate the log-likelihood function of the VAR(1) model:

proc iml;
/* Stationary VAR(1) model */
sig = {1.0  0.5, 0.5 1.25};
phi = {1.2 -0.5, 0.6 0.3};
call varmasim(yt,phi) sigma=sig n=100 seed=3243; 
call vtsroot(root,phi); 
print root;
call varmacov(crosscov,phi) sigma=sig lag=5; 
lag = {'0','','1','','2','','3','','4','','5',''}; 
print lag crosscov;
call varmalik(lnl,yt,phi) sigma=sig; 
print lnl;

Figure 13.29: Plot of Generated VAR(1) Process (VARMASIM)

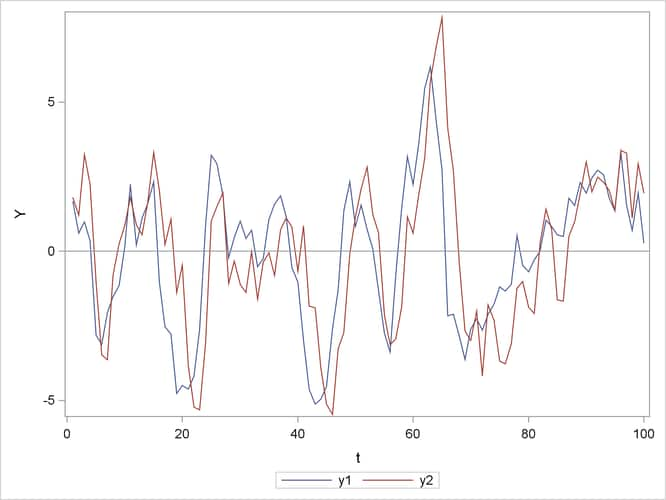
The stationary VAR(1) processes show in Figure 13.29.

Figure 13.30: Roots of VAR(1) Model (VTSROOT)

root
0.75	0.3122499	0.8124038	0.3945069	22.603583
0.75	-0.31225	0.8124038	-0.394507	-22.60358

In Figure 13.30, the first column is the real part () of the root of the characteristic function and the second one is the imaginary part (). The third column is the modulus, the squared root of . The fourth column is $Tan^{-1}(I/R)$ and the last one is the degree. Since moduli are less than one from the third column, the series is obviously stationary.

Figure 13.31: Cross-covariance Matrices of VAR(1) Model (VARMACOV)

lag	crosscov
0	5.3934173	3.8597124
	3.8597124	5.0342051
1	4.5422445	4.3939641
	2.1145523	3.826089
2	3.2537114	4.0435359
	0.6244183	2.4165581
3	1.8826857	3.1652876
	-0.458977	1.0996184
4	0.676579	2.0791977
	-1.100582	0.0544993
5	-0.227704	1.0297067
	-1.347948	-0.643999

In each matrix in Figure 13.31, the diagonal elements are corresponding to the autocovariance functions of each time series. The off-diagonal elements are corresponding to the cross-covariance functions of between two series.

Figure 13.32: Log-Likelihood function of VAR(1) Model (VARMALIK)

lnl
-113.4708
2.5058678
224.43567

In Figure 13.32, the first row is the value of log-likelihood function; the second row is the sum of log determinant of the innovation variance; the last row is the weighted sum of squares of residuals.

Nonstationary VAR Process

Generate the process following the error correction model with a cointegrated rank of 1:

$\displaystyle (1-B) \mb {y}_{t} = \left( \begin{array}{r} -0.4 \\ 0.1 \\ \end{array} \right) ( 1 -2 ) \mb {y}_{t-1} + {\mbox{\boldmath $\epsilon $}}_ t$

with

$\displaystyle \Sigma = \left( \begin{array}{rr} 100 & 0 \\ 0 & 100 \\ \end{array} \right) ~ ~ \textrm{and}~ ~ \mb {y}_0 = 0$

The following statements compute the roots of characteristic function and generate simulated data.

proc iml;
/* Nonstationary  model */
sig = 100*i(2);
phi = {0.6 0.8, 0.1 0.8};
call varmasim(yt,phi) sigma=sig n=100 seed=1324; 
call vtsroot(root,phi); 
print root;

Figure 13.33: Plot of Generated Nonstationary Vector Process (VARMASIM)

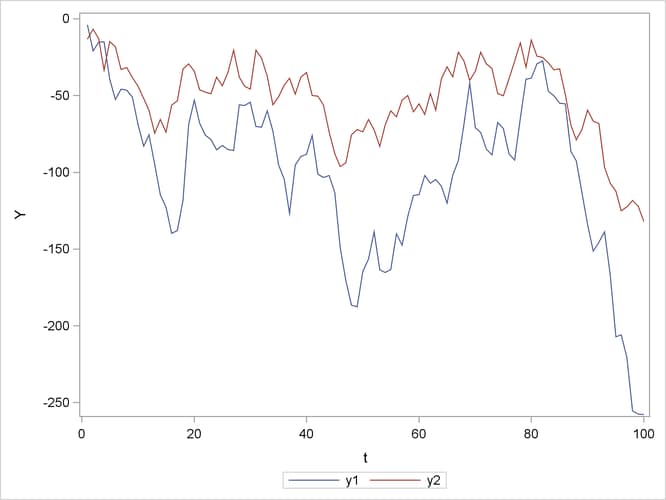
The nonstationary processes are shown in Figure 13.33 and have a comovement.

Figure 13.34: Roots of Nonstationary VAR(1) Model (VTSROOT)

root
1	0	1	0	0
0.4	0	0.4	0	0

In Figure 13.34, the first column is the real part () of the root of the characteristic function and the second one is the imaginary part (). The third column is the modulus, the squared root of . The fourth column is $Tan^{-1}(I/R)$ and the last one is the degree. Since the moduli are greater than equal to one from the third column, the series is obviously nonstationary.