Language Reference

ARMALIK Call

CALL ARMALIK (lnl, resid, std, x, phi, theta);

The ARMALIK subroutine computes the log likelihood and residuals for an autoregressive moving average (ARMA) model. The input arguments to the ARMALIK subroutine are as follows:

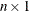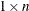x: is an $n \times 1$ or $1 \times n$ matrix that contains values of the time series (assuming mean zero).
phi: is a 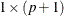$1 \times (p+1)$ matrix that contains the autoregressive parameter values. The first element is assumed to have the value 1.
theta: is a 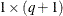$1 \times (q+1)$ matrix that contains the moving average parameter values. The first element is assumed to have the value 1.

The ARMALIK subroutine returns the following values:

lnl: specifies a 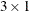$3 \times 1$ matrix that contains the log likelihood concentrated with respect to the innovation variance; the estimate of the innovation variance (the unconditional sum of squares divided by n); and the log of the determinant of the variance matrix, which is standardized to unit variance for the innovations.
resid: specifies an 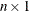$n \times 1$ matrix that contains the standardized residuals. These values are uncorrelated with a constant variance if the specified ARMA model is the correct one.
std: specifies an 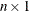$n \times 1$ matrix that contains the scale factors used to standardize the residuals. The actual residuals from the one-step-ahead predictions that use the past values can be computed as std # resid.

The ARMALIK subroutine computes the concentrated log-likelihood function for an ARMA model. The unconditional sum of squares is readily available, as are the one-step-ahead prediction residuals. Factors that can be used to generate confidence limits associated with prediction from a finite past sample are also returned.

The notational conventions for the ARMALIK subroutine are the same as those used by the ARMACOV subroutine. See the description of the ARMACOV call for the model employed. In addition, the condition $\sum _{i=0}^ q \theta _{iz}^ i \ne 0$ for $|z|<1$ should be satisfied to guard against floating-point overflow.

If the column vector $\mb{x}$ contains n values of a time series and the variance matrix is denoted $\Sigma = \sigma ^2 \mb{V}$ , where $\sigma ^2$ is the variance of the innovations, then, up to additive constants, the log likelihood, concentrated with respect to $\sigma ^2$ , is

$-\frac{n}{2} \log \left( \mb{x}^{\prime } \mb{V}^{-1} \mb{x} \right) - \frac{1}{2} \log |\mb{V}|$

The matrix $\mb{V}$ is a function of the specified ARMA model parameters. If $\mb{L}$ is the lower Cholesky root of $\mb{V}$ (that is, $\mb{V} =\mb{L}\mb{L}^{\prime })$ , then the standardized residuals are computed as resid $=\mb{L}^{-1}\mb{x}$ . The elements of std are the diagonal elements of $\mb{L}$ . The variance estimate is $\mb{x}^{\prime }\mb{V}^{-1}\mb{x}/n$ , and the log determinant is $\log |\mb{V}|$ . See Ansley (1979) for further details. Consider the following model:

$y_ t - y_ t{-1} + 0.25y_{t-2} = e_ t + 0.5e_{t-1}$

To compute the log likelihood for this model, use the following statements:

phi = {1 -1 0.25};
theta = {1 0.5};
x = {1 2 3 4 5};
call armalik(lnl, resid, std, x, phi, theta);
print lnl resid std;

Figure 24.47: Results from an ARMALIK Call

lnl	resid	std
-0.822608	0.4057513	2.4645637
0.8721154	0.9198158	1.2330147
2.3293833	0.8417343	1.0419028
	1.0854175	1.0098042
	1.2096421	1.0024125