Language Reference

BSPLINE Function

BSPLINE (x, d, k <, i> );

The BSPLINE function computes a B-spline basis. The arguments to the BSPLINE function are as follows:

x

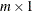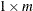is an $m \times 1$ or $1 \times m$ numeric vector.

d

is a nonnegative numeric scalar value that specifies the degree of the B-spline. The order of a B-spline is one greater than the degree.

k

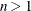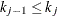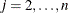is a numeric vector of size n that contains the B-spline knots or a scalar that denotes the number of interior knots. When $n > 1$ , the elements of the knot vector must be nondecreasing, $k_{j-1} \leq k_{j}$ for $j=2,\ldots ,n$ .

i

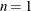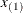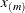is an optional argument that specifies the number of interior knots when $n=1$ and k contains a missing value. In this case the BSPLINE function constructs a vector of knots as follows: If $x_{(1)}$ and $x_{(m)}$ are the smallest and largest value in the x vector, then interior knots are placed at

$x_{(1)} + j(x_{(m)} - x_{(1)})/(k+1), \quad j=1,\ldots ,k$

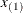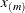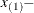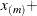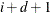In addition, d exterior knots are placed under $x_{(1)}$ and max(d,1) exterior knots are placed over $x_{(m)}$ . The exterior knots are evenly spaced and start at $x_{(1)} -$ 1E $-$ 12 and $x_{(m)} +$ 1E $-$ 12. In this case the BSPLINE function returns a matrix with m rows and $i + d + 1$ columns.

The BSPLINE function computes B-splines of degree d. Suppose that $B_{j}^ d(x)$ denotes the jth B-spline of degree d in the knot sequence $k_1,\ldots ,k_ n$ . De Boor (1978) defines the splines based on the following relationships:

$B_{j}^0(x) = \left\{ \begin{array}{ll} 1 & k_ j \leq x < k_{j+1} \cr 0 & \mbox{otherwise} \end{array} \right.$

and for $d > 0$

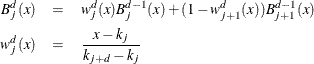
$\begin{eqnarray*} B_{j}^{d}(x) & =& w_{j}^{d}(x) B_{j}^{d-1}(x) + (1-w_{j+1}^{d}(x)) B_{j+1}^{d-1}(x) \\ w_{j}^{d}(x) & =& \frac{x-k_ j}{k_{j+d}-k_ j} \end{eqnarray*}$

Note that De Boor (1978) expresses B-splines in terms of order rather than degree; in his notation $B_{j,d} = B_ j^{d-1}$ . B-splines have many interesting properties, including the following:

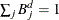
$\sum _ j B_ j^ d = 1$
The sequence 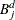$B_ j^ d$ is positive on 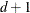$d+1$ knots and zero elsewhere.
The B-spline 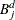$B_ j^ d$ is a piecewise polynomial of at most 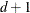$d+1$ pieces.
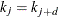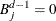If $k_ j = k_{j+d}$ , then $B_ j^{d-1} = 0$ .

See De Boor (1978) for more details. The BSPLINE function defines B-splines of degree 0 as nonzero if $k_ j < x \leq k_{j+1}$ .

A typical knot vector for calculating B-splines consists of d exterior knots smaller than the smallest data value, and $\max \{ d,1\}$ exterior knots larger than the largest data value. The remaining knots are the interior knots.

For example, the following statements creates a B-spline basis with three interior knots. The BSPLINE function returns a matrix with $3 + d + 1 = 7$ columns, shown in Figure 24.62.

x     = {2.5 3 4.5 5.1};     /* data range is [2.5, 5.1] */
knots = {0 1 2 3 4 5 6 7 8}; /* three interior knots at x=3, 4, 5 */
bsp = bspline(x, 3, knots);
print bsp[format=best7.];

Figure 24.61: B-Spline Basis

bsp
0.02083	0.47917	0.47917	0.02083	0	0	0
0	0.16667	0.66667	0.16667	0	0	0
0	0	0.02083	0.47917	0.47917	0.02083	0
0	0	0	0.1215	0.65717	0.22117	0.00017

If you pass an x vector of data values, you can also rely on the BSPLINE function to compute a knot vector for you. For example, the following statements compute B-splines of degree 2 based on four equally spaced interior knots:

n = 15;
x = ranuni(J(n, 1, 45));
bsp2 = bspline(x, 2, ., 4);
print bsp2[format=8.3];

The resulting matrix is shown in Figure 24.62.

Figure 24.62: B-Spline Basis with Four Interior Knots

bsp2
0.000	0.104	0.748	0.147	0.000	0.000	0.000
0.000	0.000	0.000	0.286	0.684	0.030	0.000
0.000	0.000	0.000	0.000	0.000	0.517	0.483
0.000	0.000	0.000	0.217	0.725	0.058	0.000
0.000	0.000	0.239	0.713	0.048	0.000	0.000
0.000	0.000	0.000	0.446	0.553	0.002	0.000
0.000	0.000	0.394	0.600	0.006	0.000	0.000
0.000	0.000	0.000	0.000	0.064	0.729	0.207
0.000	0.389	0.604	0.007	0.000	0.000	0.000
0.000	0.000	0.000	0.000	0.000	0.500	0.500
0.000	0.000	0.000	0.000	0.210	0.728	0.062
0.000	0.000	0.014	0.639	0.347	0.000	0.000
0.000	0.001	0.546	0.453	0.000	0.000	0.000
0.500	0.500	0.000	0.000	0.000	0.000	0.000
0.304	0.672	0.024	0.000	0.000	0.000	0.000