Language Reference

FROOT Function

FROOT ("fun", bounds <, opt> );

The FROOT function finds zeros of the univariate function "fun" by using Brent’s numerical root-finding method (Brent, 1973; Moler, 2004). Brent’s method uses a combination of bisection, linear interpolation, and quadratic interpolation to converge to a root when given an interval in which the function changes signs.

The arguments are as follows:

"fun"

is the name of a SAS/IML function module. The module defines the function whose roots you want to compute. The module takes one argument and returns a scalar value. You can use a GLOBAL statement to pass parameters to "fun".

bounds

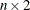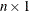is an $n\times 2$ matrix. Each row of bounds specifies an interval in which the function changes sign. This implies that there is a root inside the interval. The return value of FROOT is an $n\times 1$ vector, where the ith element contains the root in the interval bounds[i,].

opt

is an optional vector that contains three elements. Each element specifies a parameter that controls the convergence of Brent’s algorithm. A missing value specifies that the algorithm should use the default parameter value. The parameters are as follows:

opt[1]

specifies the maximum number of iterations used to search for a root. The default value is 100.

opt[2]

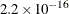specifies a tolerance that determines how close the computed root is to the true root. The default value is machine epsilon, which on many computers is approximately $2.2\times 10^{-16}$.

opt[3]

specifies a tolerance that determines how close the function at the computed root is to zero. The default value is machine epsilon.

Brent’s algorithm starts with an interval in which the function changes signs. At each step, the algorithm computes a smaller interval in which the function also changes signs. (If each interval is half the sign of the previous, this is the bisection method.) The algorithm stops when one of the following conditions is met:

  • The algorithm has performed opt[1] iterations.

  • The bounding interval $[a,b]$ is sufficiently small. If $\epsilon $ is the value of opt[2], then the algorithm stops when 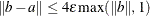$\| b-a\| \leq 4\epsilon \max (\| b\| ,1)$.

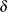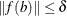  • The function that is evaluated on the interval is sufficiently small. If $\delta $ is the value of opt[3], then the algorithm stops when $\| f(b)\| \leq \delta $.

The following program defines a cubic function that has three roots. The roots are contained in the intervals $[-2,0]$, $[0,1]$, and $[1,2]$, as shown by computing the function at the endpoints of these intervals and noticing that the function changes signs on each interval. 

start Func(x);
   return( 2 - 3#x - 1#x##2 + x##3 );
finish;

bounds = {-2 0,
           0 1,
           1 2 };
fBounds = Func(bounds[,1]) || Func(bounds[,2]);
print bounds fBounds;
roots = froot( "Func", bounds);
print roots;

Figure 24.139: Bounding Intervals and Roots

bounds   fBounds  
-2 0 -4 2
0 1 2 -1
1 2 -1 0

roots
-1.618034
0.618034
2 




            

            


            
The FROOT function returns a missing value if the search fails to return a root. Usually this indicates that the function
               does not change signs at the endpoints of the specified interval. For example, the following statement returns a missing value:
               
            


r = froot("Func", {3 4});