Language Reference

LUPDT Call

CALL LUPDT (lup, bup, sup, L, z <*>, b <*>, y <*>, ssq );

The LUPDT subroutine provides updating and downdating for rank deficient linear least squares solutions, complete orthogonal factorization, and Moore-Penrose inverses.

The LUPDT subroutine returns the following values:

lup

is an 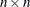$n \times n$ lower triangular matrix L that is updated or downdated by using the q rows in Z.

bup

is an 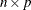$n \times p$ matrix B of right-hand sides that is updated or downdated by using the q rows in Y. If b is not specified, bup is not accessible.

sup

is a p vector of square roots of residual sum of squares that is updated or downdated by using the q rows in Y. If ssq is not specified, sup is not accessible.

The input arguments to the LUPDT subroutine are as follows:

L

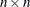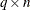specifies an $n \times n$ lower triangular matrix $\mathbf{L}$ to be updated or downdated by q row vectors z stored in the $q \times n$ matrix Z. Only the lower triangle of L is used; the upper triangle can contain any information.

z

is a 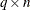$q \times n$ matrix Z used rowwise to update or downdate the matrix L.

b

specifies an optional 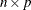$n \times p$ matrix $\mathbf{B}$ of right-hand sides that have to be updated or downdated simultaneously with L. If b is specified, the argument y must be specified.

y

specifies an optional 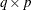$q \times p$ matrix Y used rowwise to update or downdate the right-hand-side matrix b.

ssq

specifies an optional 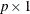$p \times 1$ vector that, if b is specified, specifies the square root of the error sum of squares that should be updated or downdated simultaneously with L and b.

The relevant formula for the LUPDT call is $\mb{\tilde{L}\tilde{L}^{\prime } = LL^{\prime } + ZZ^{\prime }}$. See the section Complete QR Decomposition with LUPDT in the documentation for the RZLIND call.