Language Reference

RZLIND Call

Subsections:

A Cholesky Root
Rank-deficient Least Squares
Moore-Penrose Inverse

CALL RZLIND (lindep, rup, bup, r <, sing> <, b> );

The RZLIND subroutine computes rank-deficient linear least squares solutions, complete orthogonal factorizations, and Moore-Penrose inverses.

The RZLIND subroutine returns the following values:

lindep: is a scalar that contains the number of linear dependencies that are recognized in 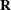$\mathbf{R}$ (number of zeroed rows in rup[n,n]).
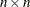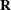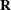rup: is the updated $n \times n$ upper triangular matrix $\mathbf{R}$ that contains zero rows corresponding to zero recognized diagonal elements in the original $\mathbf{R}$ .
bup: is the 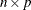$n \times p$ matrix 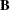$\mathbf{B}$ of right-hand sides that is updated simultaneously with 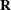$\mathbf{R}$ . If b is not specified, bup is not accessible.

The input arguments to the RZLIND subroutine are as follows:

r: specifies the 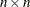$n \times n$ upper triangular matrix 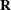$\mathbf{R}$ . Only the upper triangle of r is used; the lower triangle can contain any information.
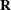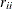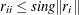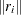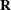sing: is an optional scalar that specifies a relative singularity criterion for the diagonal elements of $\mathbf{R}$ . The diagonal element $r_{ii}$ is considered zero if $r_{ii}\leq sing\| r_ i\|$ , where $\| r_ i\|$ is the Euclidean norm of column $r_ i$ of $\mathbf{R}$ . If the value provided for sing is not positive, the default value sing 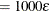$= 1000\epsilon$ is used, where $\epsilon$ is the relative machine precision.
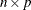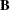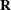b: specifies the optional $n \times p$ matrix $\mathbf{B}$ of right-hand sides that have to be updated or downdated simultaneously with $\mathbf{R}$ .

The singularity test used in the RZLIND subroutine is a relative test that uses the Euclidean norms of the columns $r_ i$ of $\mathbf{R}$ . The diagonal element $r_{ii}$ is considered as nearly zero (and the ith row is zeroed out) if the following test is true:

$r_{ii} \leq \mbox{sing} \| r_ i \| , ~ \mbox{ where } \| r_ i \| = \sqrt {r_ i^{\prime } r_ i}$

Providing an argument sing $\leq 0$ is the same as omitting the argument sing in the RZLIND call. In this case, the default is sing $= 1000 \epsilon$ , where $\epsilon$ is the relative machine precision. If $\mathbf{R}$ is computed by the QR decomposition $\mathbf{A} = \mathbf{Q}\mathbf{R}$ , then the Euclidean norm of column i of $\mathbf{R}$ is the same (except for rounding errors) as the Euclidean norm of column i of $\mathbf{A}$ .

A Cholesky Root

Consider the following application of the RZLIND subroutine. Assume that you want to compute the upper triangular Cholesky factor $\mathbf{R}$ of the $n \times n$ positive semidefinite matrix $\mathbf{A}^{\prime } \mathbf{A}$ ,

$A^{\prime } A = R^{\prime } R \mbox{ where } A \in {\mathcal R}^{m \times n}, ~ \mr{rank}(A)=r, ~ r \leq n \leq m$

The Cholesky factor $\mathbf{R}$ of a positive definite matrix $\mathbf{A}^{\prime } \mathbf{A}$ is unique (with the exception of the sign of its rows). However, the Cholesky factor of a positive semidefinite (singular) matrix $\mathbf{A}^{\prime } \mathbf{A}$ can have many different forms.

In the following example, $\mathbf{A}$ is a $12 \times 8$ matrix with linearly dependent columns $a_1 = a_2 + a_3 + a_4$ and $a_1 = a_5 + a_6 + a_7$ with $r=6$ , $n=8$ , and $m=12$ .

proc iml;
a = {1 1 0 0 1 0 0,
     1 1 0 0 1 0 0,
     1 1 0 0 0 1 0,
     1 1 0 0 0 0 1,
     1 0 1 0 1 0 0,
     1 0 1 0 0 1 0,
     1 0 1 0 0 1 0,
     1 0 1 0 0 0 1,
     1 0 0 1 1 0 0,
     1 0 0 1 0 1 0,
     1 0 0 1 0 0 1,
     1 0 0 1 0 0 1};
a = a || uniform(j(nrow(a),1,1));
aa = a` * a;
m = nrow(a); n = ncol(a);

Applying the ROOT function to the coefficient matrix $\mathbf{A}^{\prime } \mathbf{A}$ of the normal equations generates an upper triangular matrix $\mathbf{R}_1$ in which linearly dependent rows are zeroed out. The following statements verify that $\mathbf{A}^{\prime } \mathbf{A} = \mathbf{R}^{\prime }_1 \mathbf{R}_1$ :

r1 = root(aa);
ss1 = ssq(aa - r1` * r1);
print ss1 r1[format=best6.];

Figure 24.335: A Cholesky Root

ss1	r1
6.981E-29	3.4641	1.1547	1.1547	1.1547	1.1547	1.1547	1.1547	1.8012
	0	1.633	-0.816	-0.816	0.4082	-0.204	-0.204	-0.163
	0	0	1.4142	-1.414	39E-18	0.3536	-0.354	0.5325
	0	0	0	0	0	0	0	0
	0	0	0	0	1.5811	-0.791	-0.791	0.0715
	0	0	0	0	0	1.3693	-1.369	-0.194
	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0.9615

Applying the QR subroutine with column pivoting on the original matrix $\mathbf{A}$ yields a different result, but you can also verify $\mathbf{A}^{\prime } \mathbf{A} = \mathbf{R}^{\prime }_2 \mathbf{R}_2$ after pivoting the rows and columns of $\mathbf{A}^{\prime } \mathbf{A}$ :

ord = j(n,1,0);
call qr(q,r2,pivqr,lindqr,a,ord);
ss2 = ssq(aa[pivqr,pivqr] - r2` * r2);
print ss2 r2[format=best6.];

Figure 24.336: A QR Decomposition

ss2	r2
3.067E-29	-3.464	-1.155	-1.155	-1.155	-1.155	-1.801	-1.155	-1.155
	0	-1.633	0.2041	-0.408	0.8165	-0.029	0.8165	0.2041
	0	0	1.6202	-0.772	0.3086	-0.379	-0.309	-0.849
	0	0	0	-1.38	-0.173	0.4128	0.1725	1.3801
	0	0	0	0	-1.369	-0.194	1.3693	18E-17
	0	0	0	0	0	-0.961	-5E-17	52E-18
	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0

Using the RUPDT subroutine for stepwise updating of $\mathbf{R}$ by the m rows of $\mathbf{A}$ results in an upper triangular matrix $\mathbf{R}_3$ with $n-r$ nearly zero diagonal elements. However, other elements in rows with nearly zero diagonal elements can have significant values. The following statements verify that $\mathbf{A}^{\prime } \mathbf{A} = \mathbf{R}^{\prime }_3 \mathbf{R}_3$ :

r3 = shape(0,n,n);
call rupdt(rup,bup,sup,r3,a);
r3 = rup;
ss3 = ssq(aa - r3` * r3);
print ss3 r3[format=best6.];

Figure 24.337: An Updated Matrix

ss3	r3
4.4E-29	3.4641	1.1547	1.1547	1.1547	1.1547	1.1547	1.1547	1.8012
	0	-1.633	0.8165	0.8165	-0.408	0.2041	0.2041	0.1626
	0	0	-1.414	1.4142	-6E-17	-0.354	0.3536	-0.532
	0	0	0	5E-16	0.3739	0.3484	-0.722	0.0906
	0	0	0	0	-1.536	0.8984	0.6379	-0.052
	0	0	0	0	0	1.2536	-1.254	-0.246
	0	0	0	0	0	0	-4E-16	-0.168
	0	0	0	0	0	0	0	0.9316

The result $\mathbf{R}_3$ of the RUPDT subroutine can be transformed into the result $\mathbf{R}_1$ of the ROOT function by left applications of Givens rotations to zero out the remaining significant elements of rows with small diagonal elements. Applying the RZLIND subroutine to the upper triangular result $\mathbf{R}_3$ of the RUPDT subroutine generates a Cholesky factor $\mathbf{R}_4$ with rows of zeros that correspond to diagonal elements that are small. This gives the same result as the ROOT function (except for the sign of rows) if its singularity criterion recognizes the same linear dependencies.

call rzlind(lind,r4,bup,r3);
ss4 = ssq(aa - r4` * r4);
print ss4 r4[format=best6.];

Figure 24.338: The Transformed Root Matrix

ss4	r4
4.61E-29	3.4641	1.1547	1.1547	1.1547	1.1547	1.1547	1.1547	1.8012
	0	-1.633	0.8165	0.8165	-0.408	0.2041	0.2041	0.1626
	0	0	-1.414	1.4142	-6E-17	-0.354	0.3536	-0.532
	0	0	0	0	0	0	0	0
	0	0	0	0	-1.581	0.7906	0.7906	-0.071
	0	0	0	0	0	1.3693	-1.369	-0.194
	0	0	0	0	0	0	0	0
	0	0	0	0	0	0	0	0.9615

Rank-deficient Least Squares

Consider the rank-deficient linear least squares problem:

$\min _{x} \| A x - b \| ^2 \mbox{ where } \bA \in {\mathcal R}^{m \times n}, ~ \mr{rank}(\bA )=r, ~ r \leq n \leq m$

For $r=n$ , the optimal solution, $\hat{x}$ , is unique; however, for $r<n$ , the rank-deficient linear least squares problem has many optimal solutions, each of which has the same least squares residual sum of squares:

$\mbox{ss} = (\bA \hat{x} - b)^{\prime }(\bA \hat{x} - b)$

The solution of the full-rank problem, $r=n$ , is illustrated in the section The Full-Rank Linear Least Squares Problem. The following example demonstrates how to compute several solutions to the singular problem. The example uses the $12 \times 8$ matrix from the preceding section and generates a new column vector b. The vector b and the matrix $\mathbf{A}$ are shown in the output.

b = uniform(j(12,1,1));
ab = a` * b;
print b a[format=best6.];

Figure 24.339: Singular Data

b	a
0.8533943	1	1	0	0	1	0	0	0.185
0.0671846	1	1	0	0	1	0	0	0.9701
0.9570239	1	1	0	0	0	1	0	0.3998
0.297194	1	1	0	0	0	0	1	0.2594
0.2726118	1	0	1	0	1	0	0	0.9216
0.6899296	1	0	1	0	0	1	0	0.9693
0.9767649	1	0	1	0	0	1	0	0.543
0.2265075	1	0	1	0	0	0	1	0.5317
0.6882366	1	0	0	1	1	0	0	0.0498
0.4127639	1	0	0	1	0	1	0	0.0666
0.5585541	1	0	0	1	0	0	1	0.8193
0.2872256	1	0	0	1	0	0	1	0.5239

The rank-deficient linear least squares problem can be solved in the following ways. Although each method minimizes the residual sum of squares, not all of the given solutions are of minimum Euclidean length.

An SVD Solution

You can solve the rank-deficient least squares problem by using the singular value decomposition of $\mathbf{A}$ , given by $\mathbf{A} = \mathbf{U}\mathbf{D}\mathbf{V}^{\prime }$ . Take the reciprocals of significant singular values and set the small values of $\mathbf{D}$ to zero.

call svd(u,d,v,a);
t = 1e-12 * d[1];
do i=1 to n;
   if d[i] < t then d[i] = 0.;
   else d[i] = 1. / d[i];
end;
x1 = v * diag(d) * u` * b;
len1 = x1` * x1;
ss1 = ssq(a * x1 - b);
x1 = x1`;
print ss1 len1, x1[format=best6.];

Figure 24.340: SVD Solution

ss1	len1
0.5902613	0.4253851

x1
0.4001	0.1484	0.1561	0.0956	0.0792	0.3559	-0.035	-0.275

The solution $\hat{x}_1$ obtained by singular value decomposition, $\hat{x}_1 = \mathbf{V}\mathbf{D}^- \mathbf{U}^{\prime } b /4$ , is of minimum Euclidean length.

QR with Column Pivoting

You can solve the rank-deficient least squares problem by using the QR decomposition with column pivoting:

$\bA \bPi = \bQ \bR = \left[ \begin{array}{cc} \bY & \bZ \end{array} \right] \left[ \begin{array}{cc} \bR _1 & \bR _2 \\ \mb{0} & \mb{0} \end{array} \right] = \bY \left[ \begin{array}{cc} \bR _1 & \bR _2 \end{array} \right]$

Set the right part $\mathbf{R}_2$ to zero and invert the upper triangular matrix $\mathbf{R}_1$ to obtain a generalized inverse $\mathbf{R}^-$ and an optimal solution $\hat{x}_2$ :

$\bR ^- = \left[ \begin{array}{c} \bR _1^{-1} \\ \mb{0} \end{array} \right] \hat{x}_2 = \bPi \bR ^- \bY ^{\prime } b$

ord = j(n,1,0);
call qr(qtb,r2,pivqr,lindqr,a,ord,b);
nr = n - lindqr;
r = r2[1:nr,1:nr];
x2 = shape(0,n,1);
x2[pivqr] = trisolv(1,r,qtb[1:nr]) // j(lindqr,1,0.);
len2 = x2` * x2;
ss2 = ssq(a * x2 - b);
x2 = x2`;
print ss2 len2, x2 [format=best6.];

Figure 24.341: QR Solution

ss2	len2
0.5902613	1.1406975

x2
0.9122	-0.008	0	-0.061	-0.277	0	-0.391	-0.275

Notice that the residual sum of squares is minimal, but the solution $\hat{x}_2$ is not of minimum Euclidean length.

Cholesky Root

You can solve the rank-deficient least squares problem by using the result $\mathbf{R}_1$ of the ROOT function to obtain the vector piv which indicates the zero rows in the upper triangular matrix $\mathbf{R}_1$ :

r1 = root(aa);
nr = n - lind;
piv = shape(0,n,1);
j1 = 1; j2 = nr + 1;
do i=1 to n;
   if r1[i,i] ^= 0 then do;
      piv[j1] = i; j1 = j1 + 1;
   end;
   else do;
      piv[j2] = i; j2 = j2 + 1;
   end;
end;

Now compute $\hat{x}_3$ by solving the equation $\hat{x}_3 = \mathbf{R}^{-1}\mathbf{R}^{-\prime } \mathbf{A}^{\prime } b$ .

r  = r1[piv[1:nr],piv[1:nr]];
x  = trisolv(2,r,ab[piv[1:nr]]);
x  = trisolv(1,r,x);
x3 = shape(0,n,1);
x3[piv] = x // j(lind,1,0.);
len3 = x3` * x3;
ss3  = ssq(a * x3 - b);
x3 = x3`;
print ss3 len3, x3[format=best6.];

Figure 24.342: Cholesky Root Solution

ss3	len3
0.5902613	0.4601472

x3
0.4607	0.0528	0.0605	0	0.1142	0.3909	0	-0.275

Note that the residual sum of squares is minimal, but the solution $\hat{x}_3$ is not of minimum Euclidean length.

Update of Cholesky Root

You can solve the rank-deficient least squares problem by using the result $\mathbf{R}_3$ of the RUPDT call on and the vector piv (obtained in the previous solution), which indicates the zero rows of upper triangular matrices $\mathbf{R}_1$ and $\mathbf{R}_3$ . After zeroing out the rows of $\mathbf{R}_3$ belonging to small diagonal pivots, solve the system $\hat{x}_4 = \mathbf{R}^{-1}\mathbf{Y}^{\prime } b$ .

r3 = shape(0,n,n);
qtb = shape(0,n,1);
call rupdt(rup,bup,sup,r3,a,qtb,b);
r3 = rup; qtb = bup;
call rzlind(lind,r4,bup,r3,,qtb);
qtb = bup[piv[1:nr]];
x  = trisolv(1,r4[piv[1:nr],piv[1:nr]],qtb);
x4 = shape(0,n,1);
x4[piv] = x // j(lind,1,0.);
len4 = x4` * x4;
ss4 = ssq(a * x4 - b);
x4 = x4`;
print ss4 len4, x4[format=best6.];

Figure 24.343: Cholesky Update Solution

ss4	len4
0.5902613	0.4601472

x4
0.4607	0.0528	0.0605	0	0.1142	0.3909	0	-0.275

Because the matrices $\mathbf{R}_4$ and $\mathbf{R}_1$ are the same (except for the signs of rows), the solution $\hat{x}_4$ is the same as $\hat{x}_3$ .

RZLIND Method

You can solve the rank-deficient least squares problem by using the result $\mathbf{R}_4$ of the RZLIND subroutine in the previous solution, which is the result of the first step of complete QR decomposition, and perform the second step of complete QR decomposition. The rows of matrix $\mathbf{R}_4$ can be permuted to the upper trapezoidal form

$\left[ \begin{array}{cc} \widehat{\bR } & \bT \\ \mb{0} & \mb{0} \end{array} \right]$

where $\widehat{\mathbf{R}}$ is nonsingular and upper triangular and $\mathbf{T}$ is rectangular. Next, perform the second step of complete QR decomposition with the lower triangular matrix

$\left[ \begin{array}{c} \widehat{\bR }^{\prime } \\ \bT ^{\prime } \end{array} \right] = \bar{\bY } \left[ \begin{array}{c} \bar{\bR } \\ \mb{0} \end{array} \right]$

which leads to the upper triangular matrix $\bar{\mathbf{R}}$ .

r = r4[piv[1:nr],]`;
call qr(q,r5,piv2,lin2,r);
y  = trisolv(2,r5,qtb);
x5 = q * (y // j(lind,1,0.));
len5 = x5` * x5;
ss5 = ssq(a * x5 - b);
x5 = x5`;
print ss5 len5, x5[format=best6.];

Figure 24.344: RZLIND Solution

ss5	len5
0.5902613	0.4253851

x5
0.4001	0.1484	0.1561	0.0956	0.0792	0.3559	-0.035	-0.275

The solution $\hat{x}_5$ obtained by complete QR decomposition has minimum Euclidean length.

Complete QR Decomposition

You can solve the rank-deficient least squares problem by performing both steps of complete QR decomposition. The first step performs the pivoted QR decomposition of $\mathbf{A}$ ,

$\bA \bPi = \bQ \bR = \bY \left[ \begin{array}{c} \bR \\ \mb{0} \end{array} \right] = \bY \left[ \begin{array}{c} \widehat{\bR }\bT \\ \mb{0} \end{array} \right]$

where $\widehat{\mathbf{R}}$ is nonsingular and upper triangular and $\mathbf{T}$ is rectangular. The second step performs a QR decomposition as described in the previous method. This results in

$\bA \bPi = \bY \left[ \begin{array}{cc} \bar{\bR }^{\prime } & \mb{0} \\ \mb{0} & \mb{0} \end{array} \right] \bar{\bY }^{\prime }$

where $\bar{\mathbf{R}}^{\prime }$ is lower triangular.

ord  = j(n,1,0);
call qr(qtb,r2,pivqr,lindqr,a,ord,b);
nr   = n - lindqr;
r    = r2[1:nr,]`;
call qr(q,r5,piv2,lin2,r);
y    = trisolv(2,r5,qtb[1:nr]);
x6   = shape(0,n,1);
x6[pivqr] = q * (y // j(lindqr,1,0.));
len6 = x6` * x6;
ss6  = ssq(a * x6 - b);
x6   = x6`;
print ss6 len6, x6[format=best6.];

Figure 24.345: Complete QR Solution

ss6	len6
0.5902613	0.4253851

x6
0.4001	0.1484	0.1561	0.0956	0.0792	0.3559	-0.035	-0.275

The solution $\hat{x}_6$ obtained by complete QR decomposition has minimum Euclidean length.

Complete QR Decomposition with LUPDT

You can solve the rank-deficient least squares problem by performing a complete QR decomposition with the QR and LUPDT calls :

ord  = j(n,1,0);
call qr(qtb,r2,pivqr,lindqr,a,ord,b);
nr   = n - lindqr;
r    = r2[1:nr,1:nr]`; z = r2[1:nr,nr+1:n]`;
call lupdt(lup,bup,sup,r,z);
rd   = trisolv(3,lup,r2[1:nr,]);
rd   = trisolv(4,lup,rd);
x7   = shape(0,n,1);
x7[pivqr] = rd` * qtb[1:nr,];
len7 = x7` * x7;
ss7  = ssq(a * x7 - b);
x7 = x7`;
print ss7 len7, x7[format=best6.];

Figure 24.346: Complete QR Solution with Update

ss7	len7
0.5902613	0.4253851

x7
0.4001	0.1484	0.1561	0.0956	0.0792	0.3559	-0.035	-0.275

The solution $\hat{x}_7$ obtained by complete QR decomposition has minimum Euclidean length.

Complete QR Decomposition with RUPDT

You can solve the rank-deficient least squares problem by performing a complete QR decomposition with the RUPDT , RZLIND, and LUPDT calls :

r3 = shape(0,n,n);
qtb = shape(0,n,1);
call rupdt(rup,bup,sup,r3,a,qtb,b);
r3 = rup; qtb = bup;
call rzlind(lind,r4,bup,r3,,qtb);
nr = n - lind; qtb = bup;
r = r4[piv[1:nr],piv[1:nr]]`;
z = r4[piv[1:nr],piv[nr+1:n]]`;
call lupdt(lup,bup,sup,r,z);
rd = trisolv(3,lup,r4[piv[1:nr],]);
rd = trisolv(4,lup,rd);
x8 = shape(0,n,1);
x8 = rd` * qtb[piv[1:nr],];
len8 = x8` * x8;
ss8 = ssq(a * x8 - b);
x8 = x8`;
print ss8 len8, x8[format=best6.];

Figure 24.347: Complete QR Solution with Updates

ss8	len8
0.5902613	0.4253851

x8
0.4001	0.1484	0.1561	0.0956	0.0792	0.3559	-0.035	-0.275

The solution $\hat{x}_8$ obtained by complete QR decomposition has minimum Euclidean length. The same result can be obtained with the APPCORT call or the COMPORT call .

Moore-Penrose Inverse

You can use various orthogonal methods to compute the Moore-Penrose inverse $\mathbf{A}^-$ of a rectangular matrix $\mathbf{A}$ . The following examples find the Moore-Penrose inverse of the matrix $\mathbf{A}$ shown in section A Cholesky Root.

Generalized Inverse

You can find the Moore-Penrose inverse by using the GINV function . The GINV function uses the singular decomposition $\mathbf{A} = \mathbf{U}\mathbf{D}\mathbf{V}^{\prime }$ . The result $\mathbf{A}^- = \mathbf{V}\mathbf{D}^- \mathbf{U}^{\prime }$ should be identical to the result given by the next solution.

ga = ginv(a);
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss1 = ssq(t1 - t2) + ssq(t3 - t4) +
      ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss1, ga[format=best6.];

Figure 24.348: Moore-Penrose Inverse

ss1
5.097E-29

ga
	COL1	COL2	COL3	COL4	COL5	COL6	COL7	COL8	COL9	COL10	COL11	COL12
ROW1	0.1483	-0.117	0.0366	0.1318	0.0066	-0.049	0.0952	0.1469	0.1618	0.1169	-0.089	0.0105
ROW2	0.1595	0.1339	0.2154	0.2246	-0.121	-0.06	-0.046	-0.041	-0.106	-0.044	-0.063	-0.054
ROW3	0.0593	-0.235	-0.132	0.041	0.1684	0.0403	0.2002	0.3244	0.0743	-0.042	-0.205	-0.094
ROW4	-0.07	-0.015	-0.047	-0.134	-0.041	-0.029	-0.059	-0.137	0.1934	0.2027	0.179	0.1582
ROW5	0.1923	0.0783	-0.122	-0.081	0.198	-0.092	-0.031	-0.008	0.2647	-0.021	-0.11	-0.067
ROW6	-0.044	-0.06	0.2159	-0.045	-0.119	0.1443	0.1526	-0.111	-0.044	0.2205	-0.058	-0.052
ROW7	0.0004	-0.135	-0.057	0.2586	-0.072	-0.101	-0.027	0.2663	-0.059	-0.082	0.0787	0.1298
ROW8	-0.315	0.5343	0.0431	-0.262	0.1391	0.3163	-0.145	-0.311	-0.358	-0.215	0.4462	0.1266

An SVD Solution

You can find the Moore-Penrose inverse by using the singular value decomposition. The singular decomposition $\mathbf{A} = \mathbf{U}\mathbf{D}\mathbf{V}^{\prime }$ with $\mathbf{U}^{\prime }\mathbf{U} = \mathbf{I}_ m$ , $\mathbf{D} = \mr{diag}(d_ i)$ , and $\mathbf{V}^{\prime }\mathbf{V} = \mathbf{V}\mathbf{V}^{\prime } = \mathbf{I}_ n$ , can be used to compute $\mathbf{A}^- = \mathbf{V}\mathbf{D}^\dagger \mathbf{U}^{\prime }$ , with $\mathbf{D}^\dagger = \mr{diag}(d_ i^\dagger )$ and

$d_ i^\dagger = \left\{ \begin{array}{cl} 0 & \mbox{where } d_ i \leq \epsilon \\ 1/d_ i & \mbox{otherwise} \end{array} \right.$

The result $\mathbf{A}^-$ should be the same as that given by the GINV function if the singularity criterion $\epsilon$ is selected correspondingly. Since you cannot specify the criterion $\epsilon$ for the GINV function, the singular value decomposition approach can be important for applications where the GINV function uses an unsuitable $\epsilon$ criterion. The slight discrepancy between the values of SS1 and SS2 is due to rounding that occurs in the statement that computes the matrix GA.

call svd(u,d,v,a);
do i=1 to n;
   if d[i] <= 1e-10 * d[1] then d[i] = 0.;
   else d[i] = 1. / d[i];
end;
ga = v * diag(d) * u`;
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss2 = ssq(t1 - t2) + ssq(t3 - t4) +
      ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss2;

Figure 24.349: SVD Solution

ss2
5.428E-29

Complete QR Decomposition

You can find the Moore-Penrose inverse by using the complete QR decomposition. The complete QR decomposition

$\bA = \bY \left[ \begin{array}{cc} \bar{\bR }^{\prime } & \mb{0} \\ \mb{0} & \mb{0} \end{array} \right] \bar{\bY }^{\prime } \bPi ^{\prime }$

where $\bar{\bR }^{\prime }$ is lower triangular, yields the Moore-Penrose inverse

$\bA ^- = \bPi \bar{\bY } \left[ \begin{array}{cc} \bar{\bR }^{-\prime } & \mb{0} \\ \mb{0} & \mb{0} \end{array} \right] \bY ^{\prime }$

ord = j(n,1,0);
call qr(q1,r2,pivqr,lindqr,a,ord);
nr = n - lindqr;
q1 = q1[,1:nr]; r = r2[1:nr,]`;
call qr(q2,r5,piv2,lin2,r);
tt = trisolv(4,r5`,q1`);
ga = shape(0,n,m);
ga[pivqr,] = q2 * (tt // shape(0,n-nr,m));
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss3 = ssq(t1 - t2) + ssq(t3 - t4) +
      ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss3;

Figure 24.350: Complete QR Solution

ss3
7.785E-30

Complete QR Decomposition with LUPDT

You can find the Moore-Penrose inverse by using the complete QR decomposition with QR and LUPDT :

ord = j(n,1,0);
call qr(q,r2,pivqr,lindqr,a,ord);
nr = n - lindqr;
r = r2[1:nr,1:nr]`; z = r2[1:nr,nr+1:n]`;
call lupdt(lup,bup,sup,r,z);
rd = trisolv(3,lup,r2[1:nr,]);
rd = trisolv(4,lup,rd);
ga = shape(0,n,m);
ga[pivqr,] = rd` * q[,1:nr]`;
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss4 = ssq(t1 - t2) + ssq(t3 - t4) +
      ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss4;

Figure 24.351: Complete QR Solution with Update

ss4
7.899E-30

Complete QR Decomposition with RUPDT

You can find the Moore-Penrose inverse by using the complete QR decomposition with the RUPDT call and the LUPDT call :

r3 = shape(0,n,n);
y = i(m); qtb = shape(0,n,m);
call rupdt(rup,bup,sup,r3,a,qtb,y);
r3 = rup; qtb = bup;
call rzlind(lind,r4,bup,r3,,qtb);
nr = n - lind; qtb = bup;
r = r4[piv[1:nr],piv[1:nr]]`;
z = r4[piv[1:nr],piv[nr+1:n]]`;
call lupdt(lup,bup,sup,r,z);
rd = trisolv(3,lup,r4[piv[1:nr],]);
rd = trisolv(4,lup,rd);
ga = shape(0,n,m);
ga = rd` * qtb[piv[1:nr],];
t1 = a * ga; t2 = t1`;
t3 = ga * a; t4 = t3`;
ss5 = ssq(t1 - t2) + ssq(t3 - t4) +
      ssq(t1 * a - a) + ssq(t3 * ga - ga);
print ss5;

Figure 24.352: Complete QR Solution with Updates

ss5
9.077E-30