Language Reference

MCD Call

Subsections:

Example

CALL MCD (sc, coef, dist, opt, x);

The MCD subroutine computes the minimum covariance determinant estimator. The MCD call is the robust estimation of multivariate location and scatter, defined by minimizing the determinant of the covariance matrix computed from h points. The algorithm for the MCD subroutine is based on the FAST-MCD algorithm given by Rousseeuw and Van Driessen (1999).

These robust locations and covariance matrices can be used to detect multivariate outliers and leverage points. For this purpose, the MCD subroutine provides a table of robust distances.

In the following discussion, N is the number of observations and n is the number of regressors. The input arguments to the MCD subroutine are as follows:

opt

refers to an options vector with the following components (missing values are treated as default values):

opt[1]

specifies the amount of printed output. Higher option values request additional output and include the output of lower values.

0: prints no output except error messages.
1: prints most of the output.
2: additionally prints case numbers of the observations in the best subset and some basic history of the optimization process.
3: additionally prints how many subsets result in singular linear systems.

The default is opt[1]=0.

opt[2]

specifies whether the classical, initial, and final robust covariance matrices are printed. The default is opt[2]=0. The final robust covariance matrix is always returned in coef.

opt[3]

specifies whether the classical, initial, and final robust correlation matrices are printed or returned. The default is opt[3]=0.

0: does not return or print.
1: prints the robust correlation matrix.
2: returns the final robust correlation matrix in coef.
3: prints and returns the final robust correlation matrix.

opt[4]

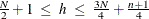specifies the quantile h used in the objective function. The default is opt[4]= $h = [\frac{N+n+1}{2}]$ . If the value of h is specified outside the range $\frac{N}{2} + 1 ~ \leq ~ h ~ \leq ~ \frac{3N}{4} + \frac{n+1}{4}$ , it is reset to the closest boundary of this region.

opt[5]

specifies the number 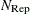$N_\mr {Rep}$ of subset generations. This option is the same as described for the LMS subroutine and the LTS subroutine . Due to computer time restrictions, not all subset combinations can be inspected for larger values of N and n.

When opt[5] is zero or missing:

If 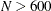$N>600$ , up to five disjoint random subsets are constructed with sizes as equal as possible, but not to exceed 300. Inside each subset, 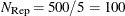$N_\mr {Rep}= 500/5 = 100$ subset combinations of n observations are chosen.

If 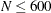$N\leq 600$ , the number of subsets is taken from the following table.

n	1	2	3	4	5	6	7 or more
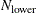
$N_\mr {lower}$	500	50	22	17	15	14	0

If the number of observations N is smaller than 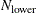$N_\mr {lower}$ , as given in the table, then all possible subsets are used; otherwise, 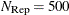$N_\mr {Rep} = 500$ subsets are chosen randomly. This means that an exhaustive search is performed for opt[5]= $-1$ .

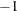x

refers to an 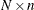$N \times n$ matrix 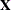$\mb{X}$ of regressors.

Missing values are not permitted in x. Missing values in opt cause default values to be used for each option.

The MCD subroutine returns the following values:

sc

is a column vector that contains the following scalar information:

sc[1]: the quantile h used in the objective function
sc[2]: number of subsets generated
sc[3]: number of subsets with singular linear systems
sc[4]: number of nonzero weights $w_ i$
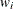
sc[5]: lowest value of the objective function 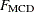$F_\mr {MCD}$ attained (smallest determinant)
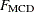
sc[6]: Mahalanobis-like distance used in the computation of the lowest value of the objective function $F_\mr {MCD}$
sc[7]: the cutoff value used for the outlier decision

coef

is a matrix with n columns that contains the following results in its rows:

coef[1,]: location of ellipsoid center
coef[2,]: eigenvalues of final robust scatter matrix
coef[3:2+n,]: the final robust scatter matrix for opt[2]=1 or opt[2]=3
coef[2+n+1:2+2n,]: the final robust correlation matrix for opt[3]=1 or opt[3]=3

dist

is a matrix with N columns that contains the following results in its rows:

dist[1,]: Mahalanobis distances
dist[2,]: robust distances based on the final estimates
dist[3,]: weights (1 for small robust distances; 0 for large robust distances)

Example

Consider the Brownlee (1965) stackloss data used in the example for the MVE subroutine.

For $N=21$ and $n=4$ (three explanatory variables including intercept), you obtain a total of 5,985 different subsets of 4 observations out of 21. If you decide not to specify opt[5], the MCD algorithm chooses 500 random sample subsets, as in the following statements:

   /* X1  X2  X3   Y  Stackloss data */
aa = { 1  80  27  89  42,
       1  80  27  88  37,
       1  75  25  90  37,
       1  62  24  87  28,
       1  62  22  87  18,
       1  62  23  87  18,
       1  62  24  93  19,
       1  62  24  93  20,
       1  58  23  87  15,
       1  58  18  80  14,
       1  58  18  89  14,
       1  58  17  88  13,
       1  58  18  82  11,
       1  58  19  93  12,
       1  50  18  89   8,
       1  50  18  86   7,
       1  50  19  72   8,
       1  50  19  79   8,
       1  50  20  80   9,
       1  56  20  82  15,
       1  70  20  91  15 };

a = aa[,2:4];
opt = j(8, 1, .);
opt[1] = 2;              /* ipri */
opt[2] = 1;              /* pcov: print COV */
opt[3] = 1;              /* pcor: print CORR */

call mcd(sc, xmcd, dist, opt, a);

A portion of the output is shown in the following figures. Figure 24.213 shows a summary of the MCD algorithm and the final h points selected.

Figure 24.213: Summary of MCD

Fast MCD by Rousseeuw and Van Driessen
Number of Variables	3
Number of Observations	21
Default Value for h	12
Specified Value for h	12
Breakdown Value	42.86
- Highest Possible Breakdown Value -

Figure 24.214 shows the observations that were chosen that are used to form the robust estimates.

Figure 24.214: Selected Observations

MCD Estimates (Obtained by Subsampling and Iteration)

The best half of the entire data set obtained after full iteration consists of the cases:

Figure 24.215 shows the MCD estimators of the location, scatter matrix, and correlation matrix. The MCD scatter matrix is multiplied by a factor to make it consistent with the data that come from a single Gaussian distribution.

Figure 24.215: MCD Estimators

MCD Location Estimate
VAR1	VAR2	VAR3
59.5	20.833333333	87.333333333

MCD Scatter Matrix Estimate
	VAR1	VAR2	VAR3
VAR1	5.1818181818	4.8181818182	4.7272727273
VAR2	4.8181818182	7.6060606061	5.0606060606
VAR3	4.7272727273	5.0606060606	19.151515152

Consistent Scatter Matrix
	VAR1	VAR2	VAR3
VAR1	8.6578437815	8.0502757968	7.8983838007
VAR2	8.0502757968	12.708297013	8.4553211199
VAR3	7.8983838007	8.4553211199	31.998580526

Figure 24.216 shows the classical Mahalanobis distances, the robust distances, and the weights that identify the outlying observations (that is, leverage points when explaining y with these three regressor variables).

Figure 24.216: Robust Distances

Classical Distances and Robust (Rousseeuw) Distances
Unsquared Mahalanobis Distance and
Unsquared Rousseeuw Distance of Each Observation
N	Mahalanobis Distances	Robust Distances	Weight
1	2.253603	12.173282	0
2	2.324745	12.255677	0
3	1.593712	9.263990	0
4	1.271898	1.401368	1.000000
5	0.303357	1.420020	1.000000
6	0.772895	1.291188	1.000000
7	1.852661	1.460370	1.000000
8	1.852661	1.460370	1.000000
9	1.360622	2.120590	1.000000
10	1.745997	1.809708	1.000000
11	1.465702	1.362278	1.000000
12	1.841504	1.667437	1.000000
13	1.482649	1.416724	1.000000
14	1.778785	1.988240	1.000000
15	1.690241	5.874858	0
16	1.291934	5.606157	0
17	2.700016	6.133319	0
18	1.503155	5.760432	0
19	1.593221	6.156248	0
20	0.807054	2.172300	1.000000
21	2.176761	7.622769	0

Robust distances are based on reweighted estimates.

The cutoff value is the square root of the 0.975 quantile of the chi square distribution with 3 degrees of freedom.

Points whose robust distance exceeds 3.0575159206 have received a zero weight in the last column above.

There were 9 such points in the data.

These may include boundary cases.

Only points whose robust distance is substantially larger than the cutoff should be considered outliers.