Language Reference

SWEEP Function

SWEEP (matrix, index-vector);

The SWEEP function sweeps matrix on the pivots indicated in index-vector to produce a new matrix.

The arguments the SWEEP function are as follows:

matrix: is a numeric matrix or literal.
index-vector: is a numeric vector that indicates the pivots.

The values of the index vector must be less than or equal to the number of rows or the number of columns in matrix, whichever is smaller.

For example, suppose that $\mb{A}$ is partitioned into

$\left[ \begin{array}{cc} \mb{R} & \mb{S} \\ \mb{T} & \mb{U} \end{array} \right]$

such that $\mb{R}$ is $q \times q$ and $\mb{U}$ is $(m-q) \times (n-q)$ . Let $I = \{ 1 2 3 \ldots q\}$ . Then, the statement B=sweep(A,I) becomes

$\left[ \begin{array}{cc} \mb{R}^{-1} & \mb{R}^{-1}\mb{S} \\ -\mb{TR}^{-1} & \mb{U}-\mb{TR}^{-1}\mb{S} \\ \end{array} \right]$

The index vector can be omitted. In this case, the function sweeps the matrix on all pivots on the main diagonal 1:MIN(nrow,ncol).

The SWEEP function has sequential and reversibility properties when the submatrix swept is positive definite:

SWEEP(SWEEP( 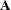$\mb{A}$ ,1),2)=SWEEP( $\mb{A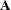}$ ,{ 1 2 })
SWEEP(SWEEP( $\mb{A}$ , $\mb{I}$ ), $\mb{I}$ )= $\mb{A}$

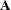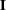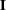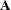
See Beaton (1964) for more information about these properties.

To use the SWEEP function for regression, suppose the matrix $\mb{A}$ contains

$\left[ \begin{array}{cc} \mb{X}^{\prime }\mb{X} & \mb{X}^{\prime } \mb{Y} \\ \mb{Y}^{\prime }\mb{X} & \mb{Y}^{\prime } \mb{Y} \end{array} \right]$

where $\mb{X}^{\prime }\mb{X}$ is $k \times k$ .

Then $\mb{B}=\mbox{SWEEP}(\mb{A},1 \ldots k)$ contains

$\left[ \begin{array}{cc} (\mb{X}^{\prime } \mb{X})^{-1} & (\mb{X}^{\prime } \mb{X})^{-1} \mb{X}^{\prime }\mb{Y} \\ -\mb{Y}^{\prime } \mb{X}(\mb{X}^{\prime } \mb{X})^{-1} & \mb{Y}^{\prime } (\mb{I}-\mb{X}(\mb{X}^{\prime } \mb{X})^{-1} \mb{X}^{\prime } ) \mb{Y} \end{array} \right]$

The partitions of $\mb{B}$ form the beta values, SSE, and a matrix proportional to the covariance of the beta values for the least squares estimates of $\mb{B}$ in the linear model

$\mb{Y} = \mb{XB} + \epsilon$

If any pivot becomes very close to zero (less than or equal to 1E $-$ 12), the row and column for that pivot are zeroed. See Goodnight (1979) for more information.

The following example uses the SWEEP function for regression:

x = { 1  1  1,
      1  2  4,
      1  3  9,
      1  4 16,
      1  5 25,
      1  6 36,
      1  7 49,
      1  8 64 };

y = {  3.929,
       5.308,
       7.239,
       9.638,
      12.866,
      17.069,
      23.191,
      31.443 };

n = nrow(x);         /* number of observations */
k = ncol(x);         /* number of variables */
xy = x||y;           /* augment design matrix */
A = xy` * xy;        /* form cross products */
S = sweep( A, 1:k );

beta = S[1:k,4];     /* parameter estimates */
sse = S[4,4];        /* sum of squared errors */
mse = sse / (n-k);   /* mean squared error */
cov = S[1:k, 1:k] # mse; /* covariance of estimates */
print cov, beta, sse;

Figure 24.406: Results of a Linear Regression

cov
0.9323716	-0.436247	0.0427693
-0.436247	0.2423596	-0.025662
0.0427693	-0.025662	0.0028513

beta
5.0693393
-1.109935
0.5396369

sse
2.395083

The SWEEP function performs most of its computations in the memory allocated for the result matrix.