The NLP Procedure
- Overview
-
Getting Started

-
Syntax
 Functional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements
Functional SummaryDictionary of OptionsPROC NLP StatementARRAY StatementBOUNDS StatementBY StatementCRPJAC StatementDECVAR StatementGRADIENT StatementHESSIAN StatementINCLUDE StatementJACNLC StatementJACOBIAN StatementLABEL StatementLINCON StatementMATRIX StatementMIN, MAX, and LSQ StatementsMINQUAD and MAXQUAD StatementsNLINCON StatementPROFILE StatementProgram Statements -
Details
 Criteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL
Criteria for OptimalityOptimization AlgorithmsFinite-Difference Approximations of DerivativesHessian and CRP Jacobian ScalingTesting the Gradient SpecificationTermination CriteriaActive Set MethodsFeasible Starting PointLine-Search MethodsRestricting the Step LengthComputational ProblemsCovariance MatrixInput and Output Data SetsDisplayed OutputMissing ValuesComputational ResourcesMemory LimitRewriting NLP Models for PROC OPTMODEL -
Examples

- References
Almost all line-search algorithms use iterative extrapolation techniques which can easily lead them to (feasible) points where
the objective function ![]() is no longer defined. (e.g., resulting in indefinite matrices for ML estimation) or difficult to compute (e.g., resulting
in floating point overflows). Therefore, PROC NLP provides options restricting the step length
is no longer defined. (e.g., resulting in indefinite matrices for ML estimation) or difficult to compute (e.g., resulting
in floating point overflows). Therefore, PROC NLP provides options restricting the step length ![]() or trust region radius
or trust region radius ![]() , especially during the first main iterations.
, especially during the first main iterations.
The inner product ![]() of the gradient
of the gradient ![]() and the search direction
and the search direction ![]() is the slope of
is the slope of ![]() along the search direction
along the search direction ![]() . The default starting value
. The default starting value ![]() in each line-search algorithm
in each line-search algorithm ![]() during the main iteration
during the main iteration ![]() is computed in three steps:
is computed in three steps:
-
The first step uses either the difference
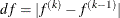 of the function values during the last two consecutive iterations or the final step length value
of the function values during the last two consecutive iterations or the final step length value 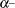 of the last iteration
of the last iteration 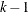 to compute a first value of
to compute a first value of 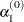 .
.
-
Not using the DAMPSTEP=
 option:
option:
![\[ \alpha _1^{(0)} = \left\{ \begin{array}{ll} \emph{step}, & \mbox{ if } 0.1 \le \mi {step} \le 10 \\[0.1in] 10, & \mbox{ if }\mi {step} > 10 \\[0.1in] 0.1, & \mbox{ if }\mi {step} < 0.1 \end{array} \right. \]](images/ormplpug_nlp0384.png)
with
![\[ \emph{step} = \left\{ \begin{array}{ll} df / |g^ Ts|, & \mbox{if } |g^ Ts| \ge \epsilon \max (100\mi {df},1) \\[0.1in] 1, & \mbox{otherwise} \end{array} \right. \]](images/ormplpug_nlp0385.png)
This value of
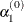 can be too large and lead to a difficult or impossible function evaluation, especially for highly nonlinear functions such
as the EXP function.
can be too large and lead to a difficult or impossible function evaluation, especially for highly nonlinear functions such
as the EXP function.
-
Using the DAMPSTEP=
 option:
option:
![\[ \alpha _1^{(0)} = \min (1,r \alpha ^\_ ) \]](images/ormplpug_nlp0387.png)
The initial value for the new step length can be no larger than
 times the final step length
times the final step length 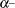 of the previous iteration. The default value is
of the previous iteration. The default value is 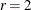 .
.
-
-
During the first five iterations, the second step enables you to reduce
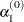 to a smaller starting value
to a smaller starting value 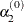 using the INSTEP=
using the INSTEP= option:
option:
![\[ \alpha _2^{(0)} = \min (\alpha _1^{(0)},r) \]](images/ormplpug_nlp0389.png)
After more than five iterations,
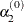 is set to
is set to 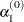 .
.
-
The third step can further reduce the step length by
![\[ \alpha _3^{(0)} = \min (\alpha _2^{(0)},\min (10,u)) \]](images/ormplpug_nlp0390.png)
where
 is the maximum length of a step inside the feasible region.
is the maximum length of a step inside the feasible region.
The INSTEP=![]() option lets you specify
a smaller or larger radius
option lets you specify
a smaller or larger radius ![]() of the trust region used in the first iteration of the trust region, double dogleg, and Levenberg-Marquardt algorithms. The
default initial trust region radius
of the trust region used in the first iteration of the trust region, double dogleg, and Levenberg-Marquardt algorithms. The
default initial trust region radius ![]() is the length of the scaled gradient (Moré 1978). This step corresponds to the default radius factor of
is the length of the scaled gradient (Moré 1978). This step corresponds to the default radius factor of ![]() . In most practical applications of the TRUREG, DBLDOG, and LEVMAR algorithms, this choice is
successful. However, for bad initial values and highly nonlinear objective functions (such as the EXP function), the default
start radius can result in arithmetic overflows. If this happens, you may try decreasing values of INSTEP=
. In most practical applications of the TRUREG, DBLDOG, and LEVMAR algorithms, this choice is
successful. However, for bad initial values and highly nonlinear objective functions (such as the EXP function), the default
start radius can result in arithmetic overflows. If this happens, you may try decreasing values of INSTEP=![]() ,
, ![]() , until the iteration starts successfully. A small factor
, until the iteration starts successfully. A small factor ![]() also affects the trust region radius
also affects the trust region radius ![]() of the next steps because the radius is changed in each iteration by a factor
of the next steps because the radius is changed in each iteration by a factor ![]() , depending on the ratio
, depending on the ratio ![]() expressing the goodness of quadratic function approximation. Reducing the radius
expressing the goodness of quadratic function approximation. Reducing the radius ![]() corresponds to increasing the ridge parameter
corresponds to increasing the ridge parameter ![]() , producing smaller steps directed more closely toward the (negative) gradient direction.
, producing smaller steps directed more closely toward the (negative) gradient direction.