The Linear Programming Solver
- Overview
- Getting Started
-
Syntax

-
Details
 PresolvePricing Strategies for the Primal and Dual Simplex AlgorithmsThe Network Simplex AlgorithmThe Interior Point AlgorithmIteration Log for the Primal and Dual Simplex AlgorithmsIteration Log for the Network Simplex AlgorithmIteration Log for the Interior Point AlgorithmIteration Log for the Crossover AlgorithmConcurrent LPParallel ProcessingProblem StatisticsVariable and Constraint StatusIrreducible Infeasible SetMacro Variable _OROPTMODEL_
PresolvePricing Strategies for the Primal and Dual Simplex AlgorithmsThe Network Simplex AlgorithmThe Interior Point AlgorithmIteration Log for the Primal and Dual Simplex AlgorithmsIteration Log for the Network Simplex AlgorithmIteration Log for the Interior Point AlgorithmIteration Log for the Crossover AlgorithmConcurrent LPParallel ProcessingProblem StatisticsVariable and Constraint StatusIrreducible Infeasible SetMacro Variable _OROPTMODEL_ -
Examples
 Diet ProblemReoptimizing the Diet Problem Using BASIS=WARMSTARTTwo-Person Zero-Sum GameFinding an Irreducible Infeasible SetUsing the Network Simplex AlgorithmMigration to OPTMODEL: Generalized NetworksMigration to OPTMODEL: Maximum FlowMigration to OPTMODEL: Production, Inventory, DistributionMigration to OPTMODEL: Shortest Path
Diet ProblemReoptimizing the Diet Problem Using BASIS=WARMSTARTTwo-Person Zero-Sum GameFinding an Irreducible Infeasible SetUsing the Network Simplex AlgorithmMigration to OPTMODEL: Generalized NetworksMigration to OPTMODEL: Maximum FlowMigration to OPTMODEL: Production, Inventory, DistributionMigration to OPTMODEL: Shortest Path - References
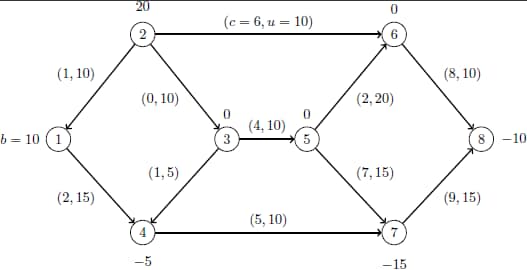
This example demonstrates how you can use the network simplex algorithm to find the minimum-cost flow in a directed graph. Consider the directed graph in Figure 7.4, which appears in Ahuja, Magnanti, and Orlin (1993).
You can use the following SAS statements to create the input data sets nodedata and arcdata:
data nodedata; input _node_ $ _sd_; datalines; 1 10 2 20 3 0 4 -5 5 0 6 0 7 -15 8 -10 ; data arcdata; input _tail_ $ _head_ $ _lo_ _capac_ _cost_; datalines; 1 4 0 15 2 2 1 0 10 1 2 3 0 10 0 2 6 0 10 6 3 4 0 5 1 3 5 0 10 4 4 7 0 10 5 5 6 0 20 2 5 7 0 15 7 6 8 0 10 8 7 8 0 15 9 ;
You can use the following call to PROC OPTMODEL to find the minimum-cost flow:
proc optmodel;
set <str> NODES;
num supply_demand {NODES};
set <str,str> ARCS;
num arcLower {ARCS};
num arcUpper {ARCS};
num arcCost {ARCS};
read data arcdata into ARCS=[_tail_ _head_]
arcLower=_lo_ arcUpper=_capac_ arcCost=_cost_;
read data nodedata into NODES=[_node_] supply_demand=_sd_;
var flow {<i,j> in ARCS} >= arcLower[i,j] <= arcUpper[i,j];
min obj = sum {<i,j> in ARCS} arcCost[i,j] * flow[i,j];
con balance {i in NODES}:
sum {<(i),j> in ARCS} flow[i,j] - sum {<j,(i)> in ARCS} flow[j,i]
= supply_demand[i];
solve with lp / algorithm=ns scale=none logfreq=1;
print flow;
quit;
%put &_OROPTMODEL_;
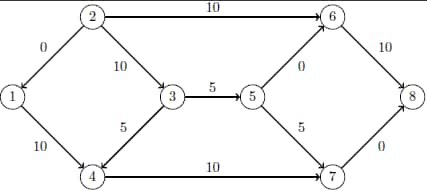
The optimal solution is displayed in Output 7.5.1.
Output 7.5.1: Network Simplex Algorithm: Primal Solution Output
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | obj |
| Objective Type | Linear |
| Number of Variables | 11 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 11 |
| Free | 0 |
| Fixed | 0 |
| Number of Constraints | 8 |
| Linear LE (<=) | 0 |
| Linear EQ (=) | 8 |
| Linear GE (>=) | 0 |
| Linear Range | 0 |
| Constraint Coefficients | 22 |
The optimal solution is represented graphically in Figure 7.5.
The iteration log is displayed in Output 7.5.2.
Output 7.5.2: Log: Solution Progress
| NOTE: There were 11 observations read from the data set WORK.ARCDATA. |
| NOTE: There were 8 observations read from the data set WORK.NODEDATA. |
| NOTE: Problem generation will use 4 threads. |
| NOTE: The problem has 11 variables (0 free, 0 fixed). |
| NOTE: The problem has 8 linear constraints (0 LE, 8 EQ, 0 GE, 0 range). |
| NOTE: The problem has 22 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The problem is a pure network instance; PRESOLVER=NONE is used. |
| NOTE: The LP presolver value NONE is applied. |
| NOTE: The LP solver is called. |
| NOTE: The Network Simplex algorithm is used. |
| NOTE: The network has 8 rows (100.00%), 11 columns (100.00%), and 1 component. |
| NOTE: The network extraction and setup time is 0.00 seconds. |
| Primal Primal Dual |
| Iteration Objective Infeasibility Infeasibility Time |
| 1 0.000000E+00 2.000000E+01 8.900000E+01 0.00 |
| 2 0.000000E+00 2.000000E+01 8.900000E+01 0.00 |
| 3 5.000000E+00 1.500000E+01 8.400000E+01 0.00 |
| 4 5.000000E+00 1.500000E+01 8.300000E+01 0.00 |
| 5 7.500000E+01 1.500000E+01 8.300000E+01 0.00 |
| 6 7.500000E+01 1.500000E+01 7.900000E+01 0.00 |
| 7 1.300000E+02 1.000000E+01 7.600000E+01 0.00 |
| 8 2.700000E+02 0.000000E+00 0.000000E+00 0.00 |
| NOTE: The Network Simplex solve time is 0.00 seconds. |
| NOTE: The total Network Simplex solve time is 0.00 seconds. |
| NOTE: Optimal. |
| NOTE: Objective = 270. |
| NOTE: The PROCEDURE OPTMODEL printed pages 1-2. |
| STATUS=OK ALGORITHM=NS SOLUTION_STATUS=OPTIMAL OBJECTIVE=270 |
| PRIMAL_INFEASIBILITY=0 DUAL_INFEASIBILITY=0 BOUND_INFEASIBILITY=0 ITERATIONS=8 |
| ITERATIONS2=0 PRESOLVE_TIME=0.00 SOLUTION_TIME=0.00 |
Now, suppose there is a budget on the flow that comes out of arc 2: the total arc cost of flow that comes out of arc 2 cannot exceed 50. You can use the following call to PROC OPTMODEL to find the minimum-cost flow:
proc optmodel;
set <str> NODES;
num supply_demand {NODES};
set <str,str> ARCS;
num arcLower {ARCS};
num arcUpper {ARCS};
num arcCost {ARCS};
read data arcdata into ARCS=[_tail_ _head_]
arcLower=_lo_ arcUpper=_capac_ arcCost=_cost_;
read data nodedata into NODES=[_node_] supply_demand=_sd_;
var flow {<i,j> in ARCS} >= arcLower[i,j] <= arcUpper[i,j];
min obj = sum {<i,j> in ARCS} arcCost[i,j] * flow[i,j];
con balance {i in NODES}:
sum {<(i),j> in ARCS} flow[i,j] - sum {<j,(i)> in ARCS} flow[j,i]
= supply_demand[i];
con budgetOn2:
sum {<i,j> in ARCS: i='2'} arcCost[i,j] * flow[i,j] <= 50;
solve with lp / algorithm=ns scale=none logfreq=1;
print flow;
quit;
%put &_OROPTMODEL_;
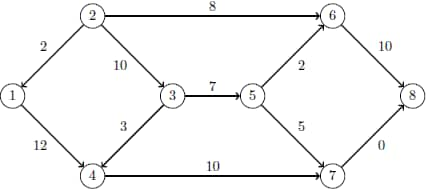
The optimal solution is displayed in Output 7.5.3.
Output 7.5.3: Network Simplex Algorithm: Primal Solution Output
| Problem Summary | |
|---|---|
| Objective Sense | Minimization |
| Objective Function | obj |
| Objective Type | Linear |
| Number of Variables | 11 |
| Bounded Above | 0 |
| Bounded Below | 0 |
| Bounded Below and Above | 11 |
| Free | 0 |
| Fixed | 0 |
| Number of Constraints | 9 |
| Linear LE (<=) | 1 |
| Linear EQ (=) | 8 |
| Linear GE (>=) | 0 |
| Linear Range | 0 |
| Constraint Coefficients | 24 |
The optimal solution is represented graphically in Figure 7.6.
The iteration log is displayed in Output 7.5.4. Note that the network simplex algorithm extracts a subnetwork in this case.
Output 7.5.4: Log: Solution Progress
| NOTE: There were 11 observations read from the data set WORK.ARCDATA. |
| NOTE: There were 8 observations read from the data set WORK.NODEDATA. |
| NOTE: Problem generation will use 4 threads. |
| NOTE: The problem has 11 variables (0 free, 0 fixed). |
| NOTE: The problem has 9 linear constraints (1 LE, 8 EQ, 0 GE, 0 range). |
| NOTE: The problem has 24 linear constraint coefficients. |
| NOTE: The problem has 0 nonlinear constraints (0 LE, 0 EQ, 0 GE, 0 range). |
| NOTE: The LP presolver value AUTOMATIC is applied. |
| NOTE: The LP presolver removed 4 variables and 4 constraints. |
| NOTE: The LP presolver removed 7 constraint coefficients. |
| NOTE: The presolved problem has 7 variables, 5 constraints, and 17 constraint |
| coefficients. |
| NOTE: The LP solver is called. |
| NOTE: The Network Simplex algorithm is used. |
| NOTE: The network has 4 rows (80.00%), 7 columns (100.00%), and 1 component. |
| NOTE: The network extraction and setup time is 0.00 seconds. |
| Primal Primal Dual |
| Iteration Objective Infeasibility Infeasibility Time |
| 1 8.015000E+01 1.006000E+01 5.500000E+01 0.02 |
| 2 1.053000E+02 5.030000E+00 5.400000E+01 0.02 |
| 3 1.053000E+02 5.030000E+00 5.400000E+01 0.02 |
| 4 1.353000E+02 3.000000E-02 4.900000E+01 0.02 |
| 5 1.356300E+02 0.000000E+00 4.700000E+01 0.02 |
| 6 1.356300E+02 0.000000E+00 0.000000E+00 0.02 |
| 7 2.700000E+02 0.000000E+00 0.000000E+00 0.02 |
| NOTE: The Network Simplex solve time is 0.00 seconds. |
| NOTE: The total Network Simplex solve time is 0.02 seconds. |
| NOTE: The Dual Simplex algorithm is used. |
| Objective Entering Leaving |
| Phase Iteration Value Time Variable Variable |
| D 2 1 2.700000E+02 0 flow['5','6'] |
| budgetOn2 (S) |
| D 2 2 2.740000E+02 0 |
| NOTE: Optimal. |
| NOTE: Objective = 274. |
| NOTE: The Simplex solve time is 0.05 seconds. |
| NOTE: The PROCEDURE OPTMODEL printed pages 4-5. |
| STATUS=OK ALGORITHM=NS SOLUTION_STATUS=OPTIMAL OBJECTIVE=274 |
| PRIMAL_INFEASIBILITY=0 DUAL_INFEASIBILITY=0 BOUND_INFEASIBILITY=0 ITERATIONS=7 |
| ITERATIONS2=2 PRESOLVE_TIME=0.00 SOLUTION_TIME=0.05 |