The OPTMODEL Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Named ParametersIndexingTypesNamesParametersExpressionsIdentifier ExpressionsFunction ExpressionsIndex SetsOPTMODEL Expression ExtensionsConditions of OptimalityData Set Input/OutputControl FlowFormatted OutputODS Table and Variable NamesConstraintsSuffixesInteger Variable SuffixesDual ValuesReduced CostsPresolverModel UpdateMultiple SubproblemsMultiple SolutionsProblem SymbolsOPTMODEL OptionsAutomatic DifferentiationConversionsFCMP RoutinesMore on Index SetsThreaded ProcessingMacro Variable _OROPTMODEL_Rewriting PROC NLP Models for PROC OPTMODEL
Named ParametersIndexingTypesNamesParametersExpressionsIdentifier ExpressionsFunction ExpressionsIndex SetsOPTMODEL Expression ExtensionsConditions of OptimalityData Set Input/OutputControl FlowFormatted OutputODS Table and Variable NamesConstraintsSuffixesInteger Variable SuffixesDual ValuesReduced CostsPresolverModel UpdateMultiple SubproblemsMultiple SolutionsProblem SymbolsOPTMODEL OptionsAutomatic DifferentiationConversionsFCMP RoutinesMore on Index SetsThreaded ProcessingMacro Variable _OROPTMODEL_Rewriting PROC NLP Models for PROC OPTMODEL -
Examples

- References
A standard linear program has the following formulation:
where
|
|
|
|
is the vector of decision variables |
|
|
|
|
is the matrix of constraints |
|
|
|
|
is the vector of objective function coefficients |
|
|
|
|
is the vector of constraints right-hand sides (RHS) |
This formulation is called the primal problem. The corresponding dual problem (see the section Dual Values) is
![\[ \begin{array}{rl} \displaystyle \mathop {\textrm{maximize}}& \mathbf{b}^{T} \mathbf{y} \\ \textrm{subject to}& \mathbf{A}^{T} \mathbf{y} \le \mathbf{c} \\ & \mathbf{y} \ge 0 \end{array} \]](images/ormpug_optmodel0059.png)
where ![]() is the vector of dual variables.
is the vector of dual variables.
The vectors ![]() and
and ![]() are optimal to the primal and dual problems, respectively, only if there exist primal slack variables
are optimal to the primal and dual problems, respectively, only if there exist primal slack variables ![]() and dual slack variables
and dual slack variables ![]() such that the following Karush-Kuhn-Tucker (KKT) conditions are satisfied:
such that the following Karush-Kuhn-Tucker (KKT) conditions are satisfied:
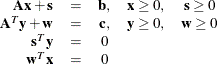
The first line of equations defines primal feasibility, the second line of equations defines dual feasibility, and the last two equations are called the complementary slackness conditions.
To facilitate discussion of optimality conditions in nonlinear programming, you write the general form of nonlinear optimization
problems by grouping the equality constraints and inequality constraints. You also write all the general nonlinear inequality
constraints and bound constraints in one form as "![]() " inequality constraints. Thus, you have the following formulation:
" inequality constraints. Thus, you have the following formulation:
![\[ \begin{array}{lll} \displaystyle \mathop {\textrm{minimize}}_{x\in {\mathbb R}^ n} & f(x) \\ \textrm{subject to}& c_ i(x) = 0, & i \in {\mathcal E} \\ & c_ i(x) \ge 0, & i \in {\mathcal I} \end{array} \]](images/ormpug_optmodel0066.png)
where ![]() is the set of indices of the equality constraints,
is the set of indices of the equality constraints, ![]() is the set of indices of the inequality constraints, and
is the set of indices of the inequality constraints, and ![]() .
.
A point x is feasible if it satisfies all the constraints ![]() and
and ![]() . The feasible region
. The feasible region ![]() consists of all the feasible points. In unconstrained cases, the feasible region
consists of all the feasible points. In unconstrained cases, the feasible region ![]() is the entire
is the entire ![]() space.
space.
A feasible point ![]() is a local solution of the problem if there exists a neighborhood
is a local solution of the problem if there exists a neighborhood ![]() of
of ![]() such that
such that
Further, a feasible point ![]() is a strict local solution if strict inequality holds in the preceding case; that is,
is a strict local solution if strict inequality holds in the preceding case; that is,
A feasible point ![]() is a global solution of the problem if no point in
is a global solution of the problem if no point in ![]() has a smaller function value than
has a smaller function value than ![]() ); that is,
); that is,
The following conditions hold true for unconstrained optimization problems:
-
First-order necessary conditions: If
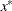 is a local solution and
is a local solution and 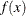 is continuously differentiable in some neighborhood of
is continuously differentiable in some neighborhood of 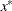 , then
, then
![\[ \nabla \! f(x^*) = 0 \]](images/ormpug_optmodel0079.png)
-
Second-order necessary conditions: If
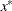 is a local solution and
is a local solution and 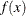 is twice continuously differentiable in some neighborhood of
is twice continuously differentiable in some neighborhood of 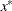 , then
, then 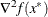 is positive semidefinite.
is positive semidefinite.
-
Second-order sufficient conditions: If
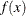 is twice continuously differentiable in some neighborhood of
is twice continuously differentiable in some neighborhood of 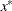 ,
, 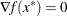 , and
, and 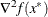 is positive definite, then
is positive definite, then 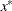 is a strict local solution.
is a strict local solution.
For constrained optimization problems, the Lagrangian function is defined as follows:
where ![]() , are called Lagrange multipliers.
, are called Lagrange multipliers. ![]() is used to denote the gradient of the Lagrangian function with respect to x, and
is used to denote the gradient of the Lagrangian function with respect to x, and ![]() is used to denote the Hessian of the Lagrangian function with respect to x. The active set at a feasible point x is defined as
is used to denote the Hessian of the Lagrangian function with respect to x. The active set at a feasible point x is defined as
You also need the following definition before you can state the first-order and second-order necessary conditions:
-
Linear independence constraint qualification and regular point: A point x is said to satisfy the linear independence constraint qualification if the gradients of active constraints
![\[ \nabla \! c_ i(x),\quad i\in {\mathcal A}(x) \]](images/ormpug_optmodel0087.png)
are linearly independent. Such a point x is called a regular point.
You now state the theorems that are essential in the analysis and design of algorithms for constrained optimization:
-
First-order necessary conditions: Suppose that
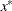 is a local minimum and also a regular point. If
is a local minimum and also a regular point. If 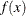 and
and 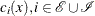 , are continuously differentiable, there exist Lagrange multipliers
, are continuously differentiable, there exist Lagrange multipliers 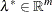 such that the following conditions hold:
such that the following conditions hold: 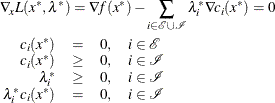
The preceding conditions are often known as the Karush-Kuhn-Tucker conditions, or KKT conditions for short.
-
Second-order necessary conditions: Suppose that
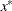 is a local minimum and also a regular point. Let
is a local minimum and also a regular point. Let 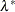 be the Lagrange multipliers that satisfy the KKT conditions. If
be the Lagrange multipliers that satisfy the KKT conditions. If 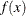 and
and 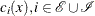 , are twice continuously differentiable, the following conditions hold:
, are twice continuously differentiable, the following conditions hold: ![\[ z^ T \nabla _{\! x}^2 L(x^*,\lambda ^*)z \ge 0 \]](images/ormpug_optmodel0093.png)
for all
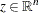 that satisfy
that satisfy
![\[ \nabla \! c_ i(x^*)^ Tz = 0,\quad i\in {\mathcal A}(x^{*}) \]](images/ormpug_optmodel0095.png)
-
Second-order sufficient conditions: Suppose there exist a point
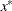 and some Lagrange multipliers
and some Lagrange multipliers 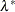 such that the KKT conditions are satisfied. If
such that the KKT conditions are satisfied. If ![\[ z^ T \nabla _{\! x}^2 L(x^*,\lambda ^*)z > 0 \]](images/ormpug_optmodel0096.png)
for all
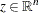 that satisfy
that satisfy
![\[ \nabla \! c_ i(x^*)^ Tz = 0,\quad i\in {\mathcal A}(x^*) \]](images/ormpug_optmodel0097.png)
then
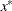 is a strict local solution.
is a strict local solution.
Note that the set of all such z’s forms the null space of the matrix
![$\left[\nabla \! c_ i(x^*)^ T \right]_{i\in {\mathcal A}(x^{*})}$](images/ormpug_optmodel0098.png) . Thus, you can search for strict local solutions by numerically checking the Hessian of the Lagrangian function projected
onto the null space. For a rigorous treatment of the optimality conditions, see Fletcher (1987) and Nocedal and Wright (1999).
. Thus, you can search for strict local solutions by numerically checking the Hessian of the Lagrangian function projected
onto the null space. For a rigorous treatment of the optimality conditions, see Fletcher (1987) and Nocedal and Wright (1999).