Evaluating Single-Sampling Plans
You can use the Base SAS functions PROBBNML and PROBHYPR to evaluate single-sampling plans. Measures of the performance of single-sampling plans include
-
the probability of acceptance
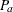
-
the average sample number ASN
-
the average outgoing quality AOQ
-
the average total inspection ATI
Probability of Acceptance
Since ![]() is the probability of finding c or fewer defectives in the sample, you can calculate the acceptance probability using the function PROBHYPR
is the probability of finding c or fewer defectives in the sample, you can calculate the acceptance probability using the function PROBHYPR![]() for Type A sampling and the function PROBBNML
for Type A sampling and the function PROBBNML![]() for Type B sampling.
for Type B sampling.
For example, the following statements calculate ![]() for the plan n = 20, c = 1 when sampling from a single lot of size N = 120 that contains D = 22 nonconforming items, resulting in a value of 0.0762970752:
for the plan n = 20, c = 1 when sampling from a single lot of size N = 120 that contains D = 22 nonconforming items, resulting in a value of 0.0762970752:
data; prob=probhypr(120,22,20,1); put prob; run;
Similarly, the following statements calculate ![]() for the plan n = 20, c = 1 when sampling from a series of lots for which the proportion of nonconforming items is p = 0.18, resulting in a value of 0.1018322793:
for the plan n = 20, c = 1 when sampling from a series of lots for which the proportion of nonconforming items is p = 0.18, resulting in a value of 0.1018322793:
data; prob=probbnml(0.18,20,1); put prob; run;
Other Measures of Performance
The measures ASN, AOQ, and ATI are meaningful only for Type B sampling and can be calculated using the PROBBNML function. For reference, the following equations are provided.
Average sample number: Following the notation of Schilling (1982), let ![]() denote the probability of finding c or fewer nonconforming items in a sample of size n. Note that
denote the probability of finding c or fewer nonconforming items in a sample of size n. Note that ![]() is equivalent to PROBBNML
is equivalent to PROBBNML![]() . Then, depending on the mode of inspection, the average sample number can be expressed as shown in the following table:
. Then, depending on the mode of inspection, the average sample number can be expressed as shown in the following table:
|
Mode of Inspection |
ASN |
|---|---|
|
Full |
n |
|
Semicurtailed |
|
|
Fully curtailed |
|
Average outgoing quality can be expressed as
|
|
if the nonconforming items found are replaced with conforming items, and as
|
|
if the nonconforming items found are not replaced.
Average total inspection can be expressed as
|
|