The following entries provide detailed descriptions of the options specific to the PPPLOT statement. See Dictionary of Common Options: CAPABILITY Procedure for detailed descriptions of options common to all the plot statements.
- ALPHA=value
-
specifies the shape parameter

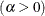 for P-P plots requested with the BETA, GAMMA, PARETO, and POWER options. For examples, see the entries for the distribution options.
for P-P plots requested with the BETA, GAMMA, PARETO, and POWER options. For examples, see the entries for the distribution options.
- BETA<(beta-options)>
-
creates a beta P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
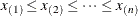
The y-coordinate of the ith point is the empirical cdf value
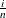 . The x-coordinate is the theoretical beta cdf value
. The x-coordinate is the theoretical beta cdf value
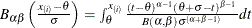 where
where 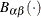 is the normalized incomplete beta function,
is the normalized incomplete beta function, 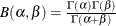 , and
, and  lower threshold parameter
lower threshold parameter  scale parameter
scale parameter 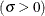
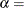 first shape parameter
first shape parameter 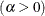
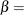 second shape parameter
second shape parameter 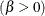
You can specify
 ,
, 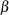 ,
,  , and
, and  with the ALPHA=, BETA=, SIGMA=, and THETA= beta-options, as illustrated in the following example:
with the ALPHA=, BETA=, SIGMA=, and THETA= beta-options, as illustrated in the following example:
proc capability data=measures; ppplot width / beta(theta=1 sigma=2 alpha=3 beta=4); run;
If you do not specify values for these parameters, then by default,
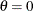 ,
, 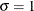 , and maximum likelihood estimates are calculated for
, and maximum likelihood estimates are calculated for  and
and 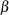 .
.
IMPORTANT: If the default unit interval (0,1) does not adequately describe the range of your data, then you should specify THETA=
 and SIGMA=
and SIGMA= so that your data fall in the interval
so that your data fall in the interval 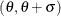 .
.
If the data are beta distributed with parameters
 ,
, 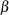 ,
,  , and
, and  , then the points on the plot for ALPHA=
, then the points on the plot for ALPHA= , BETA=
, BETA=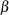 , SIGMA=
, SIGMA= , and THETA=
, and THETA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 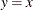 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
beta distribution is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
beta distribution is a good fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option.
- BETA=value
-
specifies the shape parameter
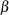
 for P-P plots requested with the BETA distribution option. See the preceding entry for the BETA distribution option for an
example.
for P-P plots requested with the BETA distribution option. See the preceding entry for the BETA distribution option for an
example.
- C=value
-
specifies the shape parameter c (c > 0) for P-P plots requested with the WEIBULL option. See the entry for the WEIBULL option for examples.
-
EXPONENTIAL<(exponential-options)>
EXP<(exponential-options)> -
creates an exponential P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
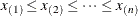
The y-coordinate of the ith point is the empirical cdf value
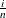 . The x-coordinate is the theoretical exponential cdf value
. The x-coordinate is the theoretical exponential cdf value
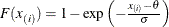 where
where 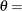 threshold parameter
threshold parameter 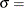 scale parameter
scale parameter 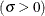
You can specify
 and
and  with the SIGMA= and THETA= exponential-options, as illustrated in the following example:
with the SIGMA= and THETA= exponential-options, as illustrated in the following example:
proc capability data=measures; ppplot width / exponential(theta=1 sigma=2); run;
If you do not specify values for these parameters, then by default,
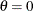 and a maximum likelihood estimate is calculated for
and a maximum likelihood estimate is calculated for  .
.
IMPORTANT: Your data must be greater than or equal to the lower threshold
 . If the default
. If the default 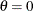 is not an adequate lower bound for your data, specify
is not an adequate lower bound for your data, specify  with the THETA= option.
with the THETA= option.
If the data are exponentially distributed with parameters
 and
and  , the points on the plot for SIGMA=
, the points on the plot for SIGMA= and THETA=
and THETA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 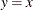 , which is displayed by default.
Agreement between the diagonal line and the point pattern is evidence that the specified exponential distribution is a good
fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option.
, which is displayed by default.
Agreement between the diagonal line and the point pattern is evidence that the specified exponential distribution is a good
fit. You can specify the SCALE= option as an alias for the SIGMA= option and the THRESHOLD= option as an alias for the THETA= option.
- GAMMA<(gamma-options)>
-
creates a gamma P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
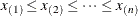
The y-coordinate of the ith point is the empirical cdf value
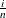 . The x-coordinate is the theoretical gamma cdf value
. The x-coordinate is the theoretical gamma cdf value
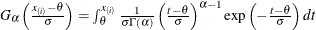 where
where 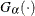 is the normalized incomplete gamma function, and
is the normalized incomplete gamma function, and 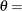 threshold parameter
threshold parameter 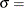 scale parameter
scale parameter 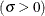
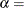 shape parameter
shape parameter 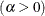
You can specify
 ,
,  , and
, and  with the ALPHA=, SIGMA=, and THETA= gamma-options, as illustrated in the following example:
with the ALPHA=, SIGMA=, and THETA= gamma-options, as illustrated in the following example:
proc capability data=measures; ppplot width / gamma(alpha=1 sigma=2 theta=3); run;
If you do not specify values for these parameters, then by default,
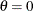 and maximum likelihood estimates are calculated for
and maximum likelihood estimates are calculated for  and
and  .
.
IMPORTANT: Your data must be greater than or equal to the lower threshold
 . If the default
. If the default 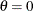 is not an adequate lower bound for your data, specify
is not an adequate lower bound for your data, specify  with the THETA= option.
with the THETA= option.
If the data are gamma distributed with parameters
 ,
,  , and
, and  , the points on the plot for ALPHA=
, the points on the plot for ALPHA= , SIGMA=
, SIGMA= , and THETA=
, and THETA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 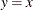 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
gamma distribution is a good fit. You can specify the SHAPE= option as an alias for the ALPHA= option, the SCALE= option as an alias for the SIGMA= option, and the THRESHOLD= option as an alias for the THETA= option.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
gamma distribution is a good fit. You can specify the SHAPE= option as an alias for the ALPHA= option, the SCALE= option as an alias for the SIGMA= option, and the THRESHOLD= option as an alias for the THETA= option.
- GUMBEL<(Gumbel-options)>
-
creates a Gumbel P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
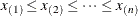
The y-coordinate of the ith point is the empirical cdf value
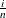 . The x-coordinate is the theoretical Gumbel cdf value
. The x-coordinate is the theoretical Gumbel cdf value
![\[ F(x_{(i)}) = \exp \left( -e^{-(x_{(i)} - \mu )/\sigma } \right) \]](images/qcug_capability0568.png)
where
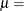 location parameter
location parameter 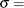 scale parameter
scale parameter 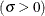
You can specify
 and
and  with the MU= and SIGMA= Gumbel-options. By default, maximum likelihood estimates are computed for
with the MU= and SIGMA= Gumbel-options. By default, maximum likelihood estimates are computed for  and
and  .
.
If the data are Gumbel distributed with parameters
 and
and  , the points on the plot for MU=
, the points on the plot for MU= and SIGMA=
and SIGMA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 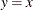 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
Gumbel distribution is a good fit.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
Gumbel distribution is a good fit.
- IGAUSS<(iGauss-options)>
-
creates an inverse Gaussian P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
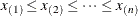
The y-coordinate of the ith point is the empirical cdf value
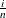 . The x-coordinate is the theoretical inverse Gaussian cdf value
. The x-coordinate is the theoretical inverse Gaussian cdf value
![\[ F(x_{(i)}) = \Phi \left\{ \sqrt {\frac{\lambda }{x_{(i)}}} \left( \frac{x_{(i)}}{\mu } - 1 \right) \right\} + e^{2\lambda /\mu } \Phi \left\{ -\sqrt {\frac{\lambda }{x_{(i)}}} \left( \frac{x_{(i)}}{\mu } + 1 \right) \right\} \]](images/qcug_capability0569.png)
where
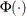 is the standard normal cumulative distribution function, and
is the standard normal cumulative distribution function, and 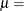 mean parameter
mean parameter 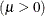
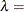 shape parameter
shape parameter 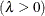
You can specify known values for
 and
and 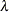 with the MU= and LAMBDA= iGauss-options. By default, the sample mean is calculated for
with the MU= and LAMBDA= iGauss-options. By default, the sample mean is calculated for  and a maximum likelihood estimate is computed for and
and a maximum likelihood estimate is computed for and 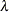 .
.
If the data are inverse Gaussian distributed with parameters
 and
and 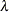 , the points on the plot for MU=
, the points on the plot for MU= and LAMBDA=
and LAMBDA=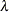 tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 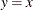 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
inverse Gaussian distribution is a good fit.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
inverse Gaussian distribution is a good fit.
- LAMBDA=value
-
specifies the shape parameter
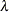 (
(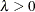 ) for P-P plots requested with the IGAUSS option. Enclose the LAMBDA= option in parentheses after the IGAUSS distribution keyword. If you do not specify a value for
) for P-P plots requested with the IGAUSS option. Enclose the LAMBDA= option in parentheses after the IGAUSS distribution keyword. If you do not specify a value for
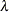 , the procedure calculates a maximum likelihood estimate.
, the procedure calculates a maximum likelihood estimate.
-
LOGNORMAL<(lognormal-options)>
LNORM<(lognormal-options)> -
creates a lognormal P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
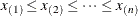
The y-coordinate of the ith point is the empirical cdf value
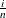 . The x-coordinate is the theoretical lognormal cdf value
. The x-coordinate is the theoretical lognormal cdf value
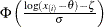 where
where 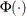 is the cumulative standard normal distribution function, and
is the cumulative standard normal distribution function, and 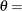 threshold parameter
threshold parameter 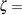 scale parameter
scale parameter 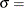 shape parameter
shape parameter 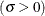
You can specify
 ,
, 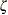 , and
, and  with the THETA=, ZETA=, and SIGMA= lognormal-options, as illustrated in the following example:
with the THETA=, ZETA=, and SIGMA= lognormal-options, as illustrated in the following example:
proc capability data=measures; ppplot width / lognormal(theta=1 zeta=2); run;
If you do not specify values for these parameters, then by default,
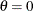 and maximum likelihood estimates are calculated for
and maximum likelihood estimates are calculated for  and
and 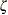 .
.
IMPORTANT: Your data must be greater than the lower threshold
 . If the default
. If the default 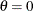 is not an adequate lower bound for your data, specify
is not an adequate lower bound for your data, specify  with the THETA= option.
with the THETA= option.
If the data are lognormally distributed with parameters
 ,
,  , and
, and 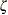 , the points on the plot for SIGMA=
, the points on the plot for SIGMA= , THETA=
, THETA= , and ZETA=
, and ZETA=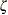 tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 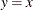 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
lognormal distribution is a good fit. You can specify the SHAPE= option as an alias for the SIGMA= option, the SCALE= option as an alias for the ZETA= option, and the THRESHOLD= option as an alias for the THETA= option.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
lognormal distribution is a good fit. You can specify the SHAPE= option as an alias for the SIGMA= option, the SCALE= option as an alias for the ZETA= option, and the THRESHOLD= option as an alias for the THETA= option.
- MU=value
-
specifies the parameter
 for a P-P plot requested with the GUMBEL, IGAUSS, and NORMAL options. For examples, see Figure 5.31, or Figure 5.32 and Figure 5.33. For the normal and inverse Gaussian distributions, the default value of
for a P-P plot requested with the GUMBEL, IGAUSS, and NORMAL options. For examples, see Figure 5.31, or Figure 5.32 and Figure 5.33. For the normal and inverse Gaussian distributions, the default value of  is the sample mean. If you do not specify a value for
is the sample mean. If you do not specify a value for  for the Gumbel distribution, the procedure calculates a maximum likelihood estimate.
for the Gumbel distribution, the procedure calculates a maximum likelihood estimate.
- NOLINE
-
NOOBSLEGEND
NOOBSL -
suppresses the legend that indicates the number of hidden observations in a legacy line printer plot. This option is ignored unless you specify the LINEPRINTER option in the PROC CAPABILITY statement.
-
NORMAL<(normal-options)>
NORM<(normal-options )> -
creates a normal P-P plot. By default, if you do not specify a distribution option, the procedure displays a normal P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
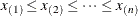
The y-coordinate of the ith point is the empirical cdf value
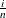 . The x-coordinate is the theoretical normal cdf value
. The x-coordinate is the theoretical normal cdf value
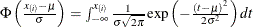 where
where 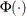 is the cumulative standard normal distribution function, and
is the cumulative standard normal distribution function, and 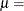 location parameter or mean
location parameter or mean 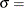 scale parameter or standard deviation
scale parameter or standard deviation 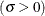
You can specify
 and
and  with the MU= and SIGMA= normal-options, as illustrated in the following example:
with the MU= and SIGMA= normal-options, as illustrated in the following example:
proc capability data=measures; ppplot width / normal(mu=1 sigma=2); run;
By default, the sample mean and sample standard deviation are used for
 and
and  .
.
If the data are normally distributed with parameters
 and
and  , the points on the plot for MU=
, the points on the plot for MU= and SIGMA=
and SIGMA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 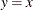 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
normal distribution is a good fit. For an example, see Figure 5.31.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
normal distribution is a good fit. For an example, see Figure 5.31.
- PARETO<(Pareto-options)>
-
creates a generalized Pareto P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
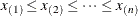
The y-coordinate of the ith point is the empirical cdf value
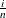 . The x-coordinate is the theoretical generalized Pareto cdf value
. The x-coordinate is the theoretical generalized Pareto cdf value
![\[ F(x_{(i)}) = 1 - { \left( 1 - \frac{\alpha (x_{(i)} - \theta )}{\sigma } \right) }^\frac {1}{\alpha } \]](images/qcug_capability0575.png)
where
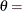 threshold parameter
threshold parameter 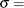 scale parameter
scale parameter 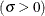
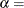 shape parameter
shape parameter
The parameter
 for the generalized Pareto distribution must be less than the minimum data value. You can specify
for the generalized Pareto distribution must be less than the minimum data value. You can specify  with the THETA= Pareto-option. The default value for
with the THETA= Pareto-option. The default value for  is 0. In addition, the generalized Pareto distribution has a shape parameter
is 0. In addition, the generalized Pareto distribution has a shape parameter  and a scale parameter
and a scale parameter  . You can specify these parameters with the ALPHA= and SIGMA= Pareto-options. By default, maximum likelihood estimates are computed for
. You can specify these parameters with the ALPHA= and SIGMA= Pareto-options. By default, maximum likelihood estimates are computed for  and
and  .
.
If the data are generalized Pareto distributed with parameters
 ,
,  , and
, and  , the points on the plot for THETA=
, the points on the plot for THETA= , SIGMA=
, SIGMA= , and ALPHA=
, and ALPHA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 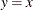 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
generalized Pareto distribution is a good fit.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
generalized Pareto distribution is a good fit.
- POWER<(power-options)>
-
creates a power function P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
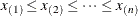
The y-coordinate of the ith point is the empirical cdf value
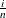 . The x-coordinate is the theoretical power function cdf value
. The x-coordinate is the theoretical power function cdf value
![\[ F(x_{(i)}) = {\left( \frac{x_{(i)} - \theta }{\sigma } \right)}^{\alpha } \]](images/qcug_capability0576.png)
where
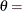 lower threshold parameter (lower endpoint)
lower threshold parameter (lower endpoint) 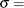 scale parameter
scale parameter 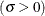
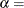 shape parameter
shape parameter 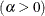
The power function distribution is bounded below by the parameter
 and above by the value
and above by the value 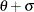 . You can specify
. You can specify  and
and  by using the THETA= and SIGMA= power-options. The default values for
by using the THETA= and SIGMA= power-options. The default values for  and
and  are 0 and 1, respectively.
are 0 and 1, respectively.
You can specify a value for the shape parameter,
 , with the ALPHA= power-option. If you do not specify a value for
, with the ALPHA= power-option. If you do not specify a value for  , the procedure calculates a maximum likelihood estimate.
, the procedure calculates a maximum likelihood estimate.
The power function distribution is a special case of the beta distribution with its second shape parameter,
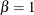 .
.
If the data are power function distributed with parameters
 ,
,  , and
, and  , the points on the plot for THETA=
, the points on the plot for THETA= , SIGMA=
, SIGMA= , and ALPHA=
, and ALPHA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 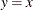 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
power function distribution is a good fit.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
power function distribution is a good fit.
- PPSYMBOL='character'
-
specifies the character used to plot the points in a legacy line printer plot. The default is the plus sign (+). This option is ignored unless you specify the LINEPRINTER option in the PROC CAPABILITY statement.
- RAYLEIGH<(Rayleigh-options)>
-
creates a Rayleigh P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
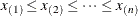
The y-coordinate of the ith point is the empirical cdf value
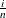 . The x-coordinate is the theoretical Rayleigh cdf value
. The x-coordinate is the theoretical Rayleigh cdf value
![\[ F(x_{(i)}) = 1 - e^{-(x_{(i)} - \theta )^2/(2\sigma ^2)} \]](images/qcug_capability0577.png)
where
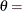 threshold parameter
threshold parameter 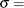 scale parameter
scale parameter 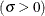
The parameter
 for the Rayleigh distribution must be less than the minimum data value. You can specify
for the Rayleigh distribution must be less than the minimum data value. You can specify  with the THETA= Rayleigh-option. The default value for
with the THETA= Rayleigh-option. The default value for  is 0. You can specify
is 0. You can specify  with the SIGMA= Rayleigh-option. By default, a maximum likelihood estimate is computed for
with the SIGMA= Rayleigh-option. By default, a maximum likelihood estimate is computed for  .
.
If the data are Rayleigh distributed with parameters
 and
and  , the points on the plot for THETA=
, the points on the plot for THETA= and SIGMA=
and SIGMA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 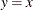 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
Rayleigh distribution is a good fit.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
Rayleigh distribution is a good fit.
- SIGMA=value
-
specifies the parameter
 , where
, where 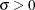 . When used with the BETA, EXPONENTIAL, GAMMA, GUMBEL, NORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options, the SIGMA= option specifies the scale parameter. When used with the LOGNORMAL option, the SIGMA= option specifies the shape parameter. Enclose the SIGMA= option in parentheses after the distribution
keyword. For an example of the SIGMA= option used with the NORMAL option, see Figure 5.31.
. When used with the BETA, EXPONENTIAL, GAMMA, GUMBEL, NORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options, the SIGMA= option specifies the scale parameter. When used with the LOGNORMAL option, the SIGMA= option specifies the shape parameter. Enclose the SIGMA= option in parentheses after the distribution
keyword. For an example of the SIGMA= option used with the NORMAL option, see Figure 5.31.
- SQUARE
-
displays the P-P plot in a square frame. The default is a rectangular frame. See Figure 5.31 for an example.
- SYMBOL='character'
-
specifies the character used for the diagonal reference line in legacy line printer plots. The default character is the first letter of the distribution option keyword. This option is ignored unless you specify the LINEPRINTER option in the PROC CAPABILITY statement.
-
THETA=value
THRESHOLD=value -
specifies the lower threshold parameter
 for plots requested with the BETA, EXPONENTIAL, GAMMA, LOGNORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options.
for plots requested with the BETA, EXPONENTIAL, GAMMA, LOGNORMAL, PARETO, POWER, RAYLEIGH, and WEIBULL options.
-
WEIBULL<(Weibull-options)>
WEIB<(Weibull-options)> -
creates a Weibull P-P plot. To create the plot, the n nonmissing observations are ordered from smallest to largest:
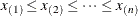
The y-coordinate of the ith point is the empirical cdf value
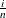 . The x-coordinate is the theoretical Weibull cdf value
. The x-coordinate is the theoretical Weibull cdf value
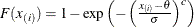 where
where 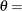 threshold parameter
threshold parameter 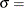 scale parameter
scale parameter 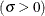 c = shape parameter (c > 0)
c = shape parameter (c > 0)
You can specify c,
 , and
, and  with the C=, SIGMA=, and THETA= Weibull-options, as illustrated in the following example:
with the C=, SIGMA=, and THETA= Weibull-options, as illustrated in the following example:
proc capability data=measures; ppplot width / weibull(theta=1 sigma=2); run;
If you do not specify values for these parameters, then by default
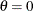 and maximum likelihood estimates are calculated for
and maximum likelihood estimates are calculated for  and c.
and c.
IMPORTANT: Your data must be greater than or equal to the lower threshold
 . If the default
. If the default 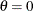 is not an adequate lower bound for your data, you should specify
is not an adequate lower bound for your data, you should specify  with the THETA= option.
with the THETA= option.
If the data are Weibull distributed with parameters c,
 , and
, and  , the points on the plot for C=c, SIGMA=
, the points on the plot for C=c, SIGMA= , and THETA=
, and THETA= tend to fall on or near the diagonal line
tend to fall on or near the diagonal line 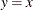 , which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
Weibull distribution is a good fit. You can specify the SHAPE= option as an alias for the C= option, the SCALE= option as
an alias for the SIGMA= option, and the THRESHOLD= option as an alias for the THETA= option.
, which is displayed by default. Agreement between the diagonal line and the point pattern is evidence that the specified
Weibull distribution is a good fit. You can specify the SHAPE= option as an alias for the C= option, the SCALE= option as
an alias for the SIGMA= option, and the THRESHOLD= option as an alias for the THETA= option.
- ZETA=value
-
specifies a value for the scale parameter
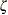 for lognormal P-P plots requested with the LOGNORMAL option.
for lognormal P-P plots requested with the LOGNORMAL option.