XCHART Statement: CUSUM Procedure
- Overview
-
Getting Started

-
Syntax

-
Details
 Basic Notation for Cusum ChartsFormulas for Cumulative SumsDefining the Decision Interval for a One-Sided Cusum SchemeDefining the V-Mask for a Two-Sided Cusum SchemeDesigning a Cusum SchemeCusum Charts Compared with Shewhart ChartsMethods for Estimating the Standard DeviationOutput Data SetsODS TablesODS GraphicsInput Data SetsMissing Values
Basic Notation for Cusum ChartsFormulas for Cumulative SumsDefining the Decision Interval for a One-Sided Cusum SchemeDefining the V-Mask for a Two-Sided Cusum SchemeDesigning a Cusum SchemeCusum Charts Compared with Shewhart ChartsMethods for Estimating the Standard DeviationOutput Data SetsODS TablesODS GraphicsInput Data SetsMissing Values -
Examples

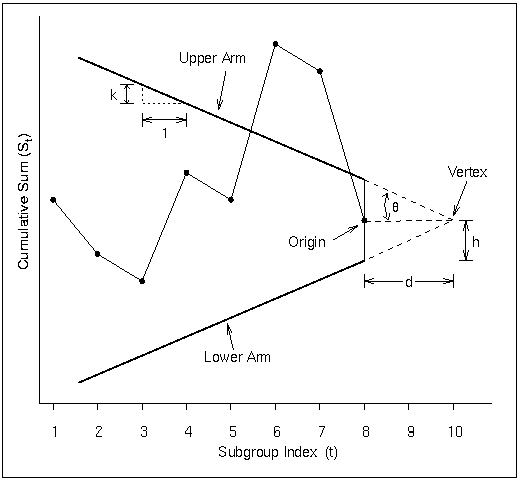
The dimensions of the V-mask can be specified using two distinct sets of two parameters.
-
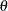 , defined as half of the angle formed by the V-mask arms, and d, the distance between the origin and the vertex, as shown in Figure 6.14. This parameterization is used by many authors, including Johnson and Leone (1962, 1974) and Montgomery (1996).
, defined as half of the angle formed by the V-mask arms, and d, the distance between the origin and the vertex, as shown in Figure 6.14. This parameterization is used by many authors, including Johnson and Leone (1962, 1974) and Montgomery (1996).
-
h, the vertical distance between the origin and the upper (or lower) V-mask arm, and k, the rise (drop) in the lower (upper) arm corresponding to an interval of one subgroup unit on the horizontal axis. You can specify the definition of an interval with the INTERVAL= option. This parameterization is used by Lucas (1976) and Wadsworth, Stephens, and Godfrey (1986). Lucas (1976) uses the symbols
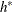 for h and
for h and 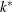 for k, and Wadsworth, Stephens, and Godfrey (1986) use the symbol f in place of k.
for k, and Wadsworth, Stephens, and Godfrey (1986) use the symbol f in place of k.
The two parameterizations are related by the equations
where the aspect ratio a is the number of units on the vertical axis corresponding to one unit on the horizontal axis. The CUSUM procedure uses the h and k parameterization because it eliminates the need for working with aspect ratios. Furthermore, h and k are also useful for average run length computations and for parameterizing one-sided cusum schemes.
You can specify the V-mask in two ways:
-
geometrically, by providing h and k (or simply h) with the H= and K= options or with the variables
_H_and_K_in a LIMITS= data set -
in terms of error probabilities, by providing
 and
and 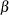 (or simply
(or simply  ) with the ALPHA= and BETA= options or with the variables
) with the ALPHA= and BETA= options or with the variables _ALPHA_and_BETA_in a LIMITS= data set. The SIGMAS= option is an alternative to the ALPHA= option, and the variable_SIGMAS_is an alternative to the variable_ALPHA_(if the READSIGMAS option is specified).
If you provide ![]() and
and ![]() , h and k are computed using the formulas
, h and k are computed using the formulas
If you provide ![]() but not
but not ![]() , h and k are computed using the formulas
, h and k are computed using the formulas
In the preceding equations, the error probability ![]() is divided by two because two-sided deviations from the target mean are detected. Refer to Johnson and Leone (1962, 1974).
is divided by two because two-sided deviations from the target mean are detected. Refer to Johnson and Leone (1962, 1974).
The origin of the V-mask is located at the most recently plotted point, as illustrated in Figure 6.14. As additional data are collected and the cumulative sum sequence is updated, the origin is relocated at the newest point. A shift or out-of-control condition is signaled at time t if one or more of the points plotted up to time t cross an arm of the V-mask. An upward shift is signaled by points crossing the lower arm, and a downward shift is signaled by points crossing the upper arm. The time at which the shift occurred corresponds to the time at which a distinct change is observed in the slope of the plotted points.