UCHART Statement: ANOM Procedure

Constructing ANOM Charts for Rates

The following notation is used in this section:

$c_{i}$

count (number of occurrences) in the ith group

k

number of groups

$n_{i}$

number of occurrence opportunity units in the ith group

N

total sample size $= n_1 + \cdots + n_ k$

$u_{i}$

occurrence rate in the ith group ($u_ i = c_ i/n_ i$)

$\bar{u}$

average of occurrence rates taken across groups. The quantity $\bar{u}$ is computed as a weighted average:

\[ \bar{u} = \frac{n_{1}u_{1} + \cdots + n_{k}u_{k}}{N} = \frac{c_{1} + \cdots + c_{k}}{N} \]

$\alpha $

significance level

$h(\alpha ;k,n,\infty )$

critical value for ANOM for normal data in the balanced case $(n_ i \equiv n)$

$h(\alpha ;k,n_1,\ldots ,n_ k,\infty )$

critical value for ANOM for normal data in the unbalanced case

Plotted Points

Each point on a u chart indicates the rate of occurrence ($u_{i}$) in a group.

Central Line

In an ANOM chart for rates, the central line represents the weighted average of the group rates, which is denoted by $\bar{u}$.

Decision Limits

For the ith group, the occurrence counts are assumed to have a Poisson distribution with parameter $\lambda _ i$. The ANOM method tests the null hypothesis that $\lambda _1 = \cdots = \lambda _ k$, that is, that the rates are the same, against the alternative that at least one of the $\lambda _ i$’s is different from the average of the k rates.

The decision limits are computed using the normal approximation to the Poisson distribution, which is appropriate when the sample sizes for the groups are large; see Ramig (1983). A commonly recommended check for this assumption is that $c_ i > 5$ for all the groups. The critical values in the ANOM method for normally distributed data are adapted to the Poisson case by using infinite degrees of freedom for the variance.

When the number of opportunity units is constant ($n_ i \equiv n$) across groups, the decision limits are computed as follow:

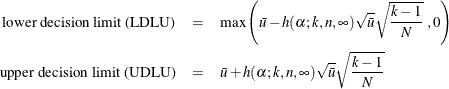
\begin{eqnarray*} \mbox{lower decision limit (LDLU)} & = & \mbox{max}\left(\bar{u} - h(\alpha ; k, n, \infty ) \sqrt {\bar{u}} \sqrt { \frac{k-1}{N}} \; ,0 \right) \\ \mbox{upper decision limit (UDLU)} & = & \bar{u} + h(\alpha ; k, n, \infty ) \sqrt {\bar{u}} \sqrt { \frac{k-1}{N}} \end{eqnarray*}

For the theoretical derivation of the decision limits, refer to Nelson (1982a).

When the number of opportunity units ($n_ i$) is different across groups (the unbalanced case), the decision limits are computed as follows:

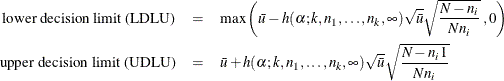
\begin{eqnarray*} \mbox{lower decision limit (LDLU)} & = & \mbox{max}\left(\bar{u} - h(\alpha ; k, n_1,\ldots ,n_ k, \infty ) \sqrt {\bar{u}} \sqrt { \frac{N-n_ i}{Nn_ i}} \; ,0 \right) \\ \mbox{upper decision limit (UDLU)} & = & \bar{u} + h(\alpha ; k, n_1,\ldots ,n_ k, \infty ) \sqrt {\bar{u}} \sqrt { \frac{N-n_ i1}{Nn_ i}} \end{eqnarray*}

Note that the decision limits for the ith group depend on $n_ i$. If the sample sizes are constant across groups ($n_ i \equiv n$), the decision limits in the unbalanced case reduce to the formulas given for the balanced case, since $n_ i \equiv n$ and $N = kn$, so

\begin{eqnarray*} \sqrt {\frac{N - n_ i}{Nn_ i}} = \sqrt {\frac{kn - n}{Nn}} = \sqrt {\frac{k - 1}{N}} \end{eqnarray*}

For the derivation of the decision limits for unequal sample sizes, refer to Nelson (1991).

Exact critical values were first tabulated by Nelson (1982a). Refer to Nelson (1993) for a derivation of the critical values $h(\alpha ;k, n, \infty )$ and Nelson (1991) for a derivation of the critical values $h(\alpha ;k, n_1,\ldots ,n_ k, \infty )$. Note that the critical values in the unequal sample size case have not been tabulated.

You can specify parameters for the limits as follows:

  • Specify $\alpha $ with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.

  • Specify a nominal constant number of opportunity units 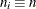$n_ i \equiv n$ with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.

  • Specify $\bar{u}$ with the U= option or with the variable _U_ in a LIMITS= data set.