The CAPABILITY Procedure

Comparison of P-P Plots and Q-Q Plots

A P-P plot compares the empirical cumulative distribution function of a data set with a specified theoretical cumulative distribution function $F(\cdot )$. A Q-Q plot compares the quantiles of a data distribution with the quantiles of a standardized theoretical distribution from a specified family of distributions. There are three important differences in the way P-P plots and Q-Q plots are constructed and interpreted:

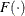  • The construction of a Q-Q plot does not require that the location or scale parameters of $F(\cdot )$ be specified. The theoretical quantiles are computed from a standard distribution within the specified family. A linear point pattern indicates that the specified family reasonably describes the data distribution, and the location and scale parameters can be estimated visually as the intercept and slope of the linear pattern. 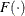In contrast, the construction of a P-P plot requires the location and scale parameters of $F(\cdot )$ to evaluate the cdf at the ordered data values.

  • The linearity of the point pattern on a Q-Q plot is unaffected by changes in location or scale. On a P-P plot, changes in location or scale do not necessarily preserve linearity.

  • On a Q-Q plot, the reference line representing a particular theoretical distribution depends on the location and scale parameters of that distribution, having intercept and slope equal to the location and scale parameters. On a P-P plot, the reference line for any distribution is always the diagonal line $y=x$.

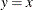Consequently, you should use a Q-Q plot if your objective is to compare the data distribution with a family of distributions that vary only in location and scale, particularly if you want to estimate the location and scale parameters from the plot.

An advantage of P-P plots is that they are discriminating in regions of high probability density, because in these regions the empirical and theoretical cumulative distributions change more rapidly than in regions of low probability density. For example, if you compare a data distribution with a particular normal distribution, differences in the middle of the two distributions are more apparent on a P-P plot than on a Q-Q plot.

For further details on P-P plots, refer to Gnanadesikan (1997) and Wilk and Gnanadesikan (1968).