XSCHART Statement: SHEWHART Procedure
Note: See Mean and Standard Deviation Charts Examples in the SAS/QC Sample Library.
A petroleum company uses a turbine to heat water into steam, which is then pumped into the ground to make oil less viscous
and easier to extract. This process occurs 20 times daily, and the amount of power (in kilowatts) used to heat the water to
the desired temperature is recorded. The following statements create a SAS data set named Turbine, which contains the power output measurements for 20 days:
data Turbine;
informat Day date7.;
format Day date5.;
input Day @;
do i=1 to 10;
input KWatts @;
output;
end;
drop i;
datalines;
04JUL94 3196 3507 4050 3215 3583 3617 3789 3180 3505 3454
04JUL94 3417 3199 3613 3384 3475 3316 3556 3607 3364 3721
05JUL94 3390 3562 3413 3193 3635 3179 3348 3199 3413 3562
05JUL94 3428 3320 3745 3426 3849 3256 3841 3575 3752 3347
06JUL94 3478 3465 3445 3383 3684 3304 3398 3578 3348 3369
06JUL94 3670 3614 3307 3595 3448 3304 3385 3499 3781 3711
07JUL94 3448 3045 3446 3620 3466 3533 3590 3070 3499 3457
... more lines ...
23JUL94 3756 3145 3571 3331 3725 3605 3547 3421 3257 3574
;
A partial listing of Turbine is shown in Figure 17.114.
Figure 17.114: Partial Listing of the Data Set Turbine
| Kilowatt Power Output Data |
| Obs | Day | KWatts |
|---|---|---|
| 1 | 04JUL | 3196 |
| 2 | 04JUL | 3507 |
| 3 | 04JUL | 4050 |
| 4 | 04JUL | 3215 |
| 5 | 04JUL | 3583 |
| 6 | 04JUL | 3617 |
| 7 | 04JUL | 3789 |
| 8 | 04JUL | 3180 |
| 9 | 04JUL | 3505 |
| 10 | 04JUL | 3454 |
| 11 | 04JUL | 3417 |
| 12 | 04JUL | 3199 |
| 13 | 04JUL | 3613 |
| 14 | 04JUL | 3384 |
| 15 | 04JUL | 3475 |
| 16 | 04JUL | 3316 |
| 17 | 04JUL | 3556 |
| 18 | 04JUL | 3607 |
| 19 | 04JUL | 3364 |
| 20 | 04JUL | 3721 |
| 21 | 05JUL | 3390 |
| 22 | 05JUL | 3562 |
| 23 | 05JUL | 3413 |
| 24 | 05JUL | 3193 |
| 25 | 05JUL | 3635 |
The data set is said to be in "strung-out" form since each observation contains the day and power output for a single heating.
The first 20 observations contain the power outputs for the first day, the second 20 observations contain the power outputs
for the second day, and so on. Because the variable Day classifies the observations into rational subgroups, it is referred to as the subgroup-variable. The variable KWatts contains the power output measurements and is referred to as the process variable (or process for short).
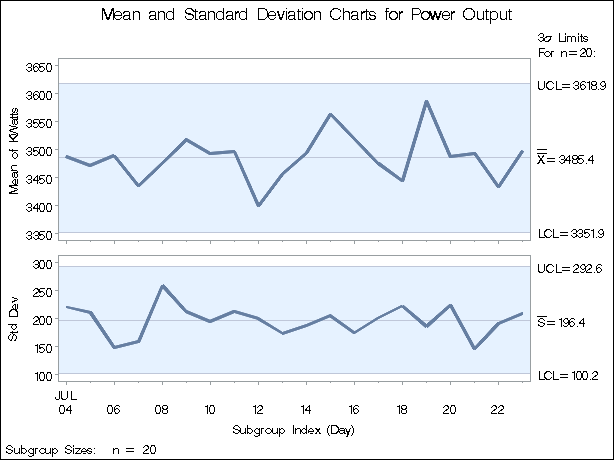
You can use ![]() and s charts to determine whether the heating process is in control. The following statements create the
and s charts to determine whether the heating process is in control. The following statements create the ![]() and s charts shown in Figure 17.115:
and s charts shown in Figure 17.115:
ods graphics off; title 'Mean and Standard Deviation Charts for Power Output'; proc shewhart data=Turbine; xschart KWatts*Day ; run;
This example illustrates the basic form of the XSCHART statement. After the keyword XSCHART, you specify the process to analyze (in this case KWatts), followed by an asterisk and the subgroup-variable (Day).
The input data set is specified with the DATA= option in the PROC SHEWHART statement.
Each point on the ![]() chart represents the mean of the measurements for a particular day. For instance, the mean plotted for the first day is
chart represents the mean of the measurements for a particular day. For instance, the mean plotted for the first day is ![]() .
.
Each point on the s chart represents the standard deviation of the measurements for a particular day. For instance, the standard deviation plotted for the first day is
Since all the points lie within the control limits, it can be concluded that the process is in statistical control.
By default, the control limits shown are ![]() limits estimated from the data; the formulas for the limits are given in Table 17.78. You can also read control limits from an input data set; see Reading Preestablished Control Limits.
limits estimated from the data; the formulas for the limits are given in Table 17.78. You can also read control limits from an input data set; see Reading Preestablished Control Limits.
For computational details, see Constructing Charts for Means and Standard Deviations. For more details on reading raw data, see DATA= Data Set.