The BOXPLOT Procedure
Percentile Definitions
You can use the PCTLDEF= option to specify one of five definitions for computing quantile statistics (percentiles). Suppose that n is the number of nonmissing values for a variable and that ![]() represent the ordered values of the analysis variable. For the tth percentile, set
represent the ordered values of the analysis variable. For the tth percentile, set ![]() .
.
For the following definitions numbered 1, 2, 3, and 5, express ![]() as
as
|
|
where j is the integer part of ![]() , and g is the fractional part of
, and g is the fractional part of ![]() . For definition 4, let
. For definition 4, let
|
|
The tth percentile (call it y) can be defined as follows:
- PCTLDEF=1
-
weighted average at
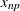
![\[ y = (1 - g)x_ j + gx_{j+1} \]](images/statug_boxplot0019.png)
where
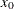 is taken to be
is taken to be 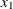 .
.
- PCTLDEF=2
-
observation numbered closest to
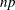
![\[ y = x_ i \]](images/statug_boxplot0022.png)
where i is the integer part of
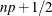 if
if 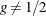 . If
. If 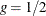 , then
, then 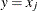 if j is even, or
if j is even, or 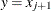 if j is odd.
if j is odd.
- PCTLDEF=3
-
empirical distribution function
![\[ y = x_ j ~ \mbox{if}~ g = 0 \]](images/statug_boxplot0028.png)
![\[ y=x_{j+1}~ \mbox{if}~ g > 0 \]](images/statug_boxplot0029.png)
- PCTLDEF=4
-
weighted average aimed at
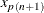
![\[ y=(1 - g)x_ j + gx_{j+1} \]](images/statug_boxplot0031.png)
where
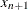 is taken to be
is taken to be 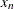 .
.
- PCTLDEF=5
-
empirical distribution function with averaging
![\[ y = (x_ j + x_{j+1})/2 ~ \mbox{if}~ g = 0 \]](images/statug_boxplot0034.png)
![\[ y = x_{j+1}~ \mbox{if}~ g > 0 \]](images/statug_boxplot0035.png)
