-
BETA=n
-
specifies the beta parameter for METHOD=FLEXIBLE. The value of n should be less than 1, usually between 0 and –1. By default, BETA=–0.25. Milligan (1987) suggests a somewhat smaller value, perhaps –0.5, for data with many outliers.
-
CCC
-
displays the cubic clustering criterion and approximate expected R square under the uniform null hypothesis (Sarle, 1983). The statistics associated with the RSQUARE option, R square and semipartial R square, are also displayed. The CCC option
applies only to coordinate data. The CCC option is not appropriate with METHOD=SINGLE because of the method’s tendency to
chop off tails of distributions. Computation of the CCC requires the eigenvalues of the covariance matrix. If the number of
variables is large, computing the eigenvalues requires much computer time and memory.
-
DATA=SAS-data-set
-
names the input data set that contains observations to be clustered. By default, the procedure uses the most recently created
SAS data set. If the data set is TYPE=DISTANCE, the data are interpreted as a distance matrix; the number of variables must
equal the number of observations in the data set or in each BY group. The distances are assumed to be Euclidean, but the procedure
accepts other types of distances or dissimilarities. If the data set is not TYPE=DISTANCE, the data are interpreted as coordinates
in a Euclidean space, and Euclidean distances are computed. For more about TYPE=DISTANCE data sets, see Appendix A: Special SAS Data Sets.
Data set types (such as TYPE=DISTANCE) do not persist when you copy or modify a data set. You must specify the TYPE= data
set option for the new data set, as in the following example:
data dist2(type=distance);
set dist;
run;
If you do not specify the TYPE=DISTANCE data set option, the new data set is the default TYPE=DATA. If you use the new data
set in a procedure that accepts both TYPE=DATA or TYPE=DISTANCE data sets (such as PROC CLUSTER or PROC MODECLUS), the results
will be incorrect.
You cannot use a TYPE=CORR data set as input to PROC CLUSTER, since the procedure uses dissimilarity measures. Instead, you
can use a DATA step or the IML procedure to extract the correlation matrix from a TYPE=CORR data set and transform the values
to dissimilarities such as 1 – r or 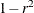 , where r is the correlation.
, where r is the correlation.
All methods produce the same results when used with coordinate data as when used with Euclidean distances computed from the
coordinates. However, the DIM= option must be used with distance data if you specify METHOD=TWOSTAGE or METHOD=DENSITY or
if you specify the TRIM= option.
Certain methods that are most naturally defined in terms of coordinates require squared Euclidean distances to be used in the combinatorial distance formulas (Lance and Williams, 1967). For this reason, distance data are automatically squared when used with METHOD=AVERAGE, METHOD=CENTROID, METHOD=MEDIAN,
or METHOD=WARD. If you want the combinatorial formulas to be applied to the (unsquared) distances with these methods, use
the NOSQUARE option.
-
DIM=n
-
specifies the dimensionality used when computing density estimates with the TRIM= option, METHOD=DENSITY, or METHOD=TWOSTAGE.
The values of n must be greater than or equal to 1. The default is the number of variables if the data are coordinates; the default is 1
if the data are distances.
-
HYBRID
-
requests the Wong (1982) hybrid clustering method in which density estimates are computed from a preliminary cluster analysis using the k-means method. The DATA= data set must contain means, frequencies, and root mean square standard deviations of the preliminary
clusters (see the FREQ and RMSSTD statements). To use HYBRID, you must use either a FREQ statement or a DATA= data set that
contains a _FREQ_ variable, and you must also use either an RMSSTD statement or a DATA= data set that contains an _RMSSTD_ variable.
The MEAN= data set produced by the FASTCLUS procedure is suitable for input to the CLUSTER procedure for hybrid clustering.
Since this data set contains _FREQ_ and _RMSSTD_ variables, you can use it as input and then omit the FREQ and RMSSTD statements.
You must specify either METHOD=DENSITY or METHOD=TWOSTAGE with the HYBRID option. You cannot use this option in combination
with the TRIM=, K=, or R= option.
-
K=n
-
specifies the number of neighbors to use for kth-nearest-neighbor density estimation (Silverman; 1986, pp. 19–21 and 96–99). The number of neighbors (n) must be at least two but less than the number of observations. See the MODE= option, which follows.
Density estimation is used with the TRIM=, METHOD=DENSITY, and METHOD=TWOSTAGE options.
-
MODE=n
-
specifies that, when two clusters are joined, each must have at least n members in order for either cluster to be designated a modal cluster. If you specify MODE=1, each cluster must also have
a maximum density greater than the fusion density in order for either cluster to be designated a modal cluster.
Use the MODE= option only with METHOD=DENSITY or METHOD=TWOSTAGE. With METHOD=TWOSTAGE, the MODE= option affects the number
of modal clusters formed. With METHOD=DENSITY, the MODE= option does not affect the clustering process but does determine
the number of modal clusters reported on the output and identified by the _MODE_ variable in the output data set.
If you specify the K= option, the default value of MODE= is the same as the value of K= because the use of kth-nearest-neighbor density estimation limits the resolution that can be obtained for clusters with fewer than k members. If you do not specify the K= option, the default is MODE=2.
If you specify MODE=0, the default value is used instead of 0.
If you specify a FREQ statement or if a _FREQ_ variable appears in the input data set, the MODE= value is compared with the number of actual observations in the clusters
being joined, not with the sum of the frequencies in the clusters.
-
NOEIGEN
-
suppresses computation of the eigenvalues of the covariance matrix and substitutes the variances of the variables for the
eigenvalues when computing the cubic clustering criterion. The NOEIGEN option saves time if the number of variables is large,
but it should be used only if the variables are nearly uncorrelated. If you specify the NOEIGEN option and the variables are
highly correlated, the cubic clustering criterion might be very liberal. The NOEIGEN option applies only to coordinate data.
-
NOID
-
suppresses the display of ID values for the clusters joined at each generation of the cluster history.
-
NONORM
-
prevents the distances from being normalized to unit mean or unit root mean square with most methods. With METHOD=WARD, the
NONORM option prevents the between-cluster sum of squares from being normalized by the total sum of squares to yield a squared
semipartial correlation. The NONORM option does not affect the reported likelihood values with METHOD=EML, but it does affect
other unrelated criteria, such as the _DIST_ variable.
-
NOPRINT
-
suppresses the display of all output. Note that this option temporarily disables the Output Delivery System (ODS). For more
information, see Chapter 20: Using the Output Delivery System.
-
NOSQUARE
-
prevents input distances from being squared with METHOD=AVERAGE, METHOD=CENTROID, METHOD=MEDIAN, or METHOD=WARD.
If you specify the NOSQUARE option with distance data, the data are assumed to be squared Euclidean distances for computing
R-square and related statistics defined in a Euclidean coordinate system.
If you specify the NOSQUARE option with coordinate data with METHOD=CENTROID, METHOD=MEDIAN, or METHOD=WARD, then the combinatorial
formula is applied to unsquared Euclidean distances. The resulting cluster distances do not have their usual Euclidean interpretation
and are therefore labeled “False” in the output.
-
NOTIE
-
prevents PROC CLUSTER from checking for ties for minimum distance between clusters at each generation of the cluster history.
If your data are measured with such precision that ties are unlikely, then you can specify the NOTIE option to reduce slightly
the time and space required by the procedure. See the section Ties for more information.
-
OUTTREE=SAS-data-set
-
creates an output data set that can be used by the TREE procedure to draw a tree diagram. If you want to create a SAS data
set in a permanent library, you must specify a two-level name. For more information about permanent libraries and SAS data
sets, see
SAS Language Reference: Concepts. If you omit the OUTTREE= option, the data set is named by using the DATAn convention and is not permanently saved. If you do not want to create an output data set, use OUTTREE=_NULL_.
-
PENALTY=p
-
specifies the penalty coefficient used with METHOD=EML. See the section Clustering Methods for more information. Values for p must be greater than zero. By default, PENALTY=2.
-
PLOTS <(global-plot-options)> <= plot-request >
PLOTS <(global-plot-options)> <= (plot-request <... plot-request >)>
-
controls the plots produced through ODS Graphics.
ODS Graphics must be enabled before plots can be requested. For example:
ods graphics on;
proc cluster method=ward plots=all;
run;
ods graphics off;
For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.
By default, PROC CLUSTER produces a dendrogram. PROC CLUSTER can also produce plots of the cubic clustering criterion, the
pseudo F statistic, and the pseudo 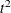 statistic from the cluster history table. These statistics are useful for estimating the number of clusters. Each statistic
is plotted against the number of clusters. You can request that PROC CLUSTER create these graphs by specifying the CCC or
PSEUDO options, or by specifying the statistics in a plot-request in the PLOT option. PROC CLUSTER might be unable to compute the statistics in some cases; for details, see the CCC and PSEUDO
options. If a statistic cannot be computed, it cannot be plotted. PROC CLUSTER plots all of these statistics that are computed
unless you tell it specifically what to plot using PLOTS=.
statistic from the cluster history table. These statistics are useful for estimating the number of clusters. Each statistic
is plotted against the number of clusters. You can request that PROC CLUSTER create these graphs by specifying the CCC or
PSEUDO options, or by specifying the statistics in a plot-request in the PLOT option. PROC CLUSTER might be unable to compute the statistics in some cases; for details, see the CCC and PSEUDO
options. If a statistic cannot be computed, it cannot be plotted. PROC CLUSTER plots all of these statistics that are computed
unless you tell it specifically what to plot using PLOTS=.
PROC CLUSTER has a CCC and PSEUDO option as well as CCC and PSEUDO plot requests. All four options are illustrated in the
following step:
ods graphics on;
proc cluster ccc pseudo plots=(ccc pseudo);
run;
ods graphics off;
The maximum number of clusters shown in all the plots is the minimum of the following quantities:
-
the number of observations
-
the value of the PRINT= option, if that option is specified
-
the maximum number of clusters for which CCC is computed, if the CCC is plotted
The global-plot-options apply to all plots generated by the CLUSTER procedure. The global-plot-options are as follows:
-
MAXCLUS=n
-
right-truncates the CCC, PSF, and PST2 plots at the n value. This prevents these plots from losing resolution when a large number of clusters are plotted. The default is MAXCLUS=200.
-
MAXPOINTS=n
MAXPTS=n
-
suppresses the dendrogram when the number of clusters exceeds the n value. This prevents an unreadable plot from being produced. The default is MAXPOINTS=200.
-
UNPACKPANEL
UNPACK
-
breaks a plot that is otherwise paneled into separate plots for each statistic.
-
ONLY
-
suppresses the default plots. Only plots specifically requested are displayed.
The following plot-requests can be specified:
-
ALL
-
generates all possible plots. The CCC and PSEUDO options must be specified to obtain the CCC, PSF and PST2 plots in addition
to the dendrogram.
-
CCC
-
implicitly specifies the CCC option and, if possible, plots the cubic clustering criterion against the number of clusters.
-
DENDROGRAM <( dendrogram-options )>
-
requests a dendrogram and specifies dendrogram-options. A dendrogram is created by default unless the ONLY global-plot-option is requested.
Unlike most graphs, the size of the dendrogram can vary as a function of the number of objects that appear in the dendrogram.
You can specify the following dendrogram-options to control the size and appearance of the dendrogram:
-
COMPUTEHEIGHT=a b
CH=a b
-
specifies the constants for computing the height of the dendrogram. For n points being clustered, intercept a, and slope b, the height is based in part on 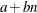 . For a horizontal dendrogram, the default (given in pixels) is COMPUTEHEIGHT=100 12, the default height in pixels is max(
. For a horizontal dendrogram, the default (given in pixels) is COMPUTEHEIGHT=100 12, the default height in pixels is max(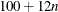 , 480), the default height in inches is max(
, 480), the default height in inches is max(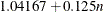 , 5), and the default height in centimeters is max(
, 5), and the default height in centimeters is max(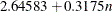 , 12.7). For a vertical dendrogram, the default height is 480 pixels. The default unit is pixels, and you can use the UNIT=
dendrogram-option to change the unit to inches or centimeters for this option. Inches equals pixels divided by 96, and centimeters equals inches
times 2.54.
, 12.7). For a vertical dendrogram, the default height is 480 pixels. The default unit is pixels, and you can use the UNIT=
dendrogram-option to change the unit to inches or centimeters for this option. Inches equals pixels divided by 96, and centimeters equals inches
times 2.54.
-
COMPUTEWIDTH=a b
CW=a b
-
specifies the constants for computing the width of the dendrogram. For n points being clustered, intercept a, and slope b, the width is based in part on 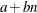 . For a vertical dendrogram, the default (given in pixels) is COMPUTEWIDTH=100 12, the default width in pixels is max(
. For a vertical dendrogram, the default (given in pixels) is COMPUTEWIDTH=100 12, the default width in pixels is max(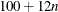 , 640), the default width in inches is max(
, 640), the default width in inches is max(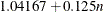 , 6.66667), and the default width in centimeters is max(
, 6.66667), and the default width in centimeters is max(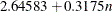 , 16.933). For a horizontal dendrogram, the default width is 640 pixels. The default unit is pixels, and you can use the UNIT=
dendrogram-option to change the unit to inches or centimeters for this option. Inches equals pixels divided by 96, and centimeters equals inches
times 2.54.
, 16.933). For a horizontal dendrogram, the default width is 640 pixels. The default unit is pixels, and you can use the UNIT=
dendrogram-option to change the unit to inches or centimeters for this option. Inches equals pixels divided by 96, and centimeters equals inches
times 2.54.
-
HEIGHT=HEIGHT | MODE | NCL | RSQ
H=H | M | N | R
-
specifies the method for drawing the height of the dendrogram. HEIGHT=HEIGHT is the default.
HEIGHT=HEIGHT specifies the distance or similarity between the last clusters joined, as defined in the section Clustering Methods.
HEIGHT=MODE pertains to the modal clusters. With METHOD=DENSITY, the mode indicates the number of modal clusters contained
by the current cluster. With METHOD=TWOSTAGE, the mode gives the maximum density in each modal cluster and the fusion density,
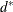 , for clusters containing two or more modal clusters; for clusters that contain no modal clusters, that value of the
, for clusters containing two or more modal clusters; for clusters that contain no modal clusters, that value of the _MODE_ variable is missing.
HEIGHT=NCL specifies that the number of clusters is used.
HEIGHT=RSQ specifies that the squared multiple correlation is used.
-
HORIZONTAL | VERTICAL
-
specifies either a horizontal dendrogram with the objects on the vertical axis (HORIZONTAL) or a vertical dendrogram with
the objects on the horizontal axis (VERTICAL). The default is HORIZONTAL.
-
SETHEIGHT=height
SH=height
-
specifies the height of the dendrogram. By default, the height is based on the COMPUTEHEIGHT= option. The default unit is
pixels, and you can use the UNIT= dendrogram-option to change the unit to inches or centimeters for this dendrogram-option.
-
SETWIDTH=width
SW=width
-
specifies the width of the dendrogram. By default, the width is based on the COMPUTEWIDTH= option. The default unit is pixels,
and you can use the UNIT= dendrogram-option to change the unit to inches or centimeters for this dendrogram-option.
-
UNIT=PX | IN | CM
-
specifies the unit (pixels, inches, or centimeters) for the SETHEIGHT=, SETWIDTH=, COMPUTEHEIGHT=, and COMPUTEWIDTH= dendrogram-options.
-
NONE
-
suppresses all plots.
-
PSEUDO
-
implicitly specifies the PSEUDO option and, if possible, plots the pseudo F statistic and the pseudo 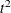 statistic against the number of clusters.
statistic against the number of clusters.
-
PSF
-
implicitly specifies the PSEUDO option and, if possible, plots the pseudo F statistic against the number of clusters.
-
PST2
-
implicitly specifies the PSEUDO option and, if possible, plots the pseudo 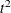 statistic against the number of clusters.
statistic against the number of clusters.
You can specify one or more of the plot requests in the same PLOT option. For example, all of the following are valid:
proc cluster plots=(ccc pst2);
proc cluster plots=(psf);
proc cluster plots=psf;
The first statement plots both the cubic clustering criterion and the pseudo 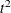 statistic, while the second and third statements plot the pseudo F statistic only. When you specify only one plot request, you can omit the parentheses around the plot request. When you specify
more than one plot request, you must specify parentheses. Otherwise the second and subsequent plot requests are options. Since
CCC and PSEUDO are both options as well as plot requests, the following three statements are valid, but they are not equivalent:
statistic, while the second and third statements plot the pseudo F statistic only. When you specify only one plot request, you can omit the parentheses around the plot request. When you specify
more than one plot request, you must specify parentheses. Otherwise the second and subsequent plot requests are options. Since
CCC and PSEUDO are both options as well as plot requests, the following three statements are valid, but they are not equivalent:
proc cluster plots(only)=ccc pseudo;
proc cluster plots(only)=pseudo ccc;
proc cluster plots(only)=(ccc pseudo);
The first two examples have one plot request and one procedure option. The third example has two plot requests.
The names of the graphs that PROC CLUSTER generates are listed in Table 31.5, along with the required statements and options.
-
PRINT=n | P=n
-
specifies the number of generations of the cluster history to display. The PRINT= option displays the latest n generations; for example, PRINT=5 displays the cluster history from one cluster through five clusters. The value of PRINT=
must be a nonnegative integer. The default is to display all generations. Specify PRINT=0 to suppress the cluster history.
-
PSEUDO
-
displays pseudo F and 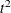 statistics. This option is effective only when the data are coordinates or when METHOD=AVERAGE, METHOD=CENTROID, or METHOD=WARD
is specified. See the section Miscellaneous Formulas for more information. The PSEUDO option is not appropriate with METHOD=SINGLE because of the method’s tendency to chop off
tails of distributions.
statistics. This option is effective only when the data are coordinates or when METHOD=AVERAGE, METHOD=CENTROID, or METHOD=WARD
is specified. See the section Miscellaneous Formulas for more information. The PSEUDO option is not appropriate with METHOD=SINGLE because of the method’s tendency to chop off
tails of distributions.
-
R=n
-
specifies the radius of the sphere of support for uniform-kernel density estimation (Silverman; 1986, pp. 11–13 and 75–94).
The value of R= must be greater than zero.
Density estimation is used with the TRIM=, METHOD=DENSITY, and METHOD=TWOSTAGE options.
-
RMSSTD
-
displays the root mean square standard deviation of each cluster. This option is effective only when the data are coordinates
or when METHOD=AVERAGE, METHOD=CENTROID, or METHOD=WARD is specified.
See the section Miscellaneous Formulas for more information.
-
RSQUARE | RSQ
-
displays the R square and semipartial R square. This option is effective only when the data are coordinates or when METHOD=AVERAGE
or METHOD=CENTROID is specified. The R square and semipartial R square statistics are always displayed with METHOD=WARD. See
the section Miscellaneous Formulas for more information..
-
SIMPLE | S
-
displays means, standard deviations, skewness, kurtosis, and a coefficient of bimodality. The SIMPLE option applies only to
coordinate data. See the section Miscellaneous Formulas for more information.
-
STANDARD | STD
-
standardizes the variables to mean 0 and standard deviation 1. The STANDARD option applies only to coordinate data.
-
TRIM=p
-
omits points with low estimated probability densities from the analysis. Valid values for the TRIM= option are 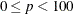 . If p < 1, then p is the proportion of observations omitted. If
. If p < 1, then p is the proportion of observations omitted. If 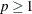 , then p is interpreted as a percentage. A specification of TRIM=10, which trims 10% of the points, is a reasonable value for many
data sets. Densities are estimated by the kth-nearest-neighbor or uniform-kernel method. Trimmed points are indicated by a negative value of the
, then p is interpreted as a percentage. A specification of TRIM=10, which trims 10% of the points, is a reasonable value for many
data sets. Densities are estimated by the kth-nearest-neighbor or uniform-kernel method. Trimmed points are indicated by a negative value of the _FREQ_ variable in the OUTTREE= data set.
You must use either the K= or R= option when you use TRIM=. You cannot use the HYBRID option in combination with TRIM=, so
you might want to use the DIM= option instead. If you specify the STANDARD option in combination with TRIM=, the variables
are standardized both before and after trimming.
The TRIM= option is useful for removing outliers and reducing chaining. Trimming is highly recommended with METHOD=WARD or
METHOD=COMPLETE because clusters from these methods can be severely distorted by outliers. Trimming is also valuable with
METHOD=SINGLE since single linkage is the method most susceptible to chaining. Most other methods also benefit from trimming.
However, trimming is unnecessary with METHOD=TWOSTAGE or METHOD=DENSITY when kth-nearest-neighbor density estimation is used.
Use of the TRIM= option can spuriously inflate the cubic clustering criterion and the pseudo F and 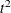 statistics. Trimming only outliers improves the accuracy of the statistics, but trimming saddle regions between clusters
yields excessively large values.
statistics. Trimming only outliers improves the accuracy of the statistics, but trimming saddle regions between clusters
yields excessively large values.
