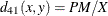Proximity Measures :: SAS/STAT(R) 12.1 User's Guide

Previous Page|Next Page

Proximity Measures

Methods That Accept All Measurement Levels
Methods That Accept Ratio, Interval, and Ordinal Variables
Methods That Accept Ratio Variables
Methods That Accept Symmetric Nominal Variables
Methods That Accept Asymmetric Nominal and Ratio Variables
Methods That Accept Asymmetric Nominal Variables

The following notation is used in this section:

v

the number of variables or the dimensionality

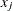
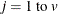
data for observation x and the jth variable, where $j = 1 \mr {\ to\ } v$

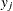
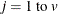
data for observation y and the jth variable, where $j = 1 \mr {\ to\ } v$

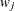
weight for the jth variable from the WEIGHTS= option in the VAR statement. 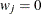when either or 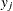is missing.

W

the sum of total weights. No matter if the observation is missing or not, its weight is added to this metric.

$\bar{x}$

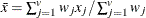
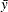
mean for observation x

$\bar{x} = \sum _{j=1}^{v}w_ j{x_ j}/\sum _{j=1}^{v}w_ j$

$\bar{y}$

mean for observation y

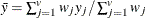
$\bar{y} = \sum _{j=1}^{v}w_ j{y_ j}/\sum _{j=1}^{v}w_ j$

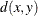
the distance or dissimilarity between observations x and y

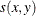
the similarity between observations x and y

The factor $W / \sum _{j=1}^{v}w_ j$ is used to adjust some of the proximity measures for missing values.

Methods That Accept All Measurement Levels

GOWER

Gower’s similarity $s_{1}(x,y) = {\sum _{j=1}^{v}w_ j\delta _{x,y}^{j}d_{x,y}^ j}/ {\sum _{j=1}^{v}w_ j\delta _{x,y}^ j}$

$\delta _{x,y}^ j$ is computed as follows:

For nominal, ordinal, interval, or ratio variable,

$\displaystyle \delta _{x,y}^ j$

$\displaystyle =$

$\displaystyle 1$

For asymmetric nominal variable,

$\displaystyle \delta _{x,y}^ j$	$\displaystyle =$	$\displaystyle 1 \mr {,\ if\ either \ } x_ j \mr {\ or\ } y_ j \mr {\ is\ present}$
$\displaystyle \delta _{x,y}^ j$	$\displaystyle =$	$\displaystyle 0 \mr {,\ if\ both \ } x_ j \mr {\ and\ } y_ j \mr {\ are\ absent}$

For nominal or asymmetric nominal variable,

$\displaystyle d_{x,y}^ j$	$\displaystyle =$	$\displaystyle 1 \mr {,\ if \ } x_ j = y_ j$
$\displaystyle d_{x,y}^ j$	$\displaystyle =$	$\displaystyle 0 \mr {,\ if \ } x_ j \neq y_ j$

For ordinal, interval, or ratio variable,

$\displaystyle d_{x,y}^ j$

$\displaystyle =$

$\displaystyle 1-|x_ j-y_ j|$

DGOWER

1 minus Gower $d_{2}(x,y) = 1 - s_{1}(x,y)$

Methods That Accept Ratio, Interval, and Ordinal Variables

EUCLID

Euclidean distance $d_{3}(x,y) = \sqrt { (\sum _{j=1}^ v{w_ j{(x_ j-y_ j)}^2}) W / (\sum _{j=1}^{v}w_ j)}$

SQEUCLID

squared Euclidean distance $d_{4}(x,y) = (\sum _{j=1}^ v{w_ j{(x_ j-y_ j)}^2}) W / (\sum _{j=1}^{v}w_ j)$

SIZE

size distance $d_{5}(x,y) = |\sum _{j=1}^ v{w_ j(x_ j-y_ j)}| \sqrt {W} / (\sum _{j=1}^{v}w_ j)$

SHAPE

shape distance $d_{6}(x,y) = \sqrt { (\sum _{j=1}^{v}w_ j[(x_ j-\bar{x})- (y_ j-\bar{y})]^2) W / (\sum _{j=1}^{v}w_ j) }$

Note: squared shape distance plus squared size distance equals squared Euclidean distance.

COV

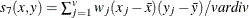covariance similarity coefficient $s_{7}(x,y) = \sum _{j=1}^{v}w_ j(x_ j-\bar{x}) (y_ j-\bar{y})/\mi {vardiv}$ , where

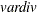
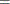
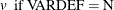
$\displaystyle \mi {vardiv }$	$\displaystyle =$	$\displaystyle v \mr {\ \ if \ VARDEF=N }$
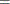
$\displaystyle$	$\displaystyle =$	$\displaystyle v-1 \mr {\ \ if \ VARDEF=DF}$
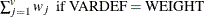
$\displaystyle$	$\displaystyle =$	$\displaystyle \textstyle \sum _{j=1}^{v}w_ j \mr {\ \ if \ VARDEF=WEIGHT}$
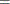
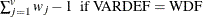
$\displaystyle$	$\displaystyle =$	$\displaystyle \textstyle \sum _{j=1}^{v}w_ j-1 \mr {\ \ if \ VARDEF=WDF}$

CORR

correlation similarity coefficient $s_{8}(x,y) = \frac{\sum _{j=1}^{v}w_ j(x_ j-\bar{x}) (y_ j-\bar{y})}{\sqrt {\sum _{j=1}^{v}w_ j(x_ j-\bar{x})^2 \sum _{j=1}^{v}w_ j(y_ j-\bar{y})^2}}$

DCORR

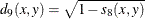
correlation transformed to Euclidean distance as sqrt(1–CORR) $d_{9}(x,y) = \sqrt {1 - s_{8}(x,y)}$

SQCORR

squared correlation $s_{10}(x,y) = \frac{[\sum _{j=1}^{v}w_ j(x_ j-\bar{x}) (y_ j-\bar{y})]^2}{\sum _{j=1}^{v}w_ j(x_ j-\bar{x})^2 \sum _{j=1}^{v}w_ j(y_ j-\bar{y})^2}$

DSQCORR

squared correlation transformed to squared Euclidean distance as (1–SQCORR)

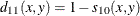
$d_{11}(x,y) = 1 - s_{10}(x,y)$

L(p)

Minkowski ( 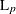$\mr {L}_ p$ ) distance, where p is a positive numeric value

$d_{12}(x,y) = [ (\sum _{j=1}^ v{w_ j{|x_ j-y_ j|}^ p}) W / (\sum _{j=1}^{v}w_ j) ]^{1/p}$

CITYBLOCK

$\mr {L}_1$ $d_{13}(x,y) = (\sum _{j=1}^ v{w_ j|x_ j-y_ j|}) W / (\sum _{j=1}^{v}w_ j)$

CHEBYCHEV

$\mr {L}_\infty$ $d_{14}(x,y) = \max _{j=1}^{v}w_ j|x_ j-y_ j|$

POWER(p,r)

generalized Euclidean distance, where p is a nonnegative numeric value and r is a positive numeric value. The distance between two observations is the rth root of sum of the absolute differences to the pth power between the values for the observations:

$d_{15}(x,y) = [ (\sum _{j=1}^ v{w_ j{|x_ j-y_ j| }^ p}) W / (\sum _{j=1}^{v}w_ j) ]^{1/r}$

Methods That Accept Ratio Variables

SIMRATIO

similarity ratio $s_{16}(x,y) = \frac{\sum _ j^{v}w_ j(x_{j}y_ j)}{\sum _{j=1}^{v}w_ j(x_{j}y_ j)+\sum _ j^{v}w_ j(x_ j-y_ j)^2}$

DISRATIO

one minus similarity ratio $d_{17}(x,y) = 1-s_{16}(x,y)$

NONMETRIC

Lance-Williams nonmetric coefficient $d_{18}(x,y) = \frac{\sum _{j=1}^{v}w_ j|x_ j-y_ j|}{\sum _{j=1}^{v}w_ j(x_ j+y_ j)}$

CANBERRA

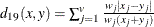
Canberra metric coefficient. See Sneath and Sokal (1973, pp. 125–126) $d_{19}(x,y) = \sum _{j=1}^{v}{\frac{{w_ j|x_ j-y_ j|}}{w_ j(x_ j+y_ j)}}$

COSINE

cosine coefficient $s_{20}(x,y) = \frac{\sum _{j=1}^{v}w_ j(x_{j}y_ j)}{\sqrt {\sum _{j=1}^{v}w_ j{x_ j}^2\sum _{j=1}^{v}w_ j{y_ j}^2}}$

DOT

dot (inner) product coefficient $s_{21}(x,y) = [\sum _{j=1}^{v}w_ j(x_{j}y_ j)]/ \sum _{j=1}^{v}w_ j$

OVERLAP

sum of the minimum values $s_{22}(x,y) = \sum _{j=1}^{v}w_ j[\min (x_ j,y_ j)]$

DOVERLAP

maximum of the sum of the x and the sum of y minus overlap $d_{23}(x,y) = \max (\sum _{j=1}^{v}w_{j}x_ j,\sum _{j=1}^{v}w_{j}y_ j)-s_{22}(x,y)$

CHISQ

chi-square If the data represent the frequency counts, chi-square dissimilarity between two sets of frequencies can be computed. A 2-by-v contingency table is illustrated to explain how the chi-square dissimilarity is computed as follows:

	Variable				Row
Observation	Var 1	Var 2	…	Var v	Sum
X			…
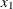
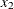
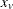
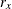
Y			…
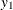
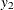
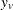
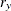
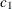
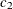
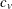
Column Sum			…		T

where

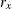
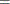
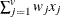
$\displaystyle r_ x$	$\displaystyle =$	$\displaystyle \textstyle \sum _{j=1}^{v}w_ jx_ j$
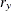
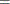
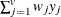
$\displaystyle r_ y$	$\displaystyle =$	$\displaystyle \textstyle \sum _{j=1}^{v}w_ jy_ j$
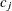
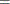
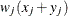
$\displaystyle c_ j$	$\displaystyle =$	$\displaystyle w_ j(x_ j+y_ j)$
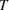
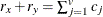
$\displaystyle T$	$\displaystyle =$	$\displaystyle r_ x+r_ y=\textstyle \sum _{j=1}^{v}c_ j$

The chi-square measure is computed as follows:

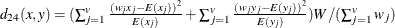
$d_{24}(x,y) = (\sum _{j=1}^ v{\frac{(w_ jx_ j-E(x_ j))^2}{E(x_ j)}}+ \sum _{j=1}^ v{\frac{(w_ jy_ j-E(y_ j))^2}{E(y_ j)}}) W / (\sum _{j=1}^{v}w_ j)$

where for j= 1, 2, …, v

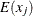
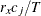
$\displaystyle E(x_ j)$	$\displaystyle =$	$\displaystyle r_ xc_ j/T$
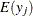
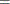
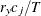
$\displaystyle E(y_ j)$	$\displaystyle =$	$\displaystyle r_ yc_ j/T$

CHI

square root of chi-square $d_{25}(x,y) = \sqrt {d_{23}(x,y)}$

PHISQ

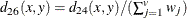
phi-square This is the CHISQ dissimilarity normalized by the sum of weights $d_{26}(x,y) = d_{24}(x,y) / (\sum _{j=1}^{v}w_ j)$

PHI

square root of phi-square $d_{27}(x,y) = \sqrt {d_{25}(x,y)}$

Methods That Accept Symmetric Nominal Variables

The following notation is used for computing $d_{28}(x,y)$ to $s_{35}(x,y)$ . Notice that only the nonmissing pairs are discussed below; all the pairs with at least one missing value will be excluded from any of the computations in the following section because $w_ j = 0 \mbox{, if either\ } x_ j \mr {\ or\ } y_ j \mbox{\ is missing.}$

M

nonmissing matches

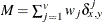$M= \sum _{j=1}^{v}w_ j\delta _{x,y}^{j}$ , where

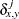
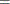
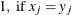
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 1 \mr {,\ if \ } x_ j = y_ j$
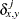
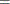
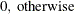
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 0 \mr {,\ otherwise}$

X

nonmissing mismatches

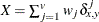$X= \sum _{j=1}^{v}w_ j\delta _{x,y}^{j}$ , where

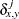
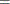
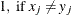
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 1 \mr {,\ if \ } x_ j \neq y_ j$
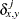
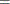
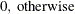
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 0 \mr {, \ otherwise}$

N

total nonmissing pairs

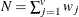
$N= \sum _{j=1}^{v}w_ j$

HAMMING: Hamming distance $d_{28}(x,y) = X$
MATCH: simple matching coefficient $s_{29}(x,y) = M/N$
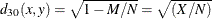
DMATCH: simple matching coefficient transformed to Euclidean distance $d_{30}(x,y) = \sqrt {1-M/N} = \sqrt {(X/N)}$
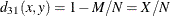
DSQMATCH: simple matching coefficient transformed to squared Euclidean distance $d_{31}(x,y) = 1-M/N = X/N$
HAMANN: Hamann coefficient $s_{32}(x,y) = (M-X) / N$
RT: Roger and Tanimoto $s_{33}(x,y) = M / (M+2X)$
SS1: Sokal and Sneath 1 $s_{34}(x,y) = 2M / (2M+X)$
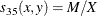
SS3: Sokal and Sneath 3. The coefficient between an observation and itself is always indeterminate (missing) since there is no mismatch. $s_{35}(x,y) = M / X$

The following notation is used for computing $s_{36}(x,y)$ to $d_{41}(x,y)$ . Notice that only the nonmissing pairs are discussed in the following section; all the pairs with at least one missing value are excluded from any of the computations in the following section because $w_ j=0 \mr {, if\ either\ } x_ j \mr {\ or\ } y_ j \mr {\ is\ missing.}$

Also, the observed nonmissing data of an asymmetric binary variable can have only two possible outcomes: presence or absence. Therefore, the notation, PX (present mismatches), always has a value of zero for an asymmetric binary variable.

The following methods distinguish between the presence and absence of attributes.

X

mismatches with at least one present

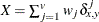$X= \sum _{j=1}^{v}w_ j\delta _{x,y}^{j}$ , where

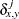
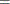
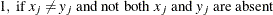
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 1 \mr {,\ if \ } x_ j \neq y_ j \mr {\ and\ not\ both \ } x_ j \mr {\ and \ } y_ j \mr {\ are\ absent}$
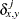
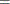
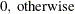
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 0 \mr {,\ otherwise}$

PM

present matches

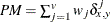$\mathit{PM}= \sum _{j=1}^{v}w_ j\delta _{x,y}^{j}$ , where

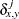
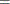
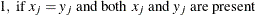
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 1 \mr {,\ if \ } x_ j = y_ j \mr {\ and\ both \ } x_ j \mr {\ and \ } y_ j \mr {\ are\ present}$
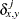
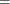
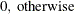
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 0 \mr {,\ otherwise}$

PX

present mismatches

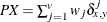$\mathit{PX}= \sum _{j=1}^{v}w_ j\delta _{x,y}^{j}$ , where

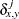
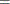
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 1 \mr {,\ if \ } x_ j \neq y_ j \mr {\ and\ both \ } x_ j \mr {\ and \ } y_ j \mr {\ are\ present}$
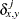
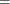
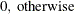
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 0 \mr {,\ otherwise}$

PP

both present = PM + PX

P

at least one present = PM + X

PAX

present-absent mismatches

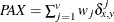$\mathit{PAX}= \sum _{j=1}^{v}w_ j\delta _{x,y}^{j}$ , where

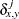
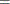
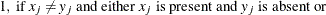
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 1 \mr {,\ if \ } x_ j \neq y_ j \mr {\ and\ either\ } x_ j \mr {\ is\ present\ and \ } y_ j \mr {\ is\ absent\ or}$
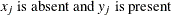
$\displaystyle$	$\displaystyle$	$\displaystyle x_ j \mr {\ is\ absent\ and \ } y_ j \mr {\ is\ present}$
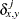
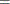
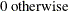
$\displaystyle \delta _{x,y}^{j}$	$\displaystyle =$	$\displaystyle 0 \mr {\ otherwise}$

N

total nonmissing pairs

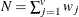
$N= \sum _{j=1}^{v}w_ j$

Methods That Accept Asymmetric Nominal and Ratio Variables

JACCARD

Jaccard similarity coefficient

The JACCARD method is equivalent to the SIMRATIO method if there are only ratio variables; if there are both ratio and asymmetric nominal variables, the coefficient is computed as sum of the coefficient from the ratio variables (SIMRATIO) and the coefficient from the asymmetric nominal variables.

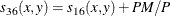
$s_{36}(x,y) = s_{16}(x,y) + \mathit{PM} / P$

DJACCARD

Jaccard dissimilarity coefficient

The DJACCARD method is equivalent to the DISRATIO method if there are only ratio variables; if there are both ratio and asymmetric nominal variables, the coefficient is computed as sum of the coefficient from the ratio variables (DISRATIO) and the coefficient from the asymmetric nominal variables.

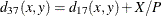
$d_{37}(x,y) = d_{17}(x,y) + X / P$

Methods That Accept Asymmetric Nominal Variables

DICE

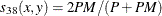
Dice coefficient or Czekanowski/Sorensen similarity coefficient $s_{38}(x,y) = 2\mathit{PM} / (P + \mathit{PM})$

RR

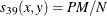
Russell and Rao. This is the binary equivalent of the dot product coefficient. $s_{39}(x,y) = \mathit{PM} / N$

BLWNM | BRAYCURTIS

Binary Lance and Williams, also known as Bray and Curtis coefficient

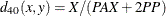
$d_{40}(x,y) = X / (\mathit{PAX}+2\mathit{PP})$

K1

Kulcynski 1. The coefficient between an observation and itself is always indeterminate (missing) since there is no mismatch. $d_{41}(x,y) = \mathit{PM} / X$

The DISTANCE Procedure