The FMM Procedure

PROBMODEL Statement

PROBMODEL <effects> </ probmodel-options> ;

The PROBMODEL statement defines the model effects for the mixing probabilities and their link function and starting values. Model effects (other than the implied intercept) are not supported with Bayesian estimation. By default, the FMM procedure models mixing probabilities on the logit scale for two-component models and as generalized logit models in situations with more than two components. The PROBMODEL statement is not required.

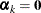The generalized logit model with k categories has a common vector of regressor or design variables, $\mb {z}$ , k – 1 parameter vectors that vary with category, and one linear predictor whose value is constant. The constant linear predictor is assigned by the FMM procedure to the last component in the model, and its value is zero ( $\balpha _{k}=\mb {0}$ ). The probability of observing category 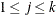$1 \leq j \leq k$ is then

$\pi _ j(\mb {z},\balpha _ j) = \frac{\exp \{ \mb {z}\balpha _ j\} }{\sum _{i=1}^ k \exp \{ \mb {z}\balpha _ i\} }$

For k=2, the generalized logit model reduces to a model with the logit link (a logistic model); hence the attribute generalized logit.

By default, an intercept is included in the model for the mixing probabilities. If you suppress the intercept with the NOINT option, you must specify at least one effect in the statement.

You can specify the following probmodel-options in the PROBMODEL statement after the slash (/):

ALPHA=number

requests that confidence intervals be constructed for the parameters in the probability model with confidence level $1-\mr {\Argument{number}}$ . The value of number must be between 0 and 1; the default is 0.05. If the probability model is simple—that is, it does not contain any effects, the confidence intervals are produced for the estimated parameters (on the logit scale) as well as for the mixing probabilities.

CL

requests that confidence limits be constructed for each of the parameter estimates. The confidence level is 0.95 by default; this can be changed with the ALPHA= option.

LINK=keyword

specifies the link function in the model for the mixing probabilities. The default is a logit link for models with two components. For models with more than two components, only the generalized logit link is available. The keywords and expressions for the associated link functions for two-component models are shown in Table 37.7.

Table 37.7: Link Functions in the PROBMODEL Statement

	Link
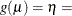
LINK=	Function	$g(\mu ) =\eta =$
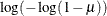
CLOGLOG \| CLL	Complementary log-log	$\log (-\log (1-\mu ))$
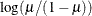
LOGIT	Logit	$\log (\mu /(1-\mu ))$
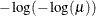
LOGLOG	Log-log	$-\log (-\log (\mu ))$
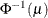
PROBIT \| NORMIT	Probit	$\Phi ^{-1}(\mu )$

NOINT

requests that no intercept be included in the model for the mixing probabilities. An intercept is included by default. If you suppress the intercept with the NOINT option, you must specify at least one other effect for the mixing probabilities—since an empty probability model is not meaningful.

PARAMETERS(parameter-specification) PARMS(parameter-specification)

specifies starting values for the parameters. The specification of the parameters takes the following form: parameters in the mean function appear in a list, and parameters for different components are separated by commas. Starting values are given on the linked scale, not in terms of probabilities. Also, you need to specify starting values for only up to the first 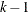components in a k-component model. The linear predictor for the last component is always assumed to be zero.

The following statements specify a three-component mixture of multiple regression models. The PROBMODEL statement does not list any effects, a standard “intercept-only” generalized logit model is used to model the mixing probabilities.

proc fmm;
   model y = x1 x2 / k=3;
   probmodel  / parms(2, 1);
run;

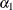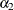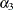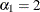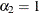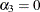There are three linear predictors in the model for the mixing probabilities, $\alpha _1$ , $\alpha _2$ , and $\alpha _3$ . With starting values of $\alpha _1 = 2$ , $\alpha _2 = 1$ , and $\alpha _3=0$ , this leads to initial mixing probabilities of

$\displaystyle \pi _1 = \frac{e^2}{e^2+e^1+e^0} = 0.24$

$\displaystyle \pi _2 = \frac{e^1}{e^2+e^1+e^0} = 0.66$

$\displaystyle \pi _3 = \frac{e^0}{e^2+e^1+e^0} = 0.1$

You can specify missing values for parameters whose starting values are to be determined by the default method.