The GAM Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Missing ValuesNonparametric RegressionAdditive Models and Generalized Additive ModelsForms of Additive ModelsEstimates from PROC GAMBackfitting and Local Scoring AlgorithmsSmoothersSelection of Smoothing ParametersConfidence Intervals for SmoothersDistribution Family and Canonical LinkDispersion ParameterComputational ResourcesODS Table NamesODS Graphics
Missing ValuesNonparametric RegressionAdditive Models and Generalized Additive ModelsForms of Additive ModelsEstimates from PROC GAMBackfitting and Local Scoring AlgorithmsSmoothersSelection of Smoothing ParametersConfidence Intervals for SmoothersDistribution Family and Canonical LinkDispersion ParameterComputational ResourcesODS Table NamesODS Graphics -
Examples

- References
Example 39.3 Comparing PROC GAM with PROC LOESS
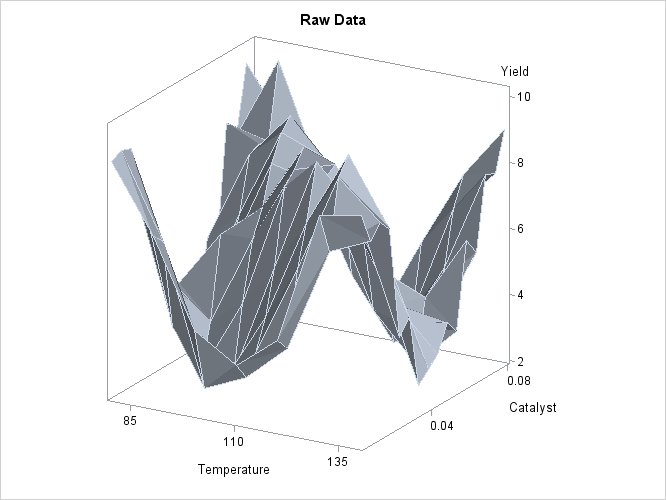
In an analysis of simulated data from a hypothetical chemistry experiment, additive nonparametric regression performed by PROC GAM is compared to the unrestricted multidimensional procedure of PROC LOESS.
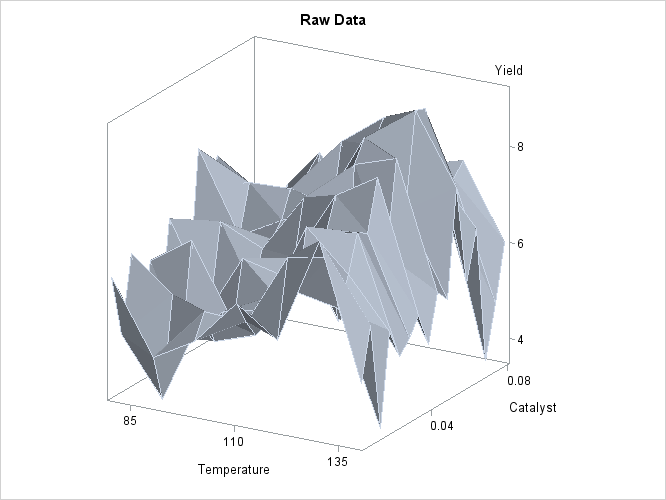
In each repetition of the experiment, a catalyst is added to a chemical solution, thereby inducing synthesis of a new material. The data are measurements of the temperature of the solution, the amount of catalyst added, and the yield of the chemical reaction. The following statements read and plots the raw data.
data ExperimentA; format Temperature f4.0 Catalyst f6.3 Yield f8.3; input Temperature Catalyst Yield @@; datalines; 80 0.005 6.039 80 0.010 4.719 80 0.015 6.301 80 0.020 4.558 80 0.025 5.917 80 0.030 4.365 80 0.035 6.540 80 0.040 5.063 80 0.045 4.668 80 0.050 7.641 80 0.055 6.736 80 0.060 7.255 80 0.065 5.515 80 0.070 5.260 80 0.075 4.813 80 0.080 4.465 90 0.005 4.540 90 0.010 3.553 90 0.015 5.611 90 0.020 4.586 90 0.025 6.503 90 0.030 4.671 90 0.035 4.919 90 0.040 6.536 90 0.045 4.799 90 0.050 6.002 90 0.055 6.988 90 0.060 6.206 90 0.065 5.193 90 0.070 5.783 90 0.075 6.482 90 0.080 5.222 100 0.005 5.042 100 0.010 5.551 100 0.015 4.804 100 0.020 5.313 100 0.025 4.957 100 0.030 6.177 100 0.035 5.433 100 0.040 6.139 100 0.045 6.217 100 0.050 6.498 100 0.055 7.037 100 0.060 5.589 100 0.065 5.593 100 0.070 7.438 100 0.075 4.794 100 0.080 3.692 110 0.005 6.005 110 0.010 5.493 110 0.015 5.107 110 0.020 5.511 110 0.025 5.692 110 0.030 5.969 110 0.035 6.244 110 0.040 7.364 110 0.045 6.412 110 0.050 6.928 110 0.055 6.814 110 0.060 8.071 110 0.065 6.038 110 0.070 6.295 110 0.075 4.308 110 0.080 7.020 120 0.005 5.409 120 0.010 7.009 120 0.015 6.160 120 0.020 7.408 120 0.025 7.123 120 0.030 7.009 120 0.035 7.708 120 0.040 5.278 120 0.045 8.111 120 0.050 8.547 120 0.055 8.279 120 0.060 8.736 120 0.065 6.988 120 0.070 6.283 120 0.075 7.367 120 0.080 6.579 130 0.005 7.629 130 0.010 7.171 130 0.015 5.997 130 0.020 6.587 130 0.025 7.335 130 0.030 7.209 130 0.035 8.259 130 0.040 6.530 130 0.045 8.400 130 0.050 7.218 130 0.055 9.167 130 0.060 9.082 130 0.065 7.680 130 0.070 7.139 130 0.075 7.275 130 0.080 7.544 140 0.005 4.860 140 0.010 5.932 140 0.015 3.685 140 0.020 5.581 140 0.025 4.935 140 0.030 5.197 140 0.035 5.559 140 0.040 4.836 140 0.045 5.795 140 0.050 5.524 140 0.055 7.736 140 0.060 5.628 140 0.065 6.644 140 0.070 3.785 140 0.075 4.853 140 0.080 6.006 ;
proc sort data=ExperimentA;
by Temperature Catalyst;
run;
proc template;
define statgraph surface;
dynamic _X _Y _Z _T;
begingraph;
entrytitle _T;
layout overlay3d/
xaxisopts=(linearopts=(tickvaluesequence=
(start=85 end=135 increment=25)))
yaxisopts=(linearopts=(tickvaluesequence=
(start=0 end=0.08 increment=0.04)))
rotate=30 cube=false;
surfaceplotparm x=_X y=_Y z=_Z;
endlayout;
endgraph;
end;
run;
ods graphics on;
proc sgrender data=ExperimentA template=surface;
dynamic _X='Temperature' _Y='Catalyst' _Z='Yield' _T='Raw Data';
run;
The plot is displayed in Output 39.3.1. A surface fitted to the plot of Output 39.3.1 by PROC LOESS will be of a very general (and flexible) type, since the procedure requires only weak assumptions about the structure of the dependencies among the data. PROC GAM, on the other hand, makes stronger structural assumptions by restricting the fitted surface to an additive form. These differences will be demonstrated in this example.
Output 39.3.1: Surface Plot of Yield by Temperature and Amount of Catalyst
The following statements request that both PROC LOESS and PROC GAM fit surfaces to the data:
ods output ScoreResults=PredLOESS;
proc loess data=ExperimentA;
model Yield = Temperature Catalyst
/ scale=sd select=gcv degree=2;
score;
run;
proc gam data=PredLoess;
model Yield = loess(Temperature) loess(Catalyst) / method=gcv;
output out=PredGAM p=Gam_p_;
run;
In both cases the smoothing parameter was chosen as the value that minimizes GCV. This is performed automatically by PROC LOESS and PROC GAM.
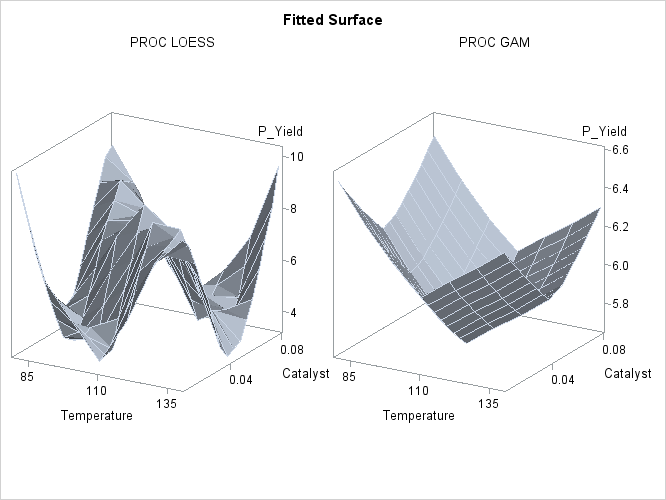
The following statements generate plots of the predicted yields, which are displayed in Output 39.3.2:
proc template;
define statgraph surface1;
begingraph;
entrytitle "Fitted Surface";
layout lattice/columns=2;
layout
overlay3d/xaxisopts=(linearopts=(tickvaluesequence=
(start=85 end=135 increment=25)))
yaxisopts=(linearopts=(tickvaluesequence=
(start=0 end=0.08 increment=0.04)))
zaxisopts=(label="P_Yield")
rotate=30 cube=0;
entry "PROC LOESS"/location=outside valign=top
textattrs=graphlabeltext;
surfaceplotparm x=Temperature y=Catalyst z=p_Yield;
endlayout;
layout
overlay3d/xaxisopts=(linearopts=(tickvaluesequence=
(start=85 end=135 increment=25)))
yaxisopts=(linearopts=(tickvaluesequence=
(start=0 end=0.08 increment=0.04)))
rotate=30 cube=0
zaxisopts=(label="P_Yield")
rotate=30 cube=0;
entry "PROC GAM"/location=outside valign=top
textattrs=graphlabeltext;
surfaceplotparm x=Temperature y=Catalyst z=Gam_p_Yield;
endlayout;
endlayout;
endgraph;
end;
run;
proc sgrender data=PredGAM template=surface1;
run;
Output 39.3.2: Fitted Regression Surfaces
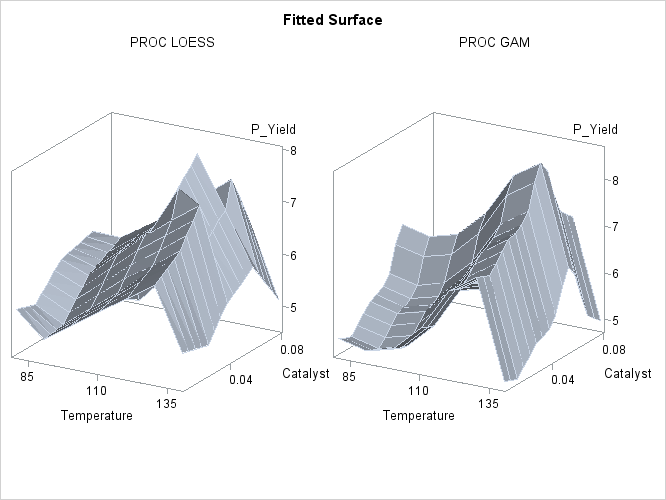
Though both PROC LOESS and PROC GAM use the statistical technique loess, it is apparent from Output 39.3.2 that the manner in which it is applied is very different. By smoothing out the data in local neighborhoods, PROC LOESS essentially fits a surface to the data in pieces, one neighborhood at a time. The local regions are treated independently, so separate areas of the fitted surface are only weakly related. PROC GAM imposes additive structure, requiring that cross sections of the fitted surface always have the same shape and thereby relating regions that have a common value of the same individual regressor variable. Under that restriction, the loess technique need not be applied to the entire multidimensional scatter plot, but only to one-dimensional cross sections of the data.
The advantage of using additive model fitting is that its statistical power is directed toward univariate smoothing, and so it is able to discern the finer details of any underlying structure in the data. Regression data can be very sparse when viewed in the context of multidimensional space, even when every individual set of regressor values densely covers its range. This is the familiar curse of dimensionality. Sparse data greatly restrict the effectiveness of nonparametric procedures, but additive model fitting, when appropriate, is one way to overcome this limitation.
To examine these properties, you can use ODS Graphics to generate plots of cross sections of the unrestricted (PROC LOESS)
and additive (PROC GAM) fitted surfaces for the variable Catalyst, as shown in the following statements:
proc template;
define statgraph projection;
begingraph;
entrytitle "Cross Sections of Fitted Surfaces";
layout lattice/rows=2 columndatarange=unionall
columngutter=10;
columnAxes;
columnAxis / display=all griddisplay=auto_on;
endColumnAxes;
layout overlay/
xaxisopts=(display=none)
yaxisopts=(label="LOESS Prediction"
linearopts=(viewmin=2 viewmax=10));
seriesplot x=Catalyst y=p_Yield /
group=temperature
name="Temperature";
endlayout;
layout overlay/
xaxisopts=(display=none)
yaxisopts=(label="GAM Prediction"
linearopts=(viewmin=2 viewmax=10));
seriesplot x=Catalyst y=Gam_p_Yield /
group=temperature
name="Temperature";
endlayout;
columnheaders;
discreteLegend "Temperature" / title = "Temperature";
endcolumnheaders;
endlayout;
endgraph;
end;
run;
proc sgrender data=PredGAM template=projection;
run;
The plots are displayed in Output 39.3.3.
Output 39.3.3: Cross Sections of Fitted Regression Surfaces
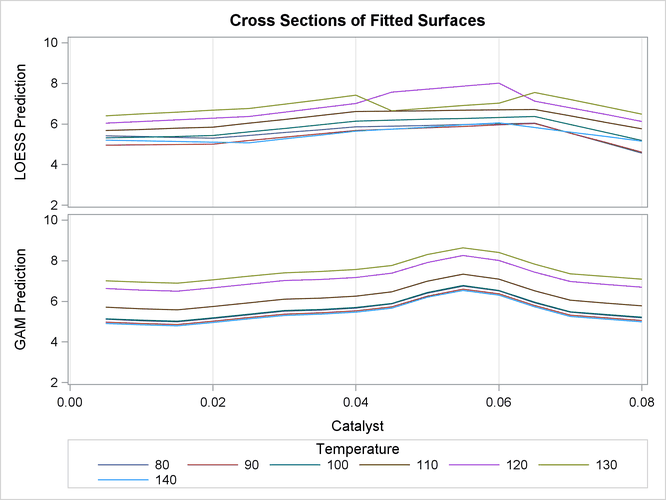
Notice that the cross sections in the top panel (PROC LOESS) of Output 39.3.3 have varying shapes, while every cross section in the bottom panel (PROC GAM) is the same curve shifted vertically. This
illustrates precisely the kind of structural differences that distinguish additive models. A second important comparison to
make between Output 39.3.2 and Output 39.3.3 is the level of detail in the fitted regression surfaces. Cross sections of the PROC LOESS surface are rather flat, but those
of the additive surface have a clear shape. In particular, the ridge near Catalyst=0.055 is only vaguely evident in the PROC LOESS surface, but it is plainly revealed by the additive procedure.
For an example of a situation where unrestricted multidimensional fitting is preferred over additive regression, consider the following simulated data from a similar experiment. The following statements create another SAS data set and plot.
data ExperimentB; format Temperature f4.0 Catalyst f6.3 Yield f8.3; input Temperature Catalyst Yield @@; datalines; 80 0.005 9.115 80 0.010 9.275 80 0.015 9.160 80 0.020 7.065 80 0.025 6.054 80 0.030 4.899 80 0.035 4.504 80 0.040 4.238 80 0.045 3.232 80 0.050 3.135 80 0.055 5.100 80 0.060 4.802 80 0.065 8.218 80 0.070 7.679 80 0.075 9.669 80 0.080 9.071 90 0.005 7.085 90 0.010 6.814 90 0.015 4.009 90 0.020 4.199 90 0.025 3.377 90 0.030 2.141 90 0.035 3.500 90 0.040 5.967 90 0.045 5.268 90 0.050 6.238 90 0.055 7.847 90 0.060 7.992 90 0.065 7.904 90 0.070 10.184 90 0.075 7.914 90 0.080 6.842 100 0.005 4.497 100 0.010 2.565 100 0.015 2.637 100 0.020 2.436 100 0.025 2.525 100 0.030 4.474 100 0.035 6.238 100 0.040 7.029 100 0.045 8.183 100 0.050 8.939 100 0.055 9.283 100 0.060 8.246 100 0.065 6.927 100 0.070 7.062 100 0.075 5.615 100 0.080 4.687 110 0.005 3.706 110 0.010 3.154 110 0.015 3.726 110 0.020 4.634 110 0.025 5.970 110 0.030 8.219 110 0.035 8.590 110 0.040 9.097 110 0.045 7.887 110 0.050 8.480 110 0.055 6.818 110 0.060 7.666 110 0.065 4.375 110 0.070 3.994 110 0.075 3.630 110 0.080 2.685 120 0.005 4.697 120 0.010 4.268 120 0.015 6.507 120 0.020 7.747 120 0.025 9.412 120 0.030 8.761 120 0.035 8.997 120 0.040 7.538 120 0.045 7.003 120 0.050 6.010 120 0.055 3.886 120 0.060 4.897 120 0.065 2.562 120 0.070 2.714 120 0.075 3.141 120 0.080 5.081 130 0.005 8.729 130 0.010 7.460 130 0.015 9.549 130 0.020 10.049 130 0.025 8.131 130 0.030 7.553 130 0.035 6.191 130 0.040 6.272 130 0.045 4.649 130 0.050 3.884 130 0.055 2.522 130 0.060 4.366 130 0.065 3.272 130 0.070 4.906 130 0.075 6.538 130 0.080 7.380 140 0.005 8.991 140 0.010 8.029 140 0.015 8.417 140 0.020 8.049 140 0.025 4.608 140 0.030 5.025 140 0.035 2.795 140 0.040 3.123 140 0.045 3.407 140 0.050 4.183 140 0.055 3.750 140 0.060 6.316 140 0.065 5.799 140 0.070 7.992 140 0.075 7.835 140 0.080 8.985 ;
proc sort data=ExperimentB; by Temperature Catalyst; run; proc sgrender data=ExperimentB template=surface; dynamic _X='Temperature' _Y='Catalyst' _Z='Yield' _T='Raw Data'; run;
A plot of the raw data is displayed in Output 39.3.4.
Output 39.3.4: Raw Data from Experiment B
Though the surface displayed in Output 39.3.4 is quite jagged, a distinct feature of the plot is a large ridge that runs diagonally across its surface. One would expect that the ridge would appear in the fitted regression surface of an appropriate nonparametric procedure. Nevertheless, between PROC LOESS and PROC GAM, only PROC LOESS is able to capture this significant feature.
The SAS program for fitting the new data is essentially the same as that for the data set from the first experiment and produces
output data set PredGAMb for this experiment. As in Output 39.3.2, multivariate and additive fitted surfaces for these data are displayed in Output 39.3.5.
Output 39.3.5: Fitted Regression Surfaces
It is clear from Output 39.3.5 that the results of PROC LOESS and PROC GAM are completely different. While the plot in the left panel resembles the raw data plot in Output 39.3.4, the plot in the right panel is essentially featureless.
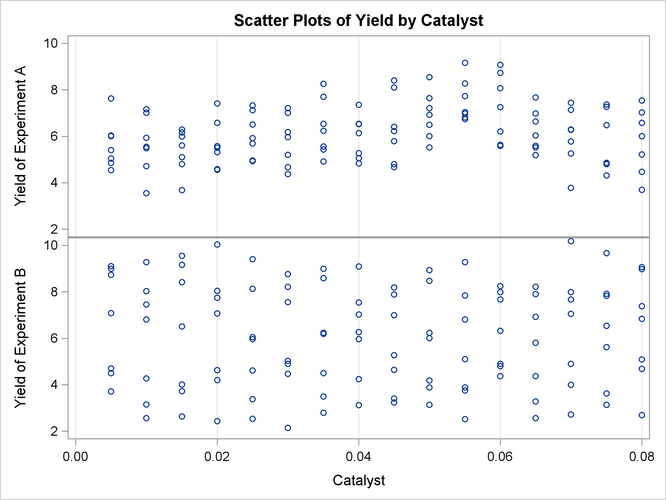
To understand what is happening, compare the scatter plots of Yield by Catalyst for the two data sets in this example. These are generated by the following statements and displayed in Output 39.3.6.
data PredGAM;
set PredGAM;
rename Yield=Yield_a;
run;
data PredGAMb;
set PredGAMb;
set PredGAM(keep=Yield_a);
run;
proc template;
define statgraph scatter2;
dynamic _X _Y1 _Y2;
begingraph;
entrytitle "Scatter Plots of Yield by Catalyst";
layout lattice/rows=2 columndatarange=unionall
rowdatarange=unionall
columngutter=15;
columnAxes;
columnAxis / display=all griddisplay=auto_on;
endColumnAxes;
layout overlay/
xaxisopts=(display=none)
yaxisopts=(label="Yield of Experiment A"
linearopts=(viewmin=2 viewmax=10));
scatterplot x=_X y=_Y1;
endlayout;
layout overlay/
xaxisopts=(display=none)
yaxisopts=(label="Yield of Experiment B"
linearopts=(viewmin=2 viewmax=10));
scatterplot x=_X y=_Y2;
endlayout;
endlayout;
endgraph;
end;
run;
proc sgrender data=PredGAMb template=scatter2;
dynamic _X='Catalyst' _Y1='Yield_a' _Y2='Yield';
run;
ods graphics off;
The top panel of Output 39.3.6 hints at the same kind of structure exhibited in the fitted cross sections of Output 39.3.3. In PROC GAM, the additive model component corresponding to Catalyst is fit to a similar scatter plot, with the partial residuals computed in the backfitting algorithm, so it is able to capture
the trend seen here. In contrast, when the second data set is viewed from the perspective of Output 39.3.6, the diagonal ridge apparent in Output 39.3.4 is washed out, and no clear structure shows up in the scatter plot. As a result, the additive model fit produced by PROC
GAM is relatively featureless.
Output 39.3.6: Scatter Plots of Yield by Catalyst