Computational Formulas :: SAS/STAT(R) 12.1 User's Guide

Computational Formulas

Breslow, Fleming-Harrington, and Kaplan-Meier Methods
Life-Table Method
Pointwise Confidence Limits in the OUTSURV= Data Set
Simultaneous Confidence Intervals for Kaplan-Meier Curves
Kernel-Smoothed Hazard Estimate
Comparison of Two or More Groups of Survival Data
Rank Tests for the Association of Survival Time with Covariates

Breslow, Fleming-Harrington, and Kaplan-Meier Methods

Let $t_1 < t_2 < \cdots < t_ D$ represent the distinct event times. For each $i=1,\ldots ,D$ , let be the number of surviving units (the size of the risk set) just prior to and let be the number of units that fail at . If the NOTRUNCATE option is specified in the FREQ statement, and can be nonintegers.

The Breslow estimate of the survivor function is

$\hat{S}(t_ i) = \exp \biggl (-\sum _{j=1}^ i \frac{d_ j}{Y_ j} \biggr )$

Note that the Breslow estimate is the exponentiation of the negative Nelson-Aalen estimate of the cumulative hazard function.

The Fleming-Harrington estimate (Fleming and Harrington, 1984) of the survivor function is

$\hat{S}(t_ i) = \exp \biggl (-\sum _{k=1}^ i\sum _{j=0}^{d_ k-1} \frac{1}{Y_ k-j} \biggr )$

If the frequency values are not integers, the Fleming-Harrington estimate cannot be computed.

The Kaplan-Meier (product-limit) estimate of the survivor function at is the cumulative product

$\hat{S}(t_ i) = \prod _{j=1}^ i \left( 1 - \frac{d_ j}{Y_ j} \right)$

Notice that all the estimators are defined to be right continuous; that is, the events at are included in the estimate of . The corresponding estimate of the standard error is computed using Greenwood’s formula (Kalbfleisch and Prentice, 1980) as

$\hat{\sigma } \left( \hat{S}(t_ i) \right) = \hat{S}(t_ i) \sqrt { \sum _{j=1}^ i \frac{d_ j}{Y_ j(Y_ j-d_ j)} } ~$

The first quartile (or the 25th percentile) of the survival time is the time beyond which 75% of the subjects in the population under study are expected to survive. It is estimated by

$q_{.25} = \mr {min}\{ t_ j | \hat{S}(t_ j) < 0.75\}$

If $\hat{S}(t)$ is exactly equal to 0.75 from to $t_{j+1}$ , the first quartile is taken to be $(t_ j + t_{j+1})/2$ . If it happens that $\hat{S}(t)$ is greater than 0.75 for all values of t, the first quartile cannot be estimated and is represented by a missing value in the printed output.

The general formula for estimating the 100p percentile point is

$q_{p} = \mr {min}\{ t_ j | \hat{S}(t_ j) < 1-p\}$

The second quartile (the median) and the third quartile of survival times correspond to p = 0.5 and p = 0.75, respectively.

Brookmeyer and Crowley (1982) have constructed the confidence interval for the median survival time based on the confidence interval for the . The methodology is generalized to construct the confidence interval for the 100p percentile based on a g-transformed confidence interval for (Klein and Moeschberger, 1997). You can use the CONFTYPE= option to specify the g-transformation. The $100(1-\alpha )$ % confidence interval for the first quantile survival time is the set of all points t that satisfy

$\biggl | \frac{ g(\hat{S}(t)) - g(1 - 0.25)}{g(\hat{S}(t)) \hat{\sigma }(\hat{S}(t))} \biggr | \leq z_{1-\frac{\alpha }{2}}$

where is the first derivative of and $z_{1-\frac{\alpha }{2}}$ is the $100(1-\frac{\alpha }{2})$ percentile of the standard normal distribution.

Consider the bone marrow transplant data described in Example 52.2. The following table illustrates the construction of the confidence limits for the first quartile in the ALL group. Values of $\frac{ g(\hat{S}(t)) - g(1 - 0.25)}{g(\hat{S}(t)) \hat{\sigma }(\hat{S}(t))}$ that lie between $\pm z_{1-\frac{0.05}{2}}$ = $\pm$ 1.965 are highlighted.

Constructing 95% Confidence Limits for the 25th Percentile
			$\frac{ g(\hat{S}(t)) - g(1 -0.25)}{g(\hat{S}(t)) \hat{\sigma }(\hat{S}(t))}$
t	$\hat{S}(t)$	$\hat{\sigma }(\hat{S}(t))$	LINEAR	LOGLOG	LOG	ASINSQRT	LOGIT
1	0.97368	0.025967	8.6141	2.37831	9.7871	4.44648	2.47903
55	0.94737	0.036224	5.4486	2.36375	6.1098	3.60151	2.46635
74	0.92105	0.043744	3.9103	2.16833	4.3257	2.94398	2.25757
86	0.89474	0.049784	2.9073	1.89961	3.1713	2.38164	1.97023
104	0.86842	0.054836	2.1595	1.59196	2.3217	1.87884	1.64297
107	0.84211	0.059153	1.5571	1.26050	1.6490	1.41733	1.29331
109	0.81579	0.062886	1.0462	0.91307	1.0908	0.98624	0.93069
110	0.78947	0.066135	0.5969	0.55415	0.6123	0.57846	0.56079
122	0.73684	0.071434	–0.1842	–0.18808	–0.1826	–0.18573	–0.18728
129	0.71053	0.073570	–0.5365	–0.56842	–0.5222	–0.54859	–0.56101
172	0.68421	0.075405	–0.8725	–0.95372	–0.8330	–0.90178	–0.93247
192	0.65789	0.076960	–1.1968	–1.34341	–1.1201	–1.24712	–1.30048
194	0.63158	0.078252	–1.5133	–1.73709	–1.3870	–1.58613	–1.66406
230	0.60412	0.079522	–1.8345	–2.14672	–1.6432	–1.92995	–2.03291
276	0.57666	0.080509	–2.1531	–2.55898	–1.8825	–2.26871	–2.39408
332	0.54920	0.081223	–2.4722	–2.97389	–2.1070	–2.60380	–2.74691
383	0.52174	0.081672	–2.7948	–3.39146	–2.3183	–2.93646	–3.09068
418	0.49428	0.081860	–3.1239	–3.81166	–2.5177	–3.26782	–3.42460
466	0.46682	0.081788	–3.4624	–4.23445	–2.7062	–3.59898	–3.74781
487	0.43936	0.081457	–3.8136	–4.65971	–2.8844	–3.93103	–4.05931
526	0.41190	0.080862	–4.1812	–5.08726	–3.0527	–4.26507	–4.35795
609	0.38248	0.080260	–4.5791	–5.52446	–3.2091	–4.60719	–4.64271
662	0.35306	0.079296	–5.0059	–5.96222	–3.3546	–4.95358	–4.90900

Consider the LINEAR transformation where . The event times that satisfy $\biggl | \frac{ g(\hat{S}(t)) - g(1 - p)}{g(\hat{S}(t)) \sqrt {\hat{V}(\hat{S}(t))}} \biggr | \leq 1.9599$ include 107, 109, 110, 122, 129, 172, 192, 194, and 230. The confidence of the interval [107, 230] is less than 95%. Brookmeyer and Crowley (1982) suggest extending the confidence interval to but not including the next event time. As such the 95% confidence interval for the first quartile based on the linear transform is [107, 276). The following table lists the confidence intervals for the various transforms.

95% CI’s for the 25th Percentile
CONFTYPE	[Lower	Upper)
LINEAR	107	276
LOGLOG	86	230
LOG	107	332
ASINSQRT	104	276
LOGIT	104	230

Sometimes, the confidence limits for the quartiles cannot be estimated. For convenience of explanation, consider the linear transform . If the curve that represents the upper confidence limits for the survivor function lies above 0.75, the upper confidence limit for first quartile cannot be estimated. On the other hand, if the curve that represents the lower confidence limits for the survivor function lies above 0.75, the lower confidence limit for the quartile cannot be estimated.

The estimated mean survival time is

$\hat{\mu } = \sum _{i=1}^ D \hat{S}(t_{i-1})(t_ i - t_{i-1})$

where is defined to be zero. When the largest observed time is censored, this sum underestimates the mean. The standard error of $\hat{\mu }$ is estimated as

$\hat{\sigma }(\hat{\mu }) = \sqrt {\frac{m}{m-1} \sum _{i=1}^{D-1} \frac{A_ i^2}{Y_ i (Y_ i - d_ i} }$

where

$\displaystyle A_ i$	$\displaystyle =$	$\displaystyle \sum _{j=i}^{D-1} \hat{S}(t_ j)(t_{j+1} - t_ j)$
$\displaystyle m$	$\displaystyle =$	$\displaystyle \sum _{j=1}^ D d_ j ~$

If the largest observed time is not an event, you can use the TIMELIM= option to specify a time limit L and estimate the mean survival time limited to the time L and its standard error by replacing k by k + 1 with $t_{k+1}=L$ .

Nelson-Aalen Estimate of the Cumulative Hazard Function

The Nelson-Aalen cumulative hazard estimator, defined up to the largest observed time on study, is

$\tilde{H}(t) = \sum _{t_ i\leq t} \frac{d_ i}{Y_ i}$

and its estimated variance is

$\hat{\sigma }^2 \left( \tilde{H}(t) \right) = \sum _{t_ i\leq t} \frac{d_ i}{Y_ i^2}$

Adjusted Kaplan-Meier Estimate

PROC LIFETEST computes the adjusted Kaplan-Meier estimate (AKME) of the survivor function if you specify both METHOD=KM and the WEIGHT statement. Let ( $T_ i,\delta _ i,w_ i), i=1,\ldots ,n,$ denote an independent sample of right-censored survival data, where is the possibly right-censored time, $\delta _ i$ is the censoring indicator ( $\delta _ i=0$ if is censored and $\delta _ i=1$ if is an event time), and is the weight (from the WEIGHT statement). Let $t_1<t_2,\ldots <t_ D$ be the D distinct event times in the sample. At time $t_ j, j=1,\ldots ,D$ , there are $d_{j}=\sum _{i}\delta _ iI(T_ i=t_ j)$ events out of $Y_{j}=\sum _{i}I(T_ i \geq t_ j)$ subjects. The weighted number of events and the weighted number at risk are $d^ w_{j} = \sum _{i} w_ i\delta _ i I(T_ i=t_ j)$ and $Y^ w_{j} = \sum _{i} w_ iI(T_ i \geq t_ j)$ , respectively. The AKME (Xie and Liu, 2005) is

$\hat{S}(t) = \left\{ \begin{array}{ll} 1 & \mbox{if $t<t_1$} \\ \prod _{t_ j \leq t} \left[ 1- \frac{d^ w_{j}}{Y^ w_{j}}\right] & \mbox{if $t \geq t_1$} \end{array} \right.$

The estimated variance of $\hat{S}(t)$ is

$\hat{\sigma }^2\left(\hat{S}(t) \right) = \left(\hat{S}(t)\right)^2 \sum _{j:t_ j \leq t} \frac{d^ w_{j}/Y^ w_{j}}{M_{j} (1-d^ w_{j}/Y^ w_{j})}$

where

$M_{j} = \frac{\left(\sum _{i:T_ i \geq t_ j} w_ i \right)^2}{ \sum _{i:T_ i \geq t_ j} w_ i^2}$

Life-Table Method

The life-table estimates are computed by counting the numbers of censored and uncensored observations that fall into each of the time intervals $[t_{i-1},t_ i)$ , $i=1,2,\ldots ,k+1$ , where and $t_{k+1}=\infty$ . Let be the number of units that enter the interval $[t_{i-1},t_ i)$ , and let be the number of events that occur in the interval. Let $b_ i=t_ i-t_{i-1}$ , and let $n_ i^{\prime }=n_ i - w_ i/2$ , where is the number of units censored in the interval. The effective sample size of the interval $[t_{i-1},t_ i)$ is denoted by $n_ i^{\prime }$ . Let $t_{mi}$ denote the midpoint of $[t_{i-1},t_ i)$ .

The conditional probability of an event in $[t_{i-1},t_ i)$ is estimated by

$\hat{q}_ i = \frac{d_ i}{n_ i^{\prime }}$

and its estimated standard error is

$\hat{\sigma } \left( \hat{q}_ i \right) = \sqrt { \frac{ \hat{q}_ i \hat{p}_ i }{ n_ i^{\prime } } }$

where $\hat{p}_ i = 1 - \hat{q}_ i$ .

The estimate of the survival function at is

$\displaystyle \hat{S}(t_ i) = \left\{ \begin{array}{ll} 1 & i=0 \\ \hat{S}(t_{i-1})p_{i-1} & i>0 \end{array} \right.$

and its estimated standard error is

$\hat{\sigma } \left( \hat{S}(t_ i) \right) = \hat{S}(t_ i) \sqrt { \sum _{j=1}^{i-1} \frac{ \hat{q}_ j }{ n_ j^{\prime } \hat{p}_ j } }$

The density function at $t_{mi}$ is estimated by

$\hat{f}(t_{mi}) = \frac{ \hat{S}(t_{i}) \hat{q}_ i }{b_ i}$

and its estimated standard error is

$\hat{\sigma } \left( \hat{f}(t_{mi}) \right) = \hat{f}(t_{mi}) \sqrt { \sum _{j=1}^{i-1} \frac{ \hat{q}_ j }{ n_ j^{\prime } \hat{p}_ j } + \frac{ \hat{p}_ i }{ n_ i^{\prime } \hat{q}_ i } }$

The estimated hazard function at $t_{mi}$ is

$\hat{h}(t_{mi}) = \frac{ 2 \hat{q}_ i }{ b_ i(1 + \hat{p}_ i) }$

and its estimated standard error is

$\hat{\sigma } \left( \hat{h}(t_{mi}) \right) = \hat{h}(t_{mi}) \sqrt { \frac{ 1 - ( b_ i \hat{h}(t_{mi})/2 )^2 }{ n_ i^{\prime } \hat{q}_ i } }$

Let $[t_{j-1},t_ j)$ be the interval in which $\hat{S}(t_{j-1}) \geq \hat{S}(t_ i)/2 > \hat{S}(t_ j)$ . The median residual lifetime at is estimated by

$\hat{M}_ i = t_{j-1} - t_ i + b_ j \frac{ \hat{S}(t_{j-1}) - \hat{S}(t_ i)/2}{ \hat{S}(t_{j-1}) - \hat{S}(t_ j) }$

and the corresponding standard error is estimated by

$\hat{\sigma }(\hat{M}_ i) = \frac{ \hat{S}(t_ i) }{ 2 \hat{f}(t_{mj}) \sqrt {n_ i^{\prime }} }$

Interval Determination

If you want to determine the intervals exactly, use the INTERVALS= option in the PROC LIFETEST statement to specify the interval endpoints. Use the WIDTH= option to specify the width of the intervals, thus indirectly determining the number of intervals. If neither the INTERVALS= option nor the WIDTH= option is specified in the life-table estimation, the number of intervals is determined by the NINTERVAL= option. The width of the time intervals is 2, 5, or 10 times an integer (possibly a negative integer) power of 10. Let $c=\log _{10}$ (maximum observed time/number of intervals), and let b be the largest integer not exceeding c. Let $d=10^{c-b}$ and let

$a = 2 \times I(d \leq 2) + 5 \times I(2 < d \leq 5) + 10 \times I(d > 5)$

with I being the indicator function. The width is then given by

$\mbox{width} = a \times 10^{b}$

By default, NINTERVAL=10.

Pointwise Confidence Limits in the OUTSURV= Data Set

Pointwise confidence limits are computed for the survivor function, and for the density function and hazard function when the life-table method is used. Let $\alpha$ be specified by the ALPHA= option. Let $z_{\alpha / 2}$ be the critical value for the standard normal distribution. That is, $\Phi (-z_{\alpha / 2}) = \alpha / 2$ , where $\Phi$ is the cumulative distribution function of the standard normal random variable.

Survivor Function

When the computation of confidence limits for the survivor function is based on the asymptotic normality of the survival estimator $\hat{S}(t)$ , the approximate confidence interval might include impossible values outside the range [0,1] at extreme values of t. This problem can be avoided by applying the asymptotic normality to a transformation of for which the range is unrestricted. In addition, certain transformed confidence intervals for perform better than the usual linear confidence intervals (Borgan and Liestøl, 1990). The CONFTYPE= option enables you to pick one of the following transformations: the log-log function (Kalbfleisch and Prentice, 1980), the arcsine-square root function (Nair, 1984), the logit function (Meeker and Escobar, 1998), the log function, and the linear function.

Let g be the transformation that is being applied to the survivor function . By the delta method, the standard error of $g(\hat{S}(t))$ is estimated by

$\tau (t) = \hat{\sigma }\left[g(\hat{S}(t))\right] = g’\left(\hat{S}(t)\right)\hat{\sigma }[\hat{S}(t)]$

where is the first derivative of the function g. The 100(1– $\alpha$ )% confidence interval for is given by

$g^{-1}\left\{ g[\hat{S}(t)] \pm z_{\frac{\alpha }{2}} g’[\hat{S}(t)]\hat{\sigma }[\hat{S}(t)] \right\}$

where $g^{-1}$ is the inverse function of g. That choices of the transformation g are as follows:

arcsine-square root transformation: The estimated variance of 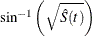$\sin ^{-1}\left(\sqrt {\hat{S}(t)}\right)$ is $\hat{\tau }^2(t) = \frac{\hat{\sigma }^2[\hat{S}(t)]}{4\hat{S}(t)[1- \hat{S}(t)] }.$ The 100(1– $\alpha$ )% confidence interval for 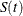is given by

$\sin ^2\left\{ \max \left[0,\sin ^{-1}(\sqrt {\hat{S}(t)}) - z_{\frac{\alpha }{2}} \hat{\tau }(t)\right]\right\} \le S(t) \le \sin ^2\left\{ \min \left[\frac{\pi }{2},\sin ^{-1}(\sqrt {\hat{S}(t)}) + z_{\frac{\alpha }{2}} \hat{\tau }(t)\right]\right\}$
linear transformation: This is the same as having no transformation in which g is the identity. The 100(1– $\alpha$ )% confidence interval for 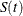is given by

$\hat{S}(t) - z_{\frac{\alpha }{2}}\hat{\sigma }\left[\hat{S}(t)\right] \le S(t) \le \hat{S}(t) + z_{\frac{\alpha }{2}}\hat{\sigma }\left[\hat{S}(t)\right]$
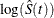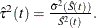log transformation: The estimated variance of $\log (\hat{S}(t))$ is $\hat{\tau }^2(t) = \frac{\hat{\sigma }^2(\hat{S}(t))}{\hat{S}^2(t)}.$ The 100(1– $\alpha$ )% confidence interval for 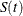is given by

$\hat{S}(t)\exp \left(-z_{\frac{\alpha }{2}}\hat{\tau }(t)\right) \le S(t) \le \hat{S}(t)\exp \left(z_{\frac{\alpha }{2}}\hat{\tau }(t)\right)$
log-log transformation: The estimated variance of 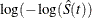$\log (-\log (\hat{S}(t))$ is $\hat{\tau }^2(t) = \frac{\hat{\sigma }^2[\hat{S}(t)]}{ [\hat{S}(t)\log (\hat{S}(t))]^2 }.$ The 100(1– $\alpha$ )% confidence interval for 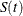is given by

$\left[\hat{S}(t)\right]^{\exp \left( z_{\frac{\alpha }{2}} \hat{\tau }(t)\right)} \le S(t) \le \left[\hat{S}(t)\right]^{\exp \left(-z_{\frac{\alpha }{2}} \hat{\tau }(t)\right)}$
logit transformation: The estimated variance of 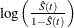$\log \left(\frac{\hat{S}(t)}{1-\hat{S}(t)}\right)$ is

$\hat{\tau }^2(t) = \frac{\hat{\sigma }^2(\hat{S}(t))}{\hat{S}^2(t)[1- \hat{S}(t)]^2}.$

The 100(1– $\alpha$ )% confidence limits for 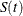are given by

$\frac{\hat{S}(t)}{\hat{S}(t) + \left[1 -\hat{S}(t) \right] \exp \left(z_{\frac{\alpha }{2}}\hat{\tau }(t)\right)} \le S(t) \le \frac{\hat{S}(t)}{\hat{S}(t) + \left[1 -\hat{S}(t) \right] \exp \left(-z_{\frac{\alpha }{2}}\hat{\tau }(t)\right)}$

Density and Hazard Functions

For the life-table method, a 100(1– $\alpha$ )% confidence interval for hazard function or density function at time t is computed as

$\hat{g}(t) \pm z_{\alpha / 2} \hat{\sigma }[\hat{g}(t)]$

where $\hat{g}(t)$ is the estimate of either the hazard function or the density function at time t, and $\hat{\sigma }[\hat{g}(t)]$ is the corresponding standard error estimate.

Simultaneous Confidence Intervals for Kaplan-Meier Curves

The pointwise confidence interval for the survivor function is valid for a single fixed time at which the inference is to be made. In some applications, it is of interest to find the upper and lower confidence bands that guarantee, with a given confidence level, that the survivor function falls within the band for all t in some interval. Hall and Wellner (1980) and Nair (1984) provide two different approaches for deriving the confidence bands. An excellent review can be found in Klein and Moeschberger (1997). You can use the CONFBAND= option in the SURVIVAL statement to select the confidence bands. The EP confidence band provides confidence bounds that are proportional to the pointwise confidence interval, while those of the HW band are not proportional to the pointwise confidence bounds. The maximum time, , for the bands can be specified by the BANDMAX= option; the minimum time, , can be specified by the BANDMIN= option. Transformations that are used to improve the pointwise confidence intervals can be applied to improve the confidence bands. It might turn out that the upper and lower bounds of the confidence bands are not decreasing in , which is contrary to the nonincreasing characteristic of survivor function. Meeker and escobar (1998) suggest making an adjustment so that the bounds do not increase: if the upper bound is increasing on the right, it is made flat from the minimum to ; if the lower bound is increasing from the right, it is made flat from to the maximum. PROC LIFETEST does not make any adjustment for the nondecreasing behavior of the confidence bands in the OUTSURV= data set. However, the adjustment was made in the display of the confidence bands by using ODS Graphics.

For Kaplan-Meier estimation, let $t_1 < t_2 < \ldots < t_ D$ be the D distinct events times, and at time , there are events. Let be the number of individuals who are at risk at time . The variance of $\hat{S}(t)$ , given by the Greenwood formula, is $\hat{\sigma }^2[\hat{S}(t)] = \sigma _ S^2(t)\hat{S}^2(t)$ , where

$\sigma _ S^2(t) = \sum _{t_ i \le t} \frac{d_ i}{Y_ i(Y_ i-d_ i)}$

Let be the time range for the confidence band so that is less than or equal to the largest event time. For the Hall-Wellner band, can be zero, but for the equal-precision band, is greater than or equal to the smallest event time. Let

$a_ L = \frac{n\sigma _ S^2(t_ L)}{1+n\sigma _ S^2(t_ L)} ~ ~ \mr {and}~ ~ a_ U = \frac{n\sigma _ S^2(t_ U)}{1+n\sigma _ S^2(t_ U)}$

Let $\{ W^0(u), 0 \le u \le 1\}$ be a Brownian bridge.

Hall-Wellner Band

The 100(1– $\alpha$ )% HW band of Hall and Wellner (1980) is

$\hat{S}(t) - h_\alpha (a_ L,a_ U) n^{-\frac{1}{2}} [1+n\sigma _ S^2(t)]\hat{S}(t) \le S(t) \le \hat{S}(t) + h_\alpha (a_ L,a_ U) n^{-\frac{1}{2}} [1+n\sigma _ S^2(t)]\hat{S}(t)$

for all $t_ L\le t \le t_ U$ , where the critical value $h_\alpha (a_ L,a_ U)$ is given by

$\alpha = \mr {Pr}\{ \sup _{a_ L \le u \le a_ U}|W^0(u)| > h_\alpha (a_ L,a_ U)\}$

The critical values are computed from the results in Chung (1986).

Note that the given confidence band has a formula similar to that of the (linear) pointwise confidence interval, where $h_{\alpha }(a_ L,a_ U)$ and $n^{-\frac{1}{2}} [1+n\sigma _ S^2(t)] \hat{S}(t)$ in the former correspond to $z_{\frac{\alpha }{2}}$ and $\hat{\sigma }(\hat{S}(t))$ in the latter, respectively. You can obtain the other transformations (arcsine-square root, log-log, log, and logit) for the confidence bands by replacing $z_{\frac{\alpha }{2}}$ and $\hat{\tau }(t)$ in the corresponding pointwise confidence interval formula by $h_\alpha (a_ L,a_ U)$ and the following $\hat{\tau }(t)$ , respectively:

arcsine-square root transformation:

$\hat{\tau }(t)= \frac{1+n\sigma _ S^2(t)}{2} \sqrt {\frac{S(t)}{n[1-S(t)]}}$
log transformation:

$\hat{\tau }(t)= \frac{1+n\sigma _ S^2(t)}{\sqrt {n}}$
log-log transformation:

$\hat{\tau }(t)= \frac{1+n\sigma _ S^2(t)}{\sqrt {n}|\log [\hat{S}(t)]|}$
logit transformation:

$\hat{\tau }(t)= \frac{1+n\sigma _ S^2(t)}{\sqrt {n}[1-\hat{S}(t)]}$

Equal-Precision Band

The 100(1– $\alpha$ )% EP band of Nair (1984) is

$\hat{S}(t) - e_\alpha (a_ L,a_ U) \hat{S}(t) \sigma _ S(t) \le S(t) \le \hat{S}(t) +e_\alpha (a_ L,a_ U) \hat{S}(t) \sigma _ S(t)$

for all $t_ L \le t \le t_ U$ , where $e_\alpha (a_ L,a_ U)$ is given by

$\alpha = \mr {Pr}\{ \sup _{a_ L \le u \le a_ U} \frac{|W^0(u)|}{[u(1-u)]^{\frac{1}{2}}} > e_\alpha (a_ L,a_ U)\}$

PROC LIFETEST uses the approximation of Miller and Siegmund (1982, Equation 8) to approximate the tail probability in which $e_\alpha (a_ L,a_ U)$ is obtained by solving x in

$\frac{4x\phi (x)}{x} + \phi (x)\left(x-\frac{1}{x}\right)\log \left[ \frac{a_ U(1-a_ L)}{a_ L(1-a_ U)}\right] = \alpha$

where $\phi (x)$ is the standard normal density function evaluated at x. Note that the confidence bounds given are proportional to the pointwise confidence intervals. As a matter of fact, this confidence band and the (linear) pointwise confidence interval have the same formula except for the critical values ( $z_{\frac{\alpha }{2}}$ for the pointwise confidence interval and $e_\alpha (a_ L,a_ U)$ for the band). You can obtain the other transformations (arcsine-square root, log-log, log, and logit) for the confidence bands by replacing $z_{\frac{\alpha }{2}}$ by $e_\alpha (a_ L,a_ U)$ in the formula of the pointwise confidence intervals.

Kernel-Smoothed Hazard Estimate

Kernel-smoothed estimators of the hazard function are based on the Nelson-Aalen estimator $\tilde{H}(t)$ and its variance $\hat{V}(\tilde{H}(t))$ . Consider the jumps of $\tilde{H}(t)$ and $\hat{V}(\tilde{H}(t))$ at the event times $t_1 < t_2 < \ldots < t_ D$ as follows:

$\displaystyle \Delta \tilde{H}(t_ i)$	$\displaystyle =$	$\displaystyle \tilde{H}(t_ i) - \tilde{H}(t_{i-1})$
$\displaystyle \hat{V}(\tilde{H}(t_ i))$	$\displaystyle =$	$\displaystyle \hat{V}(\tilde{H}(t_ i)) - \hat{V}( \tilde{H}(t_{i-1}))$

where =0.

The kernel-smoothed estimator of is a weighted average of $\Delta \tilde{H}(t)$ over event times that are within a bandwidth distance b of t. The weights are controlled by the choice of kernel function, , defined on the interval [–1,1]. The choices are as follows:

uniform kernel:

$K_ U(x) = \frac{1}{2}, ~ ~ -1\leq x \leq 1\\$
Epanechnikov kernel:

$K_ E(x) = \frac{3}{4}(1-x^2), ~ ~ -1\leq x \leq 1$
biweight kernel:

$K_{\mi {BW}}(x) = \frac{15}{16}(1-x^2)^2, ~ ~ -1\leq x \leq 1$

The kernel-smoothed hazard rate estimator is defined for all time points on . For time points t for which $b \leq t \leq t_ D -b$ , the kernel-smoothed estimated of based on the kernel is given by

$\hat{h}(t) = \frac{1}{b} \sum _{i=1}^ D K \biggl (\frac{t-t_ i}{b} \biggr ) \Delta \tilde{H}(t_ i)$

The variance of $\hat{h}(t)$ is estimated by

$\hat{\sigma ^2}(\hat{h}(t)) = \frac{1}{b^2} \sum _{i=1}^ D K\biggl (\frac{t-t_ i}{b} \biggr )^2 \Delta \hat{V}(\tilde{H}(t_ i))$

For t < b, the symmetric kernels are replaced by the corresponding asymmetric kernels of Gasser and Müller (1979). Let $q=\frac{t}{b}$ . The modified kernels are as follows:

uniform kernel:

$K_{U,q}(x) = \frac{4(1+q^3)}{(1+q)^4} + \frac{6(1-q)}{(1+q)^3}x, ~ ~ ~ -1 \leq x \leq q$
Epanechnikov kernel:

$K_{E,q}(x)= K_ E(x) \frac{64(2-4q+6q^2-3q^3) + 240(1-q)^2 x }{ (1+q)^4(19-18q+3q^2)}, ~ ~ -1 \leq x \leq q$
biweight kernel:

$K_{\mi {BW},q}(x) = K_{\mi {BW}}(x) \frac{64(8-24q+48q^2-45q^3+15q^4) + 1120(1-q)^3 x}{(1+q)^5(81-168q+126q^2-40q^3+5q^4)}, ~ ~ -1\leq x \leq q$

For $t_ D -b \leq t \leq t_ D$ , let $q=\frac{t_ D - t}{b}$ . The asymmetric kernels for are used with x replaced by –x.

Using the log transform on the smoothed hazard rate, the 100(1– $\alpha$ )% pointwise confidence interval for the smoothed hazard rate is given by

$\hat{h}(t) = \hat{h}(t)\exp \biggl [\pm \frac{z_{1-\alpha /2} \hat{\sigma }(\hat{h}(t))}{\hat{h}(t)} \biggr ]$

where $z_{1-\frac{\alpha }{2}}$ is the 100(1– $\frac{\alpha }{2}$ )th percentile of the standard normal distribution.

Optimal Bandwidth

The following mean integrated squared error (MISE) over the range $\tau _ L$ and $\tau _ U$ is used as a measure of the global performance of the kernel function estimator:

$\displaystyle \mbox{MISE}(b)$	$\displaystyle =$	$\displaystyle E \int _{\tau _ L}^{\tau _ U} (\hat{h}(i) - h(u))^2 du$
$\displaystyle$	$\displaystyle =$	$\displaystyle E\int _{\tau _ L}^{\tau _ U} \hat{h}^2(u)du - 2E \int _{\tau _ L}^{\tau _ U} \hat{h}(u)h(u)du + E\int _{\tau _ L}^{\tau _ U} h^2(u)du$

The last term is independent of the choice of the kernel and bandwidth and can be ignored when you are looking for the best value of b. The first integral can be approximated by using the trapezoid rule by evaluating $\hat{h}(t)$ at a grid of points $\tau _ L=u_1 < \ldots < u_ M=\tau _ U$ . You can specify $\tau _ L, \tau _ R$ , and M by using the options GRIDL=, GRIDU=, and NMINGRID=, respectively, of the HAZARD plot. The second integral can be estimated by the Ramlau-Hansen (1983a, 1983b) cross-validation estimate:

$\frac{1}{b} \sum _{i \neq j} K\biggl ( \frac{t_ i-t_ j}{b} \biggr ) \Delta \hat{H}(t_ i) \Delta \hat{H}(t_ j)$

Therefore, for a fixed kernel, the optimal bandwidth is the quantity b that minimizes

$g(b) = \sum _{i=1}^{M-1} \biggl [\frac{u_{i+1} - u_ k}{2} \biggl (\hat{h}^2(u_ i) + \hat{h}^2(u_{i+1}) \biggr )\biggr ] - \frac{2}{b} \sum _{i \neq j} K\biggl ( \frac{t_ i-t_ j}{b} \biggr ) \Delta \hat{H}(t_ i) \Delta \hat{H}(t_ j)$

The minimization is carried out by the golden section search algorithm.

Comparison of Two or More Groups of Survival Data

Let K be the number of groups. Let be the underlying survivor function of the kth group, $k=1,\ldots ,K$ . The null and alternative hypotheses to be tested are

$H_0: S_1(t)= S_2(t) = \ldots = S_ K(t)$ for all $t\le \tau$

versus

at least one of the ’s is different for some $t\le \tau$

respectively, where $\tau$ is the largest observed time.

Likelihood Ratio Test

The likelihood ratio test statistic (Lawless, 1982) for test versus assumes that the data in the various samples are exponentially distributed and tests that the scale parameters are equal. The test statistic is computed as

$\chi ^2 = 2N \log \left( \frac{T}{N} \right) - 2 \sum _{k=1}^ K N_ k \log \left( \frac{T_ k}{N_ k} \right)$

where is the total number of events in the kth group, $N = \sum _{k=1}^ k N_ k$ , is the total time on test in the kth stratum, and $T = \sum _{k=1}^ K T_ k$ . The approximate probability value is computed by treating $\chi ^2$ as having a chi-square distribution with K – 1 degrees of freedom.

Nonparametric Tests

Let ( $T_ i,\delta _ i,X_ i), i=1,\ldots ,n,$ denote an independent sample of right-censored survival data, where is the possibly right-censored time, $\delta _ i$ is the censoring indicator ( $\delta _ i$ =0 if is censored and $\delta _ i$ =1 if is an event time), and $X_ i=1,\ldots ,K$ for K different groups. Let $t_1<t_2<\ldots <t_ D$ be the distinct event times in the sample. At time $t_ j, j=1,\ldots ,D,$ let be a positive weight function, and let $Y_{jk}=\sum _{i:T_ i\geq t_ j}I(Xi=k)$ and $d_{jk}=\sum _{i:T_ i=t_ j}\delta _ iI(X_ i=k)$ be the size of the risk set and the number of events in the kth group, respectively. Let $Y_ j = \sum _{k=1}^ K Y_{jk}$ , $d_ j=\sum _{k=1}^ K d_{jk}$ .

The choices of the weight function are given in Table 52.4.

Table 52.4: Weight Functions for Various Tests

Test
Log-rank	1.0
Wilcoxon
Tarone-Ware	$\sqrt {Y_ j}$
Peto-Peto	$\tilde{S}(t_ j)$
Modified Peto-Peto	$\tilde{S}(t_ j) \frac{Y_ j}{Y_ j+1}$
Harrington-Fleming (p,q)	$[\hat{S}(t_ j)]^ p[1-\hat{S}(t_ j)]^ q, p\ge 0, q\ge 0$

In Table 52.4, $\hat{S}(t)$ is the product-limit estimate at t for the pooled sample, and $\tilde{S}(t)$ is a survivor function estimate close to $\hat{S}(t)$ given by

$\tilde{S}(t) = \prod _{t_ j\le t} \biggl (1 - \frac{d_ j}{Y_ j+1} \biggr )$

Unstratified Tests

The rank statistics (Klein and Moeschberger, 1997, Section 7.3) for testing versus have the form of a K-vector $\mb {v}=(v_1,v_2,\ldots ,v_ K)^{\prime }$ with

$v_ k = \sum _{j=1}^ D \left[W(t_ j) \left( d_{jk} - Y_{jk}\frac{d_ j}{Y_ j} \right) \right]$

and the variance of and the covariance of and are, respectively,

$\displaystyle V_{kk}$	$\displaystyle =$	$\displaystyle \sum _{j=1}^ D \left[W^2(t_ j) \frac{ d_ j (Y_ j-d_ j) Y_{jk} (Y_ j - Y_{jk})}{ Y_ j^2 (Y_ j - 1) } \right], \mbox{~ ~ ~ } 1\leq k \leq K$
$\displaystyle V_{kh}$	$\displaystyle =$	$\displaystyle -\sum _{j=1}^ D \left[W^2(t_ j) \frac{ d_ j (Y_ j-d_ j) Y_{jk} Y_{jh} }{ Y_ j^2 (Y_ j - 1) }\right], \mbox{~ ~ ~ } 1 \leq k \neq h \leq K$

The statistic can be interpreted as a weighted sum of observed minus expected numbers of failure for the kth group under the null hypothesis of identical survival curves. Let $\bV =(V_{kh})$ . The overall test statistic for homogeneity is $\mb {v}^{\prime }\mb {V^{-}v}$ , where $\mb {V^{-}}$ denotes a generalized inverse of $\mb {V}$ . This statistic is treated as having a chi-square distribution with degrees of freedom equal to the rank of $\mb {V}$ for the purposes of computing an approximate probability level.

Adjusted Log-Rank Test

PROC LIFETEST computes the weighted log-rank test (Xie and Liu, 2005, 2011) if you specify the WEIGHT statement. Let ( $T_ i,\delta _ i,X_ i,w_ i), i=1,\ldots ,n,$ denote an independent sample of right-censored survival data, where is the possibly right-censored time, $\delta _ i$ is the censoring indicator ( $\delta _ i$ =0 if is censored and $\delta _ i$ =1 if is an event time), $X_ i=1,\ldots ,K$ for K different groups, and is the weight from the WEIGHT statement. Let $t_1<t_2<\ldots <t_ D$ be the distinct event times in the sample. At each $t_ j, j=1,\ldots ,D$ , and for each $1\leq k \leq K$ , let

$\displaystyle d_{jk}= \sum _{i:T_ i=t_ j} I(X_ i=k)$	$\displaystyle$	$\displaystyle d_{jk}^ w=\sum _{i:T_ i=t_ j} w_ iI(X_ i=k)$
$\displaystyle Y_{jk}=\sum _{i:T_ i\geq t_ j} I(X_ i=k)$	$\displaystyle$	$\displaystyle Y_{jk}^ w=\sum _{i:T_ i\geq t_ j} w_ iI(X_ i=k)$

Let $d_ j = \sum _{k=1}^ K d_{jk}$ and $Y_ j= \sum _{k=1}^ K Y_{jk}$ denote the number of events and the number at risk, respectively, in the combined sample at time . Similarly, let $d^ w_ j = \sum _{k=1}^ K d^ w_{jk}$ and $Y^ w_ j= \sum _{k=1}^ K Y^ w_{jk}$ denote the weighted number of events and the weighted number at risk, respectively, in the combined sample at time . The test statistic is

$v_ k= \sum _{j=1}^ D \left( d^ w_{jk} - Y^ w_{jk} \frac{d^ w_ j}{Y^ w_ j} \right) \mbox{~ ~ }k= 1, \ldots , K$

and the variance of and the covariance of and are, respectively,

$\displaystyle {V}_{kk}$	$\displaystyle =$	$\displaystyle \sum _{j=1}^ D \left\{ \frac{d_ j(Y_ j-d_ j)}{Y_ j(Y_ j-1)} \sum _{i=1}^{Y_ j} \left[ \left( \frac{Y^ w_{jk}}{Y^ w_ j }\right)^2 w^2_ iI\{ X_ i\neq k\} + \left( \frac{Y^ w_ j - Y^ w_{jk}}{Y^ w_ j }\right)^2 w^2_ i I\{ X_ i=k\} \right] \right\} , \mbox{~ ~ ~ } 1\leq k \leq K$
$\displaystyle {V}_{kh}$	$\displaystyle =$	$\displaystyle \sum _{j=1}^ D \left\{ \frac{d_ j(Y_ j-d_ j)}{Y_ j(Y_ j-1)} \sum _{i=1}^{Y_ j} \left[ \frac{Y^ w_{jk} Y^ w_{jh}}{(Y^ w_ j)^2} w^2_ iI\{ X_ i\neq k, h\} - \frac{(Y^ w_ j - Y^ w_{jk})Y^ w_{jh}}{(Y^ w_ j)^2} w^2_ i I\{ X_ i=k\} \right. \right.$
$\displaystyle$	$\displaystyle$	$\displaystyle \left. \left. - \frac{(Y^ w_ j - Y^ w_{jh})Y^ w_{jk}}{(Y^ w_ j)^2} w^2_ i I\{ X_ i=h\} \right] \right\} , \mbox{~ ~ ~ } 1 \leq k \neq h \leq K$

Let ${V}= ({V}_{kh})$ . Under , the weighted K-sample test has a $\chi ^2$ statistic given by

$\chi ^2= (v_1,\ldots ,v_ K) \bV ^{-} (v_1,\ldots ,v_ K)’$

with K – 1 degrees of freedom.

Stratified Tests

Suppose the test is to be stratified on M levels of a set of STRATA variables. Based only on the data of the sth stratum ( $s=1 \dots M$ ), let $\mb {v}_ s$ be the test statistic (Klein and Moeschberger, 1997, Section 7.5) for the sth stratum, and let $\bV _ s$ be its covariance matrix. Let

$\displaystyle \mb {v}$	$\displaystyle =$	$\displaystyle \sum _{s=1}^ M \mb {v}_ s$
$\displaystyle \bV$	$\displaystyle =$	$\displaystyle \sum _{s=1}^ M \bV _ s$

A global test statistic is constructed as

$\chi ^2 = \mb {v}’ \bV ^{-} \mb {v}$

Under the null hypothesis, the test statistic has a $\chi ^2$ distribution with the same degrees of freedom as the individual test for each stratum.

Multiple-Comparison Adjustments

Let $\chi ^2_ r$ denote a chi-square random variable with r degrees of freedom. Denote $\phi$ and $\Phi$ as the density function and the cumulative distribution function of a standard normal distribution, respectively. Let m be the number of comparisons; that is,

$\displaystyle m = \left\{ \begin{array}{ll} \frac{k(k-1)}{2} & \mr {DIFF=ALL} \\ k-1 & \mr {DIFF=CONTROL} \end{array} \right.$

For a two-sided test that compares the survival of the jth group with that of lth group, $1\leq j \neq l \leq r$ , the test statistic is

$z^2_{jl}= \frac{(v_ j - v_ l)^2}{V_{jj} + V_{ll} - 2V_{jl}}$

and the raw p-value is

$p = \mr {Pr}(\chi ^2_1 > z^2_{jl})$

Adjusted p-values for various multiple-comparison adjustments are computed as follows:

Bonferroni adjustment:

$p = \mr {min}\{ 1, m \mr {Pr}(\chi ^2_1 > z^2_{jl})\}$
Dunnett-Hsu adjustment: With the first group being the control, let 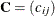$\bC =(c_{ij})$ be the 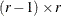$(r-1)\times r$ matrix of contrasts; that is,

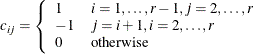
$\displaystyle c_{ij} = \left\{ \begin{array}{ll} 1 & i=1,\ldots ,r-1,j=2,\ldots ,r\\ -1 & j=i+1, i=2,\ldots ,r \\ 0 & \mr {otherwise} \end{array} \right.$

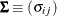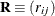Let $\bSigma \equiv (\sigma _{ij})$ and $\bR \equiv (r_{ij})$ be covariance and correlation matrices of 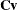$\bC \mb {v}$ , respectively; that is,

$\bSigma = \bC \bV \bC ’$

and

$r_{ij}= \frac{\sigma _{ij}}{\sqrt {\sigma _{ii}\sigma _{jj}}}$

The factor-analytic covariance approximation of Hsu (1992) is to find 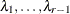$\lambda _1,\ldots ,\lambda _{r-1}$ such that

$\bR = \bD + \blambda \blambda ’$

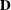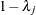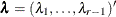where $\bD$ is a diagonal matrix with the jth diagonal element being $1-\lambda _ j$ and $\blambda =(\lambda _1,\ldots ,\lambda _{r-1})’$ . The adjusted p-value is

$p= 1 - \int _{-\infty }^{\infty } \phi (y) \prod _{i=1}^{r-1} \biggl [ \Phi \biggl (\frac{\lambda _ i y + z_{jl}}{\sqrt {1-\lambda _ i^2}}\biggr ) - \Phi \biggl (\frac{\lambda _ i y - z_{jl}}{\sqrt {1-\lambda _ i^2}} \biggr ) \biggr ]dy$

which can be obtained in a DATA step as

$p=\mr {PROBMC}(\mr {"DUNNETT2"}, z_{ij},.,.,r-1,\lambda _1,\ldots ,\lambda _{r-1}).$
Scheffé adjustment:

$p = \mr {Pr}(\chi ^2_{r-1} > z^2_{jl})$
Šidák adjustment:

$p = 1-\{ 1- \mr {Pr}(\chi ^2_1 > z^2_{jl})\} ^ m$
SMM adjustment:

$p = 1 - [2\Phi (z_{jl}) -1]^ m$

which can also be evaluated in a DATA step as

$p = 1 - \mr {PROBMC}(\mr {"MAXMOD"},z_{jl},.,.,m).$
Tukey adjustment:

$p = 1 - \int _{-\infty }^{\infty } r \phi (y)[\Phi (y) - \Phi (y-\sqrt {2}z_{jl})]^{r-1}dy$

which can also be evaluated in a DATA step as

$p = 1 - \mr {PROBMC}(\mr {"RANGE"},\sqrt {2}z_{jl},.,.,r).$

Trend Tests

Trend tests (Klein and Moeschberger, 1997, Section 7.4) have more power to detect ordered alternatives as

$H_2: S_1(t) \ge S_2(t) \ge \ldots \ge S_ k(t), t\le \tau ,$ with at least one inequality

$H_2: S_1(t) \le S_2(t) \le \ldots \le S_ k(t), t\le \tau ,$ with at least one inequality

Let $a_1 < a_2 < \ldots < a_ k$ be a sequence of scores associated with the k samples. The test statistic and its standard error are given by $\sum _{j=1}^ k a_ j v_ j$ and $\sum _{j=1}^ k \sum _{l=1}^ k a_ j a_ l V_{jl}$ , respectively. Under , the z-score

$Z = \frac{ \sum _{j=1}^ k a_ j v_ j}{\sqrt \{ \sum _{j=1}^ k \sum _{l=1}^ k a_ j a_ l V_{jl}\} }$

has, asymptotically, a standard normal distribution. PROC LIFETEST provides both one-tail and two-tail p-values for the test.

Rank Tests for the Association of Survival Time with Covariates

The rank tests for the association of covariates (Kalbfleisch and Prentice, 1980, Chapter 6) are more general cases of the rank tests for homogeneity. In this section, the index $\alpha$ is used to label all observations, $\alpha =1,2,\ldots ,n$ , and the indices range only over the observations that correspond to events, $i,j=1,2,\ldots ,k$ . The ordered event times are denoted as $t_{(i)}$ , the corresponding vectors of covariates are denoted as $\mb {z}_{(i)}$ , and the ordered times, both censored and event times, are denoted as $t_{\alpha }$ .

The rank test statistics have the form

$\mb {v} = \sum _{\alpha =1}^ n c_{\alpha ,\delta _{\alpha }} \mb {z}_{\alpha }$

where n is the total number of observations, $c_{\alpha ,\delta _{\alpha }}$ are rank scores, which can be either log-rank or Wilcoxon rank scores, $\delta _{\alpha }$ is 1 if the observation is an event and 0 if the observation is censored, and $\mb {z}_{\alpha }$ is the vector of covariates in the TEST statement for the $\alpha$ th observation. Notice that the scores, $c_{\alpha ,\delta _{\alpha }}$ , depend on the censoring pattern and that the terms are summed up over all observations.

The log-rank scores are

$c_{\alpha ,\delta _{\alpha }} = \sum _{(j:t_{(j)} \leq t_{\alpha })} \left( \frac{1}{n_ j} - \delta _{\alpha } \right)$

and the Wilcoxon scores are

$c_{\alpha ,\delta _{\alpha }} = 1 - (1 + \delta _{\alpha }) \prod _{(j:t_{(j)} \leq t_{\alpha })} \frac{n_ j}{n_ j + 1}$

where is the number at risk just prior to $t_{(j)}$ .

The estimates used for the covariance matrix of the log-rank statistics are

$\mb {V} = \sum _{i=1}^ k \frac{\mb {V}_ i}{n_ i}$

where $\mb {V}_ i$ is the corrected sum of squares and crossproducts matrix for the risk set at time $t_{(i)}$ ; that is,

$\mb {V}_ i = \sum _{(\alpha :t_{\alpha } \geq t_{(i)} ) } (\mb {z}_{\alpha } - \mb {\bar{z}}_ i)^{\prime } (\mb {z}_{\alpha } - \mb {\bar{z}}_ i)$

where

$\mb {\bar{z}}_ i = \sum _{(\alpha :t_{\alpha } \geq t_{(i)} ) } \frac{\mb {z}_{\alpha }}{n_ i}$

The estimate used for the covariance matrix of the Wilcoxon statistics is

$\mb {V} = \sum _{i=1}^ k \left[ a_ i (1 - a_ i^*) (2\mb {z}_{(i)}\mb {z}_{(i)}^{\prime } + \mb {S}_ i) - (a_ i^* - a_ i) \left( a_ i \mb {x}_ i\mb {x}_ i^{\prime } + \sum _{j=i+1}^ k a_ j (\mb {x}_ i\mb {x}_ j^{\prime } + \mb {x}_ j\mb {x}_ i^{\prime }) \right) \right]$

where

$\displaystyle a_ i$	$\displaystyle =$	$\displaystyle \prod _{j=1}^ i \frac{n_ j}{n_ j + 1}$
$\displaystyle a_ i^*$	$\displaystyle =$	$\displaystyle \prod _{j=1}^ i \frac{n_ j + 1}{n_ j + 2}$
$\displaystyle \Strong{S}_ i$	$\displaystyle =$	$\displaystyle \sum _{(\alpha :t_{(i+1)} > t_{\alpha } > t_{(i)})} \Strong{z}_{\alpha } \Strong{z}_{\alpha }^{\prime }$
$\displaystyle \Strong{x}_ i$	$\displaystyle =$	$\displaystyle 2 \Strong{z}_{(i)} + \sum _{(\alpha :t_{(i+1)} > t_{\alpha } > t_{(i)})} \Strong{z}_{\alpha }$

In the case of tied failure times, the statistics $\mb {v}$ are averaged over the possible orderings of the tied failure times. The covariance matrices are also averaged over the tied failure times. Averaging the covariance matrices over the tied orderings produces functions with appropriate symmetries for the tied observations; however, the actual variances of the $\mb {v}$ statistics would be smaller than the preceding estimates. Unless the proportion of ties is large, it is unlikely that this will be a problem.

The univariate tests for each covariate are formed from each component of $\mb {v}$ and the corresponding diagonal element of $\mb {V}$ as $v_ i^2/V_{ii}$ . These statistics are treated as coming from a chi-square distribution for calculation of probability values.

The statistic $\mb {v^{\prime }V^{-}v}$ is computed by sweeping each pivot of the $\mb {V}$ matrix in the order of greatest increase to the statistic. The corresponding sequence of partial statistics is tabulated. Sequential increments for including a given covariate and the corresponding probabilities are also included in the same table. These probabilities are calculated as the tail probabilities of a chi-square distribution with one degree of freedom. Because of the selection process, these probabilities should not be interpreted as p-values.

If desired for data screening purposes, the output data set requested by the OUTTEST= option can be treated as a sum of squares and crossproducts matrix and processed by the REG procedure by using the option METHOD=RSQUARE. Then the sets of variables of a given size can be found that give the largest test statistics. Product-Limit Estimates and Tests of Association illustrates this process.

The LIFETEST Procedure