Formulas :: SAS/STAT(R) 12.1 User's Guide

Formulas

The following notation is used:

$A_{p}$: intercept for partition p
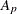
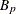
$B_{p}$: slope for partition p
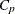
$C_{p}$: power for partition p
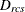
$D_{rcs}$: distance computed from the model between objects r and c for subject s
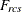
$F_{rcs}$: data weight for objects r and c for subject s obtained from the cth WEIGHT variable, or 1 if there is no WEIGHT statement
f: value of the FIT= option
N: number of objects
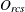
$O_{rcs}$: observed dissimilarity between objects r and c for subject s
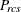
$P_{rcs}$: partition index for objects r and c for subject s
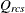
$Q_{rcs}$: dissimilarity after applying any applicable estimated transformation for objects r and c for subject s
$R_{rcs}$: residual for objects r and c for subject s
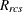
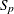
$S_{p}$: standardization factor for partition p
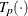
$T_{p}({\cdot })$: estimated transformation for partition p
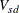
$V_{sd}$: coefficient for subject s on dimension d
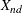
$X_{nd}$: coordinate for object n on dimension d

Summations are taken over nonmissing values.

Distances are computed from the model as

$\begin{tabular}{p{.25in}p{.1in}p{1.5in}p{3in}} $D_{rcs}$ & = & $\sqrt {\displaystyle {\sum _ d(X_{rd}-X_{cd})^2}}$ & {\mbox{for COEF=IDENTITY:} \linebreak Euclidean distance} \\ & = & $\sqrt {\displaystyle {\sum _ d V_{sd}^2(X_{rd}-X_{cd})^2}}$ & {\mbox{for COEF=DIAGONAL:} \linebreak weighted Euclidean distance} \\ \end{tabular}$

Partition indexes are

$\begin{tabular}{p{.3in}p{.1in}p{1.1in}p{1.8in}} $P_{rcs}$ & = & 1 & \mbox{for CONDITION=UN} \\ & = & \Mathtext{s} & \mbox{for CONDITION=MATRIX} \\ & = & $(s-1)N+r$ & \mbox{for CONDITION=ROW} \end{tabular}$

The estimated transformation for each partition is

$\begin{tabular}{p{.3in}p{.1in}p{1.1in}p{1.8in}} $T_ p(d)$ & = & \Mathtext{d} & \mbox{for LEVEL=ABSOLUTE} \\ & = & $B_ pd$ & \mbox{for LEVEL=RATIO} \\ & = & $A_ p+B_ pd$ & \mbox{for LEVEL=INTERVAL} \\ & = & $B_ pd^{C_ p}$ & \mbox{for LEVEL=LOGINTERVAL} \end{tabular}$

For LEVEL=ORDINAL, $T_{p}({\cdot })$ is computed as a least-squares monotone transformation.

For LEVEL=ABSOLUTE, RATIO, or INTERVAL, the residuals are computed as

$\displaystyle Q_{rcs}$	$\displaystyle =$	$\displaystyle O_{rcs}$
$\displaystyle R_{rcs}$	$\displaystyle =$	$\displaystyle Q_{rcs}^ f - [T_{P_{rcs}}(D_{rcs})]^ f$

For LEVEL=ORDINAL, the residuals are computed as

$\displaystyle Q_{rcs}$	$\displaystyle =$	$\displaystyle T_{P_{rcs}}(O_{rcs})$
$\displaystyle R_{rcs}$	$\displaystyle =$	$\displaystyle Q_{rcs}^ f - D_{rcs}^ f$

If f is 0, then natural logarithms are used in place of the fth powers.

For each partition, let

$U_ p = \frac{\displaystyle {\sum _{r,c,s}F_{rcs}}}{\displaystyle {\sum _{r,c,s | P_{rcs}=p}F_{rcs}}}$

and

$\overline{Q}_ p = \frac{\displaystyle {\sum _{r,c,s | P_{rcs}=p}Q_{rcs}F_{rcs}}}{\displaystyle {\sum _{r,c,s | P_{rcs}=p}F_{rcs}}}$

Then the standardization factor for each partition is

$\begin{array}{llll} S_ p & =& 1 & \mbox{for FORMULA=0} \\ & =& U_ p \displaystyle {\sum _{r,c,s | P_{rcs}=p} Q_{rcs}^2F_{rcs} } & \mbox{for FORMULA=1} \\ & =& U_ p \displaystyle {\sum _{r,c,s | P_{rcs}=p} (Q_{rcs}-\overline{Q}_ p)^2F_{rcs} } & \mbox{for FORMULA=2} \end{array}$

The badness-of-fit criterion that the MDS procedure tries to minimize is

$\sqrt {\displaystyle {\sum _{r,c,s} \frac{R_{rcs}^2 F_{rcs} }{S_{P_{rcs}}} } }$

The MDS Procedure

Formulas