The MIXED Procedure

Akaike, H. (1974), “A New Look at the Statistical Model Identification,” IEEE Transaction on Automatic Control, AC-19, 716–723.

Akritas, M. G., Arnold, S. F., and Brunner, E. (1997), “Nonparametric Hypotheses and Rank Statistics for Unbalanced Factorial Designs,” Journal of the American Statistical Association, 92, 258–265.

Allen, D. M. (1974), “The Relationship between Variable Selection and Data Augmentation and a Method of Prediction,” Technometrics, 16, 125–127.

Bates, D. M. and Watts, D. G. (1988), Nonlinear Regression Analysis and Its Applications, John Wiley & Sons.

Beckman, R. J., Nachtsheim, C. J., and Cook, D. R. (1987), “Diagnostics for Mixed-Model Analysis of Variance,” Technometrics, 29, 413–426.

Belsley, D. A., Kuh, E., and Welsch, R. E. (1980), Regression Diagnostics: Identifying Influential Data and Sources of Collinearity, New York: John Wiley & Sons.

Box, G. E. P. and Tiao, G. C. (1973), Bayesian Inference in Statistical Analysis, Wiley Classics Library Edition, published 1992, New York: John Wiley & Sons.

Bozdogan, H. (1987), “Model Selection and Akaike’s Information Criterion (AIC): The General Theory and Its Analytical Extensions,” Psychometrika, 52, 345–370.

Brown, H. and Prescott, R. (1999), Applied Mixed Models in Medicine, New York: John Wiley & Sons.

Brownie, C., Bowman, D. T., and Burton, J. W. (1993), “Estimating Spatial Variation in Analysis of Data from Yield Trials: A Comparison of Methods,” Agronomy Journal, 85, 1244–1253.

Brownie, C. and Gumpertz, M. L. (1997), “Validity of Spatial Analysis of Large Field Trials,” Journal of Agricultural, Biological, and Environmental Statistics, 2, 1–23.

Brunner, E., Dette, H., and Munk, A. (1997), “Box-Type Approximations in Nonparametric Factorial Designs,” Journal of the American Statistical Association, 92, 1494–1502.

Brunner, E., Domhof, S., and Langer, F. (2002), Nonparametric Analysis of Longitudinal Data in Factorial Experiments, New York: John Wiley & Sons.

Burdick, R. K. and Graybill, F. A. (1992), Confidence Intervals on Variance Components, New York: Marcel Dekker.

Burnham, K. P. and Anderson, D. R. (1998), Model Selection and Inference: A Practical Information-Theoretic Approach, New York: Springer-Verlag.

Carlin, B. P. and Louis, T. A. (1996), Bayes and Empirical Bayes Methods for Data Analysis, London: Chapman & Hall.

Carroll, R. J. and Ruppert, D. (1988), Transformation and Weighting in Regression, London: Chapman & Hall.

Chilès, J. P. and Delfiner, P. (1999), Geostatistics-Modeling Spatial Uncertainty, New York: John Wiley & Sons.

Christensen, R., Pearson, L. M., and Johnson, W. (1992), “Case-Deletion Diagnostics for Mixed Models,” Technometrics, 34, 38–45.

Cook, R. D. (1977), “Detection of Influential Observations in Linear Regression,” Technometrics, 19, 15–18.

Cook, R. D. (1979), “Influential Observations in Linear Regression,” Journal of the American Statistical Association, 74, 169–174.

Cook, R. D. and Weisberg, S. (1982), Residuals and Influence in Regression, New York: Chapman & Hall.

Cressie, N. A. C. (1993), Statistics for Spatial Data, New York: John Wiley & Sons.

Crowder, M. J. and Hand, D. J. (1990), Analysis of Repeated Measures, New York: Chapman & Hall.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977), “Maximum Likelihood from Incomplete Data via the EM Algorithm,” Journal of the Royal Statistical Society, Series B, 39, 1–38.

Diggle, P. J. (1988), “An Approach to the Analysis of Repeated Measurements,” Biometrics, 44, 959–971.

Diggle, P. J., Liang, K.-Y., and Zeger, S. L. (1994), Analysis of Longitudinal Data, Oxford: Clarendon Press.

Dunnett, C. W. (1980), “Pairwise Multiple Comparisons in the Unequal Variance Case,” Journal of the American Statistical Association, 75, 796–800.

Edwards, D. and Berry, J. J. (1987), “The Efficiency of Simulation-Based Multiple Comparisons,” Biometrics, 43, 913–928.

Everitt, B. S. (1995), “The Analysis of Repeated Measures: A Practical Review with Examples,” The Statistician, 44, 113–135.

Fai, A. H. T. and Cornelius, P. L. (1996), “Approximate F-Tests of Multiple Degree of Freedom Hypotheses in Generalized Least Squares Analyses of Unbalanced Split-Plot Experiments,” Journal of Statistical Computation and Simulation, 54, 363–378.

Federer, W. T. and Wolfinger, R. D. (1998), “SAS Code for Recovering Intereffect Information in Experiments with Incomplete Block and Lattice Rectangle Designs,” Agronomy Journal, 90, 545–551.

Fuller, W. A. (1976), Introduction to Statistical Time Series, New York: John Wiley & Sons.

Fuller, W. A. and Battese, G. E. (1973), “Transformations for Estimation of Linear Models with Nested Error Structure,” Journal of the American Statistical Association, 68, 626–632.

Galecki, A. T. (1994), “General Class of Covariance Structures for Two or More Repeated Factors in Longitudinal Data Analysis,” Communications in Statistics—Theory and Methods, 23, 3105–3109.

Games, P. A. and Howell, J. F. (1976), “Pairwise Multiple Comparison Procedures with Unequal n’s and/or Variances: A Monte Carlo Study,” Journal of Educational Statistics, 1, 113–125.

Gelfand, A. E., Hills, S. E., Racine-Poon, A., and Smith, A. F. M. (1990), “Illustration of Bayesian Inference in Normal Data Models Using Gibbs Sampling,” Journal of the American Statistical Association, 85, 972–985.

Ghosh, M. (1992), “Discussion of Schervish, M., 'Bayesian Analysis of Linear Models',” in J. M. Bernardo, J. O. Berger, A. P. Dawid, and A. F. M. Smith, eds., Bayesian Statistics 4, 432–433, Oxford: Oxford University Press.

Giesbrecht, F. G. (1989), A General Structure for the Class of Mixed Linear Models, Southern Cooperative Series Bulletin 343, Louisiana Agricultural Experiment Station, Baton Rouge.

Giesbrecht, F. G. and Burns, J. C. (1985), “Two-Stage Analysis Based on a Mixed Model: Large-Sample Asymptotic Theory and Small-Sample Simulation Results,” Biometrics, 41, 477–486.

Golub, G. H. and Van Loan, C. F. (1989), Matrix Computations, Second Edition, Baltimore: Johns Hopkins University Press.

Goodnight, J. H. (1978), Tests of Hypotheses in Fixed-Effects Linear Models, Technical Report R-101, SAS Institute Inc, Cary, NC.

Goodnight, J. H. (1979), “A Tutorial on the Sweep Operator,” The American Statistician, 33, 149–158.

Goodnight, J. H. and Hemmerle, W. J. (1979), “A Simplified Algorithm for the W-Transformation in Variance Component Estimation,” Technometrics, 21, 265–268.

Gotway, C. A. and Stroup, W. W. (1997), “A Generalized Linear Model Approach to Spatial Data and Prediction,” Journal of Agricultural, Biological, and Environmental Statistics, 2, 157–187.

Greenhouse, S. W. and Geisser, S. (1959), “On Methods in the Analysis of Profile Data,” Psychometrika, 32, 95–112.

Gregoire, T. G., Schabenberger, O., and Barrett, J. P. (1995), “Linear Modelling of Irregularly Spaced, Unbalanced, Longitudinal Data from Permanent Plot Measurements,” Canadian Journal of Forest Research, 25, 137–156.

Handcock, M. S. and Stein, M. L. (1993), “A Bayesian Analysis of Kriging,” Technometrics, 35, 403–410.

Handcock, M. S. and Wallis, J. R. (1994), “An Approach to Statistical Spatial-Temporal Modeling of Meteorological Fields (with Discussion),” Journal of the American Statistical Association, 89, 368–390.

Hanks, R. J., Sisson, D. V., Hurst, R. L., and Hubbard, K. G. (1980), “Statistical Analysis of Results from Irrigation Experiments Using the Line-Source Sprinkler System,” Soil Science Society American Journal, 44, 886–888.

Hannan, E. J. and Quinn, B. G. (1979), “The Determination of the Order of an Autoregression,” Journal of the Royal Statistical Society, Series B, 41, 190–195.

Hartley, H. O. and Rao, J. N. K. (1967), “Maximum-Likelihood Estimation for the Mixed Analysis of Variance Model,” Biometrika, 54, 93–108.

Harville, D. A. (1977), “Maximum Likelihood Approaches to Variance Component Estimation and to Related Problems,” Journal of the American Statistical Association, 72, 320–338.

Harville, D. A. (1988), “Mixed-Model Methodology: Theoretical Justifications and Future Directions,” in Proceedings of the Statistical Computing Section, 41–49, New Orleans: American Statistical Association.

Harville, D. A. and Jeske, D. R. (1992), “Mean Squared Error of Estimation or Prediction under a General Linear Model,” Journal of the American Statistical Association, 87, 724–731.

Harville, J. A. (1990), “BLUP (Best Linear Unbiased Prediction), and Beyond,” in Advances in Statistical Methods for Genetic Improvement of Livestock, 239–276, Springer-Verlag.

Hemmerle, W. J. and Hartley, H. O. (1973), “Computing Maximum Likelihood Estimates for the Mixed AOV Model Using the W-Transformation,” Technometrics, 15, 819–831.

Henderson, C. R. (1984), Applications of Linear Models in Animal Breeding, Guelph, ON: University of Guelph.

Henderson, C. R. (1990), “Statistical Method in Animal Improvement: Historical Overview,” in Advances in Statistical Methods for Genetic Improvement of Livestock, 1–14, New York: Springer-Verlag.

Hirotsu, C. and Srivastava, M. (2000), “Simultaneous Confidence Intervals Based on One-Sided Max t Test,” Statistics and Probability Letters, 49, 25–37.

Hsu, J. C. (1992), “The Factor Analytic Approach to Simultaneous Inference in the General Linear Model,” Journal of Computational and Graphical Statistics, 1, 151–168.

Huber, P. J. (1967), “The Behavior of Maximum Likelihood Estimates under Nonstandard Conditions,” Proc. Fifth Berkeley Symp. Math. Statist. Prob., 1, 221–233.

Hurtado, G. I. (1993), Detection of Influential Observations in Linear Mixed Models, Ph.d. dissertation, Department of Statistics, North Carolina State University, 1993.

Hurvich, C. M. and Tsai, C.-L. (1989), “Regression and Time Series Model Selection in Small Samples,” Biometrika, 76, 297–307.

Huynh, H. and Feldt, L. S. (1970), “Conditions Under Which Mean Square Ratios in Repeated Measurements Designs Have Exact F-Distributions,” Journal of the American Statistical Association, 65, 1582–1589.

Jennrich, R. I. and Schluchter, M. D. (1986), “Unbalanced Repeated-Measures Models with Structured Covariance Matrices,” Biometrics, 42, 805–820.

Johnson, D. E., Chaudhuri, U. N., and Kanemasu, E. T. (1983), “Statistical Analysis of Line-Source Sprinkler Irrigation Experiments and Other Nonrandomized Experiments Using Multivariate Methods,” Soil Science Society American Journal, 47, 309–312.

Jones, R. H. and Boadi-Boateng, F. (1991), “Unequally Spaced Longitudinal Data with AR(1) Serial Correlation,” Biometrics, 47, 161–175.

Kackar, R. N. and Harville, D. A. (1984), “Approximations for Standard Errors of Estimators of Fixed and Random Effects in Mixed Linear Models,” Journal of the American Statistical Association, 79, 853–862.

Kass, R. E. and Steffey, D. (1989), “Approximate Bayesian Inference in Conditionally Independent Hierarchical Models (Parametric Empirical Bayes Models),” Journal of the American Statistical Association, 84, 717–726.

Kenward, M. G. (1987), “A Method for Comparing Profiles of Repeated Measurements,” Applied Statistics, 36, 296–308.

Kenward, M. G. and Roger, J. H. (1997), “Small Sample Inference for Fixed Effects from Restricted Maximum Likelihood,” Biometrics, 53, 983–997.

Keselman, H. J., Algina, J., Kowalchuk, R. K., and Wolfinger, R. D. (1998), “A Comparison of Two Approaches for Selecting Covariance Structures in the Analysis of Repeated Measures,” Communications in Statistics—Computation and Simulation, 27, 591–604.

Keselman, H. J., Algina, J., Kowalchuk, R. K., and Wolfinger, R. D. (1999), “A Comparison of Recent Approaches to the Analysis of Repeated Measurements,” British Journal of Mathematical and Statistical Psychology, 52, 63–78.

Kramer, C. Y. (1956), “Extension of Multiple Range Tests to Group Means with Unequal Numbers of Replications,” Biometrics, 12, 307–310.

Laird, N. M., Lange, N., and Stram, D. (1987), “Maximum Likelihood Computations with Repeated Measures: Application of the EM Algorithm,” Journal of the American Statistical Association, 82, 97–105.

Laird, N. M. and Ware, J. H. (1982), “Random-Effects Models for Longitudinal Data,” Biometrics, 38, 963–974.

LaMotte, L. R. (1973), “Quadratic Estimation of Variance Components,” Biometrics, 29, 311–330.

Liang, K.-Y. and Zeger, S. L. (1986), “Longitudinal Data Analysis Using Generalized Linear Models,” Biometrika, 73, 13–22.

Lindsey, J. K. (1993), Models for Repeated Measurements, Oxford: Clarendon Press.

Lindstrom, M. J. and Bates, D. M. (1988), “Newton-Raphson and EM Algorithms for Linear Mixed-Effects Models for Repeated-Measures Data,” Journal of the American Statistical Association, 83, 1014–1022.

Littell, R. C., Milliken, G. A., Stroup, W. W., Wolfinger, R. D., and Schabenberger, O. (2006), SAS for Mixed Models, Second Edition, Cary, NC: SAS Press.

Little, R. J. A. (1995), “Modeling the Drop-Out Mechanism in Repeated-Measures Studies,” Journal of the American Statistical Association, 90, 1112–1121.

Louis, T. A. (1988), “General Methods for Analyzing Repeated Measures,” Statistics in Medicine, 7, 29–45.

Macchiavelli, R. E. and Arnold, S. F. (1994), “Variable Order Ante-dependence Models,” Communications in Statistics—Theory and Methods, 23, 2683–2699.

Marx, D. and Thompson, K. (1987), Practical Aspects of Agricultural Kriging, Bulletin 903, Arkansas Agricultural Experiment Station, Fayetteville, NC.

Matérn, B. (1986), Spatial Variation, Second Edition, New York: Springer-Verlag.

McKeon, J. J. (1974), “F Approximations to the Distribution of Hotelling’s 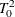,” Biometrika, 61, 381–383.

McLean, R. A. and Sanders, W. L. (1988), “Approximating Degrees of Freedom for Standard Errors in Mixed Linear Models,” Proceedings of the Statistical Computing Section.

McLean, R. A., Sanders, W. L., and Stroup, W. W. (1991), “A Unified Approach to Mixed Linear Models,” The American Statistician, 45, 54–64.

Milliken, G. A. and Johnson, D. E. (1992), Analysis of Messy Data, Volume 1: Designed Experiments, New York: Chapman & Hall.

Moriguchi, S., ed. (1976), Statistical Method for Quality Control, (in Japanese), Tokyo: Japan Standards Association.

Murray, D. M. (1998), Design and Analysis of Group-Randomized Trials, New York: Oxford University Press.

Myers, R. H. (1990), Classical and Modern Regression with Applications, Second Edition, Belmont, CA: PWS-Kent.

Obenchain, R. L. (1990), STABLSIM.EXE, Version 9010, Indianapolis: Eli Lilly, unpublished C code.

Patel, H. I. (1991), “Analysis of Incomplete Data from a Clinical Trial with Repeated Measurements,” Biometrika, 78, 609–619.

Patterson, H. D. and Thompson, R. (1971), “Recovery of Inter-Block Information When Block Sizes Are Unequal,” Biometrika, 58, 545–554.

Pillai, K. C. and Samson, P. (1959), “On Hotelling’s Generalization of 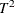,” Biometrika, 46, 160–168.

Pothoff, R. F. and Roy, S. N. (1964), “A Generalized Multivariate Analysis of Variance Model Useful Especially for Growth Curve Problems,” Biometrika, 51, 313–326.

Prasad, N. G. N. and Rao, J. N. K. (1990), “The Estimation of Mean Squared Error of Small-Area Estimators,” Journal of the American Statistical Association, 85, 163–171.

Pringle, R. M. and Rayner, A. A. (1971), Generalized Inverse Matrices with Applications to Statistics, New York: Hafner Publishing.

Rao, C. R. (1972), “Estimation of Variance and Covariance Components in Linear Models,” Journal of the American Statistical Association, 67, 112–115.

Ripley, B. D. (1987), Stochastic Simulation, New York: John Wiley & Sons.

Robinson, G. K. (1991), “That BLUP Is a Good Thing: The Estimation of Random Effects,” Statistical Science, 6, 15–51.

Rubin, D. B. (1976), “Inference and Missing Data,” Biometrika, 63, 581–592.

Sacks, J., Welch, W. J., Mitchell, T. J., and Wynn, H. P. (1989), “Design and Analysis of Computer Experiments,” Statistical Science, 4, 409–435.

Schabenberger, O. and Gotway, C. A. (2005), Statistical Methods for Spatial Data Analysis, Boca Raton, FL: Chapman & Hall/CRC.

Schervish, M. J. (1992), Bayesian Statistics 4, chapter Bayesian Analysis of Linear Models, 419–434, Oxford: Oxford University Press.

Schluchter, M. D. and Elashoff, J. D. (1990), “Small-Sample Adjustments to Tests with Unbalanced Repeated Measures Assuming Several Covariance Structures,” Journal of Statistical Computation and Simulation, 37, 69–87.

Schwarz, G. (1978), “Estimating the Dimension of a Model,” Annals of Statistics, 6, 461–464.

Searle, S. R. (1971), Linear Models, New York: John Wiley & Sons.

Searle, S. R. (1982), Matrix Algebra Useful for Statisticians, New York: John Wiley & Sons.

Searle, S. R. (1988), “Mixed Models and Unbalanced Data: Wherefrom, Whereat, and Whereto?” Communications in Statistics—Theory and Methods, 17, 935–968.

Searle, S. R., Casella, G., and McCulloch, C. E. (1992), Variance Components, New York: John Wiley & Sons.

Self, S. G. and Liang, K.-Y. (1987), “Asymptotic Properties of Maximum Likelihood Estimators and Likelihood Ratio Tests under Nonstandard Conditions,” Journal of the American Statistical Association, 82, 605–610.

Serfling, R. J. (1980), Approximation Theorems of Mathematical Statistics, New York: John Wiley & Sons.

Singer, J. D. (1998), “Using SAS PROC MIXED to Fit Multilevel Models, Hierarchical Models, and Individual Growth Models,” Journal of Educational and Behavioral Statistics, 23, 323–355.

Smith, A. F. M. and Gelfand, A. E. (1992), “Bayesian Statistics without Tears: a Sampling-Resampling Perspective,” The American Statistician, 46, 84–88.

Snedecor, G. W. and Cochran, W. G. (1976), Statistical Methods, Sixth Edition, Ames: Iowa State University Press.

Snedecor, G. W. and Cochran, W. G. (1980), Statistical Methods, Seventh Edition, Ames: Iowa State University Press.

Steel, R. G. D., Torrie, J. H., and Dickey, D. (1997), Principles and Procedures of Statistics: A Biometrical Approach, Third Edition, New York: McGraw-Hill.

Stram, D. O. and Lee, J. W. (1994), “Variance Components Testing in the Longitudinal Mixed Effects Model,” Biometrics, 50, 1171–1177.

Stroup, W. W. (1989a), Predictable Functions and Prediction Space in the Mixed Model Procedure, Southern Cooperative Series Bulletin 343, Louisiana Agricultural Experiment Station, Baton Rouge, LA.

Stroup, W. W. (1989b), “Use of Mixed Model Procedure to Analyze Spatially Correlated Data: An Example Applied to a Line-Source Sprinkler Irrigation Experiment,” Applications of Mixed Models in Agriculture and Related Disciplines.

Stroup, W. W., Baenziger, P. S., and Mulitze, D. K. (1994), “Removing Spatial Variation from Wheat Yield Trials: A Comparison of Methods,” Crop Science, 86, 62–66.

Sullivan, L. M., Dukes, K. A., and Losina, E. (1999), “An Introduction to Hierarchical Linear Modelling,” Statistics in Medicine, 18, 855–888.

Swallow, W. H. and Monahan, J. F. (1984), “Monte Carlo Comparison of ANOVA, MIVQUE, REML, and ML Estimators of Variance Components,” Technometrics, 28, 47–57.

Tamhane, A. C. (1979), “A Comparison of Procedures for Multiple Comparisons of Means with Unequal Variances,” Journal of the American Statistical Association, 74, 471–480.

Tierney, L. (1994), “Markov Chains for Exploring Posterior Distributions,” Annals of Statistics, 22(4), 1701–1762.

Verbeke, G. and Molenberghs, G., eds. (1997), Linear Mixed Models in Practice: A SAS-Oriented Approach, New York: Springer.

Verbeke, G. and Molenberghs, G. (2000), Linear Mixed Models for Longitudinal Data, New York: Springer.

Westfall, P. H., Tobias, R. D., Rom, D., Wolfinger, R. D., and Hochberg, Y. (1999), Multiple Comparisons and Multiple Tests Using the SAS System, Cary, NC: SAS Institute Inc.

Westfall, P. J. and Young, S. S. (1993), Resampling-Based Multiple Testing, New York: John Wiley & Sons.

White, H. (1980), “A Heteroskedasticity-Consistent Covariance Matrix Estimator and a Direct Test for Heteroskedasticity,” Econometrica, 48, 817–838.

Whittle, P. (1954), “On Stationary Processes in the Plane,” Biometrika, 41, 434–449.

Winer, B. J. (1971), Statistical Principles in Experimental Design, Second Edition, New York: McGraw-Hill.

Wolfinger, R. D. (1993), “Covariance Structure Selection in General Mixed Models,” Communications in Statistics, Simulation, and Computation, 22(4), 1079–1106.

Wolfinger, R. D. (1996), “Heterogeneous Variance-Covariance Structures for Repeated Measures,” Journal of Agricultural, Biological, and Environmental Statistics, 1, 205–230.

Wolfinger, R. D. (1997), “An Example of Using Mixed Models and PROC MIXED for Longitudinal Data,” Journal of Biopharmaceutical Statistics, 7(4), 481–500.

Wolfinger, R. D. and Chang, M. (1995), “Comparing the SAS GLM and MIXED Procedures for Repeated Measures,” in Proceedings of the Twentieth Annual SAS Users Group Conference, Cary, NC: SAS Institute Inc.

Wolfinger, R. D., Tobias, R. D., and Sall, J. (1991), “Mixed Models: A Future Direction,” in Proceedings of the Sixteenth Annual SAS Users Group Conference, Cary, NC: SAS Institute Inc.

Wolfinger, R. D., Tobias, R. D., and Sall, J. (1994), “Computing Gaussian Likelihoods and Their Derivatives for General Linear Mixed Models,” SIAM Journal on Scientific Computing, 15, 1294–1310.

Wright, P. S. (1994), Adjusted F Tests for Repeated Measures with the MIXED Procedure, 328 SMC-Statistics Department, University of Tennessee.

Zimmerman, D. L. and Harville, D. A. (1991), “A Random Field Approach to the Analysis of Field-Plot Experiments and Other Spatial Experiments,” Biometrics, 47, 223–239.