The PROBIT Procedure

Example 75.5 Model Postfitting Analysis

Recall the previous example of an epidemic study, in which the treat*sex interaction is statistically significant. Suppose you want to know whether such an effect is the same at different levels of the two categorical variables.

The following SAS statements fit a probit model and use the SLICE statement to request analysis of the two-way interaction term treat*sex:

proc probit data=epidemic;
   class treat sex;
   model r/n = dose treat sex treat*sex;
   slice treat*sex / diff;
   effectplot;
run;

Output 75.5.1 displays the test results for the interaction effect. As you can see, the difference between the two treatments is not significant among females.

Output 75.5.1: Tests Conditional on treat*sex

The Probit Procedure

Chi-Square Test for treat*sex Least Squares Means Slice
Slice	Num DF	Chi-Square	Pr > ChiSq
treat A	1	18.52	<.0001

Chi-Square Test for treat*sex Least Squares Means Slice
Slice	Num DF	Chi-Square	Pr > ChiSq
treat B	1	2.65	0.1035

Chi-Square Test for treat*sex Least Squares Means Slice
Slice	Num DF	Chi-Square	Pr > ChiSq
sex 0	1	0.00	0.9579

Chi-Square Test for treat*sex Least Squares Means Slice
Slice	Num DF	Chi-Square	Pr > ChiSq
sex 1	1	47.43	<.0001

The DIFF option computes effect differences between groups within the same slice. Results are displayed in Output 75.5.2.

Output 75.5.2: Effect Differences Conditional on treat*sex

Simple Differences of treat*sex Least Squares Means
Slice	sex	_sex	Estimate	Standard Error	z Value	Pr > \|z\|
treat A	0	1	0.5957	0.1384	4.30	<.0001

Simple Differences of treat*sex Least Squares Means
Slice	sex	_sex	Estimate	Standard Error	z Value	Pr > \|z\|
treat B	0	1	-0.2956	0.1816	-1.63	0.1035

Simple Differences of treat*sex Least Squares Means
Slice	treat	_treat	Estimate	Standard Error	z Value	Pr > \|z\|
sex 0	A	B	-0.00899	0.1702	-0.05	0.9579

Simple Differences of treat*sex Least Squares Means
Slice	treat	_treat	Estimate	Standard Error	z Value	Pr > \|z\|
sex 1	A	B	-0.9003	0.1307	-6.89	<.0001

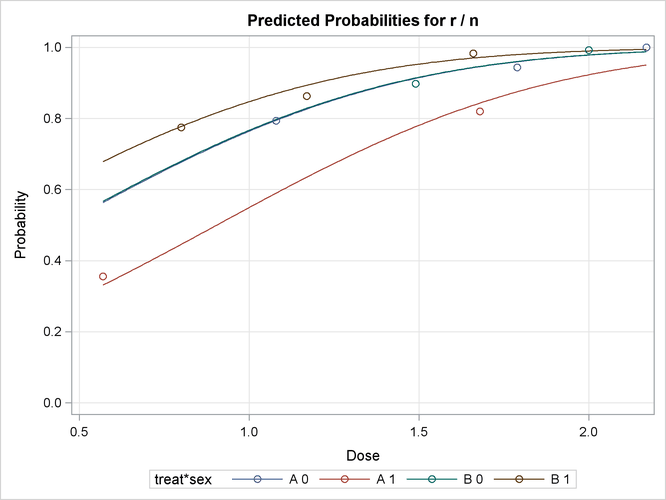
The EFFECTPLOT statement produces a predicted probability plot for dose by the four groups that are formed by the treat*sex interaction. The plot is displayed in Output 75.5.3. The two overlapping curves represent the two treatment groups for females, suggesting no treatment effect. It appears that males tend to respond to the two treatments differently: those on treatment B have a better survival rate, and those on treatment A have a worse chance of survival.

Output 75.5.3: Predicted Probability versus Dose Level by treat*sex