The QUANTREG Procedure

Linear Test

Testing Effects of Covariates
Testing for Heteroscedasticity

Consider the linear model

$y_ i =\mb {x}_{1i}^{\prime }\bbeta _1 + \mb {x}_{2i}^{\prime }\bbeta _2 + \epsilon _ i$

where $\bbeta _1$ and $\bbeta _2$ are and dimensional unknown parameters, and $\{ \epsilon _ i\}$ , $i=1,\ldots ,n$ , are errors with unknown density function . Let $\mb {x}_ i^{\prime }=(\mb {x}_{1i}^{\prime }, \mb {x}_{2i}^{\prime })$ ; $\hat\bbeta _1(\tau )$ and $\hat\bbeta _2(\tau )$ be the parameter estimates for $\bbeta _1$ and $\bbeta _2$ respectively at the $\tau$ quantile. The covariance matrix $\bOmega$ for the parameter estimates is partitioned correspondingly as $\bOmega _{ij}$ with ; and $\bOmega ^{22} = (\bOmega _{22} - \bOmega _{21} \bOmega _{11}^{-1} \bOmega _{12})^{-1}.$

Testing Effects of Covariates

Three tests are available in the QUANTREG procedure for the linear null hypothesis $H_{0}: \beta _2 = 0$ at the $\tau$ quantile.

The Wald test statistic, which is based on the estimated coefficients for the unrestricted model, is given by

$T_ W(\tau ) = {\hat\bbeta _2^{\prime }(\tau )} {\hat\bSigma (\tau )}^{-1} {\hat\bbeta _2(\tau )}$

where ${\hat\bSigma (\tau )}$ is an estimator of the covariance of ${\hat\bbeta _2(\tau )}$ . The QUANTREG procedure provides two estimators for the covariance, as described in the previous section. The estimator based on the asymptotic covariance is

${\hat\bSigma (\tau )} = {\frac1n} {\hat\omega (\tau )}^{2} {\bOmega }^{22}$

where ${\hat\omega (\tau )} = \sqrt {\tau (1-\tau )}{\hat s(\tau )}$ and ${\hat s(\tau )}$ is the estimated sparsity function. The estimator based on the bootstrap covariance is the empirical covariance of the MCMB samples.

The likelihood ratio test is based on the difference between the objective function values in the restricted and unrestricted models. Let $D_0(\tau )=\sum \rho _\tau (y_ i-\mb {x}_ i{\hat\bbeta }(\tau ))$ and $D_1(\tau )=\sum \rho _\tau (y_ i-\mb {x}_{1i}{\hat\bbeta _1}(\tau ))$ , and set

$T_{\mr {LR}}(\tau ) = 2 ({\tau (1-\tau )}{\hat s(\tau )})^{-1} ( D_1(\tau ) - D_0(\tau ) )$

where ${\hat s(\tau )}$ is the estimated sparsity function.

The rank test statistic is given by

$T_ R(\tau ) = \bS _ n^{\prime } \bM _ n^{-1} \bS _ n/A^2(\varphi )$

where

$\bS _ n=n^{-1/2} (\bX _2 - \hat{\bX }_2)^{\prime } \hat{\mb {b}}_ n$

$\bPsi =\mr {diag}(f_ i(Q_{y_ i}(\tau |\mb {x}_{1i},\mb {x}_{2i})))$

$\hat{\bX }_2 = \bX _1(\bX _1^{\prime } \bPsi {\bX _1})^{-1}\bX _1^{\prime } {\bX _2}$

$\bM _ n = (\bX _2 - \hat{\bX }_2) (\bX _2 - \hat{\bX }_2)^{\prime }/n$

$\hat{\mb {b}}_{ni} = \int _0^1 \hat{\mb {a}}_{ni}(t) d \varphi (t)$

$\hat{\mb {a}}(t) = \max _ a \{ \mb {y}^{\prime }\mb {a} | \bX _1^{\prime }\mb {a} = (1-t)\bX _1^{\prime }\mb {e}, \ \mb {a}\in [0,1]^ n \}$

$A^2(\varphi ) = \int _0^1 (\varphi (t) - \bar{\varphi }(t))^2 dt$

$\bar{\varphi }(t) = \int _0^1 \varphi (t) dt$

and $\varphi (t)$ is a score function.

The following score functions are available in the QUANTREG procedure:

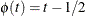
Wilcoxon scores:: $\phi (t) = t - {1\slash 2}$
Normal scores: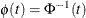: $\phi (t) = \Phi ^{-1}(t)$ , where 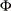$\Phi$ is the normal distribution function
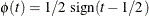
Sign scores:: $\phi (t) ={1\slash 2} {\mbox{ sign}}(t-{1\slash 2})$
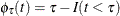Tau scores:: $\phi _\tau (t) = \tau - I{(t<\tau )}$ .

The rank test statistic $T_ R(\tau )$ , unlike Wald tests or likelihood ratio tests, requires no estimation of the nuisance parameter under iid error models (Gutenbrunner et al., 1993).

Koenker and Machado (1999) prove that the three test statistics ( $T_ W(\tau ), T_{\mr {LR}}(\tau )$ , and $T_ R(\tau )$ ) are asymptotically equivalent and that their distributions converge to $\chi _ q^2$ under the null hypothesis, where q is the dimension of $\beta _2$ .

Testing for Heteroscedasticity

After you obtain the parameter estimates for several quantiles specified in the MODEL statement, you can test whether there are significant difference for the estimates for the same covariates across the quantiles. For example, if you want to test whether the parameters $\beta _2$ are the same across quantiles, the null hypothesis $H_{0}$ can be written as: $\beta _2(\tau _1) = ... = \beta _2(\tau _ k)$ , where $\tau _ j, j=1, ..., k,$ are the quantiles specified in the MODEL statement. See Koenker and Bassett (1982a) for details.