The SEQTEST Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Input Data SetsBoundary VariablesInformation Level Adjustments at Future StagesBoundary Adjustments for Information LevelsBoundary Adjustments for Minimum Error SpendingBoundary Adjustments for Overlapping Lower and Upper beta BoundariesStochastic CurtailmentRepeated Confidence IntervalsAnalysis after a Sequential TestAvailable Sample Space Orderings in a Sequential TestApplicable Tests and Sample Size ComputationTable OutputODS Table NamesGraphics OutputODS Graphics
Input Data SetsBoundary VariablesInformation Level Adjustments at Future StagesBoundary Adjustments for Information LevelsBoundary Adjustments for Minimum Error SpendingBoundary Adjustments for Overlapping Lower and Upper beta BoundariesStochastic CurtailmentRepeated Confidence IntervalsAnalysis after a Sequential TestAvailable Sample Space Orderings in a Sequential TestApplicable Tests and Sample Size ComputationTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Testing the Difference between Two ProportionsTesting an Effect in a Regression ModelTesting an Effect with Early Stopping to Accept H0Testing a Binomial ProportionComparing Two Proportions with a Log Odds Ratio TestComparing Two Survival Distributions with a Log-Rank TestTesting an Effect in a Proportional Hazards Regression ModelTesting an Effect in a Logistic Regression ModelConducting a Trial with a Nonbinding Acceptance Boundary
Testing the Difference between Two ProportionsTesting an Effect in a Regression ModelTesting an Effect with Early Stopping to Accept H0Testing a Binomial ProportionComparing Two Proportions with a Log Odds Ratio TestComparing Two Survival Distributions with a Log-Rank TestTesting an Effect in a Proportional Hazards Regression ModelTesting an Effect in a Logistic Regression ModelConducting a Trial with a Nonbinding Acceptance Boundary - References
Example 84.1 Testing the Difference between Two Proportions
This example demonstrates group sequential tests that use an O’Brien-Fleming group sequential design. A clinic is studying the effect of vitamin C supplements in treating flu symptoms. The study consists of patients in the clinic who have exhibited the first sign of flu symptoms within the last 24 hours. These patients are randomly assigned to either the control group (which receives placebo pills) or the treatment group (which receives large doses of vitamin C supplements). At the end of a five-day period, the flu symptoms of each patient are recorded.
Suppose that you know from past experience that flu symptoms disappear in five days for 60% of patients who experience flu
symptoms. The clinic would like to detect a 75% symptom disappearance with a high probability. A test that compares the proportions
directly specifies the null hypothesis ![]() with a one-sided alternative
with a one-sided alternative ![]() and a power of 0.90 at
and a power of 0.90 at ![]() , where
, where ![]() and
and ![]() are the proportions of symptom disappearance in the treatment group and control group, respectively.
are the proportions of symptom disappearance in the treatment group and control group, respectively.
The following statements invoke the SEQDESIGN procedure and request a four-stage group sequential design by using an O’Brien-Fleming
method for normally distributed data. The design uses a one-sided alternative hypothesis with early stopping either to accept
or reject the null hypothesis ![]() . The BOUNDARYSCALE=MLE option uses the MLE scale to display statistics in the boundary table and boundary plots.
. The BOUNDARYSCALE=MLE option uses the MLE scale to display statistics in the boundary table and boundary plots.
ods graphics on;
proc seqdesign altref=0.15
boundaryscale=mle
;
OBrienFleming: design method=obf
nstages=4
alt=upper
stop=both
alpha=0.025
;
samplesize model=twosamplefreq(nullprop=0.6 test=prop);
ods output Boundary=Bnd_Count;
run;
ods graphics off;
The ODS OUTPUT statement with the BOUNDARY=BND_COUNT option creates an output data set named BND_COUNT which contains the resulting boundary information for the subsequent sequential tests.
The “Design Information” table in Output 84.1.1 displays design specifications. With the specified alternative hypothesis ![]() , the maximum information is derived to achieve a power of 0.90 at
, the maximum information is derived to achieve a power of 0.90 at ![]() . The derived fixed-sample information ratio 1.0767 is the maximum information needed for a group sequential design relative
to its corresponding fixed-sample design.
. The derived fixed-sample information ratio 1.0767 is the maximum information needed for a group sequential design relative
to its corresponding fixed-sample design.
Output 84.1.1: O’Brien-Fleming Design Information
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | MLE |
| Alternative Hypothesis | Upper |
| Early Stop | Accept/Reject Null |
| Method | O'Brien-Fleming |
| Boundary Key | Both |
| Alternative Reference | 0.15 |
| Number of Stages | 4 |
| Alpha | 0.025 |
| Beta | 0.1 |
| Power | 0.9 |
| Max Information (Percent of Fixed Sample) | 107.6741 |
| Max Information | 502.8343 |
| Null Ref ASN (Percent of Fixed Sample) | 61.12891 |
| Alt Ref ASN (Percent of Fixed Sample) | 75.89782 |
The “Boundary Information” table in Output 84.1.2 displays the information level, alternative reference, and boundary values at each stage. With the BOUNDARYSCALE=MLE option, the SEQDESIGN procedure displays the output boundaries with the maximum likelihood estimator scale.
Output 84.1.2: O’Brien-Fleming Boundary Information
| Boundary Information (MLE Scale) Null Reference = 0 |
||||||
|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | ||||
| Information Level | Reference | Upper | ||||
| Proportion | Actual | N | Upper | Beta | Alpha | |
| 1 | 0.2500 | 125.7086 | 107.4808 | 0.15000 | -0.09709 | 0.35291 |
| 2 | 0.5000 | 251.4171 | 214.9617 | 0.15000 | 0.02645 | 0.17645 |
| 3 | 0.7500 | 377.1257 | 322.4425 | 0.15000 | 0.06764 | 0.11764 |
| 4 | 1.0000 | 502.8343 | 429.9233 | 0.15000 | 0.08823 | 0.08823 |
With ODS Graphics enabled, a detailed boundary plot with the rejection and acceptance regions is displayed, as shown in Output 84.1.3. The horizontal axis indicates the information levels for the design. The stages are indicated by vertical lines with accompanying stage numbers. If the test statistic at a stage is in a rejection region, the trial stops and the hypothesis is rejected. If the test statistic is in an acceptance region, then the trial also stops and the hypothesis is accepted. If the statistic is not in a rejection or an acceptance region, the trial continues to the next stage.
Output 84.1.3: O’Brien-Fleming Boundary Plot
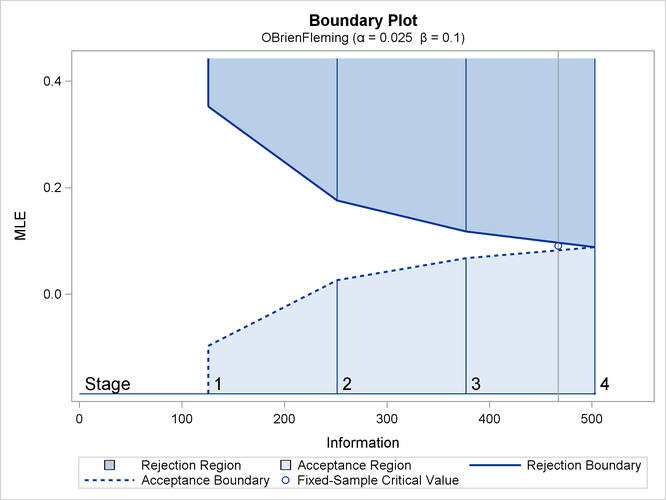
The boundary plot also displays the information level and critical value for the corresponding fixed-sample design. The solid and dashed lines at the fixed-sample information level correspond to the rejection and acceptance lines, respectively.
With the SAMPLESIZE statement, the maximum information is used to derive the required sample size for the study. The “Sample Size Summary” table in Output 84.1.4 displays parameters for the sample size computation.
Output 84.1.4: Required Sample Size Summary
| Sample Size Summary | |
|---|---|
| Test | Two-Sample Proportions |
| Null Proportion | 0.6 |
| Proportion (Group A) | 0.75 |
| Test Statistic | Z for Proportion |
| Reference Proportions | Alt Ref |
| Max Sample Size | 429.9233 |
| Expected Sample Size (Null Ref) | 244.0768 |
| Expected Sample Size (Alt Ref) | 303.0464 |
With the derived maximum information and the specified MODEL= option in the SAMPLESIZE statement, the total sample size in each group for testing the difference between two proportions under the alternative hypothesis is
|
|
where ![]() and
and ![]() . By default (or equivalently if you specify REF=PROP in the MODEL=TWOSAMPLEFREQ option), the required sample sizes are computed
under the alternative hypothesis. See the section “Test for the Difference between Two Binomial Proportions” in the chapter “The SEQDESIGN Procedure” for a description of these parameters.
. By default (or equivalently if you specify REF=PROP in the MODEL=TWOSAMPLEFREQ option), the required sample sizes are computed
under the alternative hypothesis. See the section “Test for the Difference between Two Binomial Proportions” in the chapter “The SEQDESIGN Procedure” for a description of these parameters.
The “Sample Sizes (N)” table in Output 84.1.5 displays the required sample sizes at each stage, in both fractional and integer numbers. The derived sample sizes under
the heading Fractional N which correspond to the design are not integers. These sample sizes are rounded up to integers under the heading Ceiling N. In practice, integer sample sizes are used, and the information levels increase slightly. Thus, 54, 108, 162, and 215 patients
are needed in each group for the four stages, respectively.
Output 84.1.5: Required Sample Sizes
| Sample Sizes (N) Two-Sample Z Test for Proportion Difference |
||||||||
|---|---|---|---|---|---|---|---|---|
| _Stage_ | Fractional N | Ceiling N | ||||||
| N | N(Grp 1) | N(Grp 2) | Information | N | N(Grp 1) | N(Grp 2) | Information | |
| 1 | 107.48 | 53.74 | 53.74 | 125.7 | 108 | 54 | 54 | 126.3 |
| 2 | 214.96 | 107.48 | 107.48 | 251.4 | 216 | 108 | 108 | 252.6 |
| 3 | 322.44 | 161.22 | 161.22 | 377.1 | 324 | 162 | 162 | 378.9 |
| 4 | 429.92 | 214.96 | 214.96 | 502.8 | 430 | 215 | 215 | 502.9 |
Suppose the trial follows the study plan, and 54 patients are available in each group at stage 1. The data set count_1 contains these 108 patients. Output 84.1.6 lists the first 10 observations of the data set.
Output 84.1.6: Clinical Trial Data
| First 10 Obs in the Trial Data |
| Obs | Trt | Resp |
|---|---|---|
| 1 | 0 | 0 |
| 2 | 1 | 1 |
| 3 | 0 | 1 |
| 4 | 1 | 0 |
| 5 | 0 | 0 |
| 6 | 1 | 0 |
| 7 | 0 | 0 |
| 8 | 1 | 1 |
| 9 | 0 | 1 |
| 10 | 1 | 0 |
The Trt variable is a grouping variable with value 0 for a patient in the placebo control group and value 1 for a patient in the
treatment group who is given vitamin C supplements. The Resp variable is an indicator variable with value 1 for a patient without flu symptoms after five days and value 0 for a patient
with flu symptoms after five days.
The following statements use the GENMOD procedure to estimate the treatment effect at stage 1:
proc genmod data=count_1; model Resp= Trt; ods output ParameterEstimates=Parms_Count1; run;
Output 84.1.7 displays the treatment effect at stage 1.
Output 84.1.7: Stage 1 Treatment Difference
| Analysis Of Maximum Likelihood Parameter Estimates | |||||||
|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | Wald 95% Confidence Limits | Wald Chi-Square | Pr > ChiSq | |
| Intercept | 1 | 0.6296 | 0.0627 | 0.5066 | 0.7526 | 100.68 | <.0001 |
| Trt | 1 | 0.1111 | 0.0887 | -0.0628 | 0.2850 | 1.57 | 0.2105 |
| Scale | 1 | 0.4611 | 0.0314 | 0.4035 | 0.5269 | ||
| Note: | The scale parameter was estimated by maximum likelihood. |
The test statistic is ![]() , and its associated standard error is
, and its associated standard error is
|
|
The following statements create and display (in Output 84.1.8) the data set that contains the parameter estimate at stage 1, ![]() , and its associated standard error
, and its associated standard error ![]() which are used in the SEQTEST procedure:
which are used in the SEQTEST procedure:
data Parms_Count1; set Parms_Count1; if Parameter='Trt'; _Scale_='MLE'; _Stage_= 1; keep _Scale_ _Stage_ Parameter Estimate StdErr; run; proc print data=Parms_Count1; title 'Statistics Computed at Stage 1'; run;
Output 84.1.8: Statistics Computed at Stage 1
| Statistics Computed at Stage 1 |
| Obs | Parameter | Estimate | StdErr | _Scale_ | _Stage_ |
|---|---|---|---|---|---|
| 1 | Trt | 0.1111 | 0.0887 | MLE | 1 |
The initial required sample sizes are derived with the proportions ![]() and
and ![]() . If the observed proportions are different from these assumed values, or if the number of available patients is different
from the study plan in one of the stages, then the information level that corresponds to the test statistic is estimated from
. If the observed proportions are different from these assumed values, or if the number of available patients is different
from the study plan in one of the stages, then the information level that corresponds to the test statistic is estimated from
|
|
The following statements invoke the SEQTEST procedure and test for early stopping at stage 1:
ods graphics on;
proc seqtest Boundary=Bnd_Count
Parms(Testvar=Trt)=Parms_Count1
infoadj=none
errspendmin=0.001
boundaryscale=mle
errspend
plots=errspend
;
ods output Test=Test_Count1;
run;
ods graphics off;
The BOUNDARY= option specifies the input data set that provides the boundary information for the trial at stage 1, which was
generated in the SEQDESIGN procedure. The PARMS=PARMS_COUNT1 option specifies the input data set PARMS_COUNT1 that contains the test statistic and its associated standard error at stage 1, and the TESTVAR=TRT option identifies the
test variable TRT in the data set. The INFOADJ=NONE option maintains the information levels at future interim stages (2 and 3) as provided
in the BOUNDARY= data set. The BOUNDARYSCALE=MLE option displays the output boundaries in terms of the MLE scale.
The O’Brien-Fleming design is conservative in early stages and might not be desirable in a clinical trial. The ERRSPENDMIN=0.001 option specifies the minimum error spending at each stage to be 0.001, and it might increase the corresponding nominal p-value in early stages for the trial. The BOUNDARYSCALE=MLE option uses the MLE scale to display test statistics in the boundary table and boundary plots.
The ODS OUTPUT statement with the TEST=TEST_COUNT1 option creates an output data set named TEST_COUNT1 which contains the updated boundary information for the test at stage 1. The data set also provides the boundary information
that is needed for the group sequential test at the next stage.
The “Design Information” table in Output 84.1.9 displays design specifications. The derived statistics, such as the overall ![]() and
and ![]() levels, are derived from the specified maximum information and boundary values in the BOUNDARY= data set. Note that with
a minor change in the information level at stage 1, the power also changes slightly from the design provided in the BOUNDARY=
data set.
levels, are derived from the specified maximum information and boundary values in the BOUNDARY= data set. Note that with
a minor change in the information level at stage 1, the power also changes slightly from the design provided in the BOUNDARY=
data set.
Output 84.1.9: Design Information
| Design Information | |
|---|---|
| BOUNDARY Data Set | WORK.BND_COUNT |
| Data Set | WORK.PARMS_COUNT1 |
| Statistic Distribution | Normal |
| Boundary Scale | MLE |
| Alternative Hypothesis | Upper |
| Early Stop | Accept/Reject Null |
| Number of Stages | 4 |
| Alpha | 0.025 |
| Beta | 0.10147 |
| Power | 0.89853 |
| Max Information (Percent of Fixed Sample) | 108.2301 |
| Max Information | 502.834283 |
| Null Ref ASN (Percent of Fixed Sample) | 61.09917 |
| Alt Ref ASN (Percent of Fixed Sample) | 73.9745 |
With the ERRSPEND option, the “Error Spending Information” table in Output 84.1.10 displays cumulative error spending at each stage for each boundary. By default (or equivalently if you specify BOUNDARYKEY=ALPHA),
the Type I error level ![]() is maintained. Furthermore, with the ERRSPENDMIN=0.001 option, the
is maintained. Furthermore, with the ERRSPENDMIN=0.001 option, the ![]() spending at each stage is greater than or equal to 0.001.
spending at each stage is greater than or equal to 0.001.
Output 84.1.10: Error Spending Information
| Error Spending Information | ||||
|---|---|---|---|---|
| _Stage_ | Cumulative Error Spending | |||
| Information Level | Upper | |||
| Proportion | Actual | Beta | Alpha | |
| 1 | 0.2525 | 126.9871 | 0.00308 | 0.00100 |
| 2 | 0.5000 | 251.4171 | 0.02653 | 0.00343 |
| 3 | 0.7500 | 377.1257 | 0.06456 | 0.01254 |
| 4 | 1.0000 | 502.8343 | 0.10147 | 0.02500 |
With the PLOTS=ERRSPEND option, the procedure displays a plot of error spending for each boundary, as shown in Output 84.1.11. The error spending values in the “Error Spending Information” table in Output 84.1.10 are displayed in the plot.
Output 84.1.11: Error Spending Plot
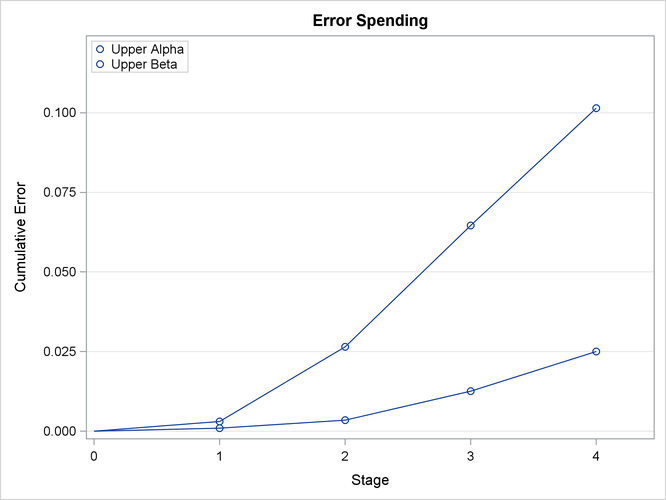
The “Test Information” table in Output 84.1.12 displays the boundary values for the design, test statistic, and resulting action at each stage. With the BOUNDARYSCALE=MLE
option, the maximum likelihood estimator scale is used for the test statistic and boundary values. The table shows that the
test statistic 0.1111 is between the upper ![]() and
and ![]() boundaries, so the trial continues to the next stage.
boundaries, so the trial continues to the next stage.
Output 84.1.12: Sequential Test
| Test Information (MLE Scale) Null Reference = 0 |
|||||||
|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | Test | ||||
| Information Level | Reference | Upper | Trt | ||||
| Proportion | Actual | Upper | Beta | Alpha | Estimate | Action | |
| 1 | 0.2525 | 126.9871 | 0.15000 | -0.09306 | 0.27423 | 0.11111 | Continue |
| 2 | 0.5000 | 251.4171 | 0.15000 | 0.02674 | 0.17527 | . | |
| 3 | 0.7500 | 377.1257 | 0.15000 | 0.06805 | 0.11792 | . | |
| 4 | 1.0000 | 502.8343 | 0.15000 | 0.08875 | 0.08875 | . | |
The information level at stage 1 is derived from the standard error,
|
|
By default (or equivalently if you specify PLOTS=TEST), the “Test Plot” graph displays boundary values of the design and the test statistic at stage 1, as shown in Output 84.1.13. It also shows that the observed statistic is in the continuation region.
Output 84.1.13: Sequential Test Plot
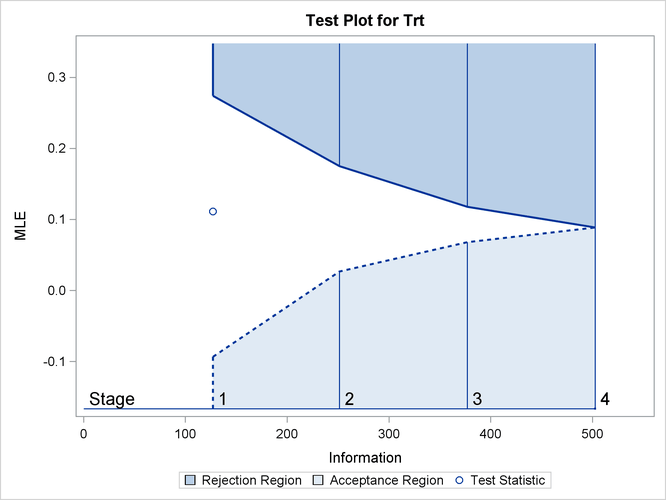
The observed information level at stage 1, ![]() , is slightly larger than the target information level at the design. If an observed information level in the study is substantially
different from its target level in the design, then the sample sizes should be adjusted in the subsequent stages to achieve
the target information levels.
, is slightly larger than the target information level at the design. If an observed information level in the study is substantially
different from its target level in the design, then the sample sizes should be adjusted in the subsequent stages to achieve
the target information levels.
Suppose the trial continues to the next stage, and 108 patients are available in each group at stage 2. The data set COUNT_2 contains these 216 patients.
The following statements use the GENMOD procedure to estimate the treatment effect at stage 2:
proc genmod data=Count_2; model Resp= Trt; ods output ParameterEstimates=Parms_Count2; run;
The following statements create the parameter estimate at stage 2, ![]() , and its associated standard error
, and its associated standard error ![]() into a test data set:
into a test data set:
data Parms_Count2; set Parms_Count2; if Parameter='Trt'; _Scale_='MLE'; _Stage_= 2; keep _Scale_ _Stage_ Parameter Estimate StdErr; run; proc print data=Parms_Count2; title 'Statistics Computed at Stage 2'; run;
Output 84.1.14 displays the test statistics at stage 2.
Output 84.1.14: Statistics Computed at Stage 2
| Statistics Computed at Stage 2 |
| Obs | Parameter | Estimate | StdErr | _Scale_ | _Stage_ |
|---|---|---|---|---|---|
| 1 | Trt | 0.1759 | 0.0623 | MLE | 2 |
The following statements invoke the SEQTEST procedure and test for early stopping at stage 2:
ods graphics on;
proc seqtest Boundary=Test_Count1
Parms(Testvar=Trt)=Parms_Count2
infoadj=none
boundaryscale=mle
;
ods output Test=Test_Count2;
run;
ods graphics off;
The BOUNDARY= option specifies the input data set that provides the boundary information for the trial at stage 2, which was generated by the SEQTEST procedure at the previous stage. The PARMS= option specifies the input data set that contains the test statistic and its associated standard error at stage 2, and the TESTVAR= option identifies the test variable in the data set.
The ODS OUTPUT statement with the TEST=TEST_COUNT2 option creates an output data set named TEST_COUNT2 which contains the updated boundary information for the test at stage 2. The data set also provides the boundary information
that is needed for the group sequential test at the next stage.
The “Test Information” table in Output 84.1.15 displays the boundary values, test statistic, and resulting action at each stage. The table shows that the test statistic 0.17593 is larger than the corresponding upper alpha boundary value, so the trial stops to reject the hypothesis.
Output 84.1.15: Sequential Test
| Test Information (MLE Scale) Null Reference = 0 |
|||||||
|---|---|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | Test | ||||
| Information Level | Reference | Upper | Trt | ||||
| Proportion | Actual | Upper | Beta | Alpha | Estimate | Action | |
| 1 | 0.2525 | 126.9871 | 0.15000 | -0.09306 | 0.27423 | 0.11111 | Continue |
| 2 | 0.5122 | 257.5571 | 0.15000 | 0.03019 | 0.17001 | 0.17593 | Reject Null |
| 3 | 0.7500 | 377.1257 | 0.15000 | 0.06783 | 0.11826 | . | |
| 4 | 1.0000 | 502.8343 | 0.15000 | 0.08878 | 0.08878 | . | |
With ODS Graphics enabled, the “Test Plot” is displayed, as shown in Output 84.1.16. The plot displays boundary values of the design and the test statistics at the first two stages. As expected, the test statistic at stage 2 is in the “Upper Rejection Region” above the upper alpha boundary.
Output 84.1.16: Sequential Test Plot
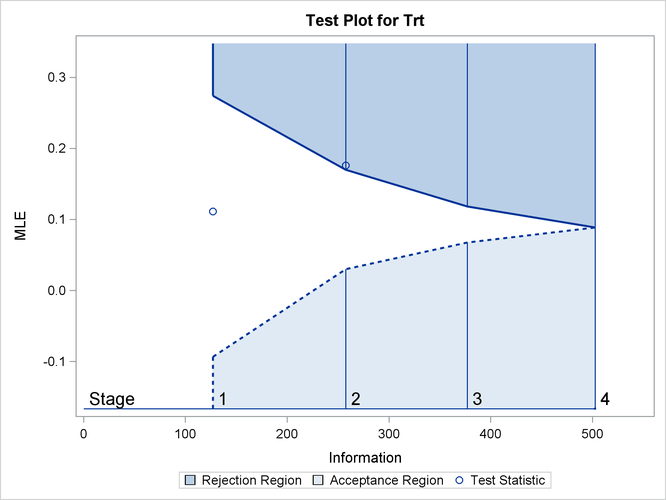
After a trial is stopped, the “Parameter Estimates” table in Output 84.1.17 displays the stopping stage and the maximum likelihood estimate of the parameter. It also displays the p-value, median estimate, and confidence limits for the parameter that correspond to the observed statistic by using the specified sample space ordering.
Output 84.1.17: Parameter Estimates
| Parameter Estimates Stagewise Ordering |
|||||
|---|---|---|---|---|---|
| Parameter | Stopping Stage |
MLE | p-Value for H0:Parm=0 |
Median Estimate |
Lower 95% CL |
| Trt | 2 | 0.175926 | 0.0031 | 0.174462 | 0.07059 |
The MLE statistic at the stopping stage is the maximum likelihood estimate of the parameter and is biased. The computation
of p-value, unbiased median estimate, and confidence limits depends on the ordering of the sample space ![]() , where k is the stage number and z is the observed standardized Z statistic. By default (or equivalently if you specify ORDER=STAGEWISE), the stagewise ordering that uses counterclockwise
ordering around the continuation region is used to compute the p-value, unbiased median estimate, and confidence limits. As expected, the p-value is less than 0.025, and the confidence interval does not contain the null reference zero. With the stagewise ordering,
the p-value is computed as
, where k is the stage number and z is the observed standardized Z statistic. By default (or equivalently if you specify ORDER=STAGEWISE), the stagewise ordering that uses counterclockwise
ordering around the continuation region is used to compute the p-value, unbiased median estimate, and confidence limits. As expected, the p-value is less than 0.025, and the confidence interval does not contain the null reference zero. With the stagewise ordering,
the p-value is computed as
|
|
where ![]() is the observed standardized Z statistic at stage 2,
is the observed standardized Z statistic at stage 2, ![]() is the standardized normal variate at stage 1,
is the standardized normal variate at stage 1, ![]() is the standardized normal variate at stage 2, and
is the standardized normal variate at stage 2, and ![]() and
and ![]() are the stage 1 upper rejection and acceptance boundary values, respectively.
are the stage 1 upper rejection and acceptance boundary values, respectively.
See the section Available Sample Space Orderings in a Sequential Test for a detailed description of the stagewise ordering.