The SURVEYLOGISTIC Procedure

Link Functions and the Corresponding Distributions

Four link functions are available in the SURVEYLOGISTIC procedure. The logit function is the default. To specify a different link function, use the LINK= option in the MODEL statement. The link functions and the corresponding distributions are as follows:

The logit function

$g(p)=\log \left( \frac{p}{1-p} \right)$

is the inverse of the cumulative logistic distribution function, which is

$F(x)=\frac{1}{1+e^{-x}}$

The probit (or normit) function

$g(p)=\Phi ^{-1}(p)$

is the inverse of the cumulative standard normal distribution function, which is

$F(x)=\Phi (x)=\frac{1}{\sqrt {2\pi }}\int _{-\infty }^ x e^{-\frac{1}{2} z^2} dz$

Traditionally, the probit function includes an additive constant 5, but throughout PROC SURVEYLOGISTIC, the terms probit and normit are used interchangeably, previously defined as .

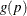The complementary log-log function

$g(p)=\log (-\log (1-p))$

is the inverse of the cumulative extreme-value function (also called the Gompertz distribution), which is

$F(x)=1-e^{-e^ x}$

The generalized logit function extends the binary logit link to a vector of levels 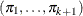$(\pi _1,\ldots ,\pi _{k+1})$ by contrasting each level with a fixed level

$g(\pi _ i)=\log \left( \frac{\pi _ i}{\pi _{k+1}} \right) \quad i=1,\ldots , k$

The variances of the normal, logistic, and extreme-value distributions are not the same. Their respective means and variances are

Distribution	Mean	Variance
Normal	0	1
Logistic	0	$\pi ^2/3$
Extreme-value	$-\gamma$	$\pi ^2/6$

where $\gamma$ is the Euler constant. In comparing parameter estimates that use different link functions, you need to take into account the different scalings of the corresponding distributions and, for the complementary log-log function, a possible shift in location. For example, if the fitted probabilities are in the neighborhood of 0.1 to 0.9, then the parameter estimates from using the logit link function should be about $\pi /\sqrt {3}\approx 1.8$ larger than the estimates from the probit link function.