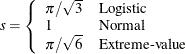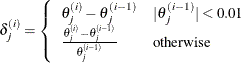The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Model Options
Model options can be specified after a slash (/). Table 91.7 summarizes the options available in the MODEL statement.
Table 91.7: MODEL Statement Options
|
Option |
Description |
|---|---|
|
Model Specification Options |
|
|
Specifies link function |
|
|
Suppresses intercept(s) |
|
|
Specifies offset variable |
|
|
Convergence Criterion Options |
|
|
Specifies absolute function convergence criterion |
|
|
Specifies relative function convergence criterion |
|
|
Specifies relative gradient convergence criterion |
|
|
Specifies relative parameter convergence criterion |
|
|
Specifies maximum number of iterations |
|
|
Suppresses checking for infinite parameters |
|
|
Specifies technique used to improve the log-likelihood function when its value is worse than that of the previous step |
|
|
Specifies tolerance for testing singularity |
|
|
Specifies iterative algorithm for maximization |
|
|
Options for Adjustment to Variance Estimation |
|
|
Chooses variance estimation adjustment method |
|
|
Options for Confidence Intervals |
|
|
Specifies |
|
|
Computes confidence intervals for parameters |
|
|
Computes confidence intervals for odds ratios |
|
|
Options for Display of Details |
|
|
Displays correlation matrix |
|
|
Displays covariance matrix |
|
|
Displays exponentiated values of estimates |
|
|
Displays iteration history |
|
|
Suppresses “Class Level Information” table |
|
|
Displays parameter labels |
|
|
Displays generalized |
|
|
Displays standardized estimates |
|
The following list describes these options: