Computational Formulas
Previous Page|Next Page

The CATMOD Procedure

Computational Formulas

Subsections:

The following formulas are shown for each population and for all populations combined.

 

Source

Formula

Dimension

Probability Estimates

 

jth response

$ p_{ij} = \displaystyle \frac{n_{ij}}{n_ i}$

$1 \times 1$

 

ith population

$\mb {p}_ i = \left[ \begin{array}{c} p_{i1} \\ p_{i2} \\ \vdots \\ p_{ir} \\ \end{array} \right]$

$r \times 1$

 

all populations

$\mb {p} = \left[ \begin{array}{c} \mb {p}_1 \\ \mb {p}_2 \\ \vdots \\ \mb {p}_ s \\ \end{array} \right]$

$sr \times 1$

Variance of Probability Estimates

 

ith population

$\mb {V}_ i = \displaystyle \frac{1}{n_ i} (\mb {{DIAG}}(\mb {p}_ i) - \mb {p}_ i \mb {p}_ i{’})$

$r \times r$

 

all populations

$\mb {V} = \mb {{DIAG}}(\mb {V}_1, \mb {V}_2, \ldots , \mb {V}_ s )$

$sr \times sr$

Response Functions

ith population

$\mb {F}_ i = \mb {F}(\mb {p}_ i)$

$q \times 1$

 

all populations

$\mb {F} = \left[ \begin{array}{c} \mb {F}_1 \\ \mb {F}_2 \\ \vdots \\ \mb {F}_ s \\ \end{array} \right]$

$sq \times 1$

Derivative of Function with Respect to Probability Estimates

 

ith population

$\mb {H}_ i = \displaystyle \frac{\partial \mb {F}(\mb {p}_ i)}{\partial \mb {p}_ i}$

$q \times r$

 

all populations

$\mb {H} = \mb {{DIAG}}(\mb {H}_1, \mb {H}_2, \ldots , \mb {H}_ s )$

$sq \times sr$

Variance of Functions

ith population

$\mb {S}_ i = \mb {H}_ i \mb {V}_ i \mb {H}_ i{’}$

$q \times q$

 

all populations

$\mb {S} = \mb {{DIAG}}(\mb {S}_1, \mb {S}_2, \ldots , \mb {S}_ s )$

$sq \times sq$

Inverse Variance of Functions

ith population

$\mb {S}^ i = (\mb {S}_ i)^{-1}$

$q \times q$

 

all populations

$\mb {S}^{-1} = \mb {{DIAG}}(\mb {S}^1, \mb {S}^2, \ldots , \mb {S}^ s )$

$sq \times sq$

Derivative Table for Compound Functions: Y=F(G(p))

In the following table, let $\mb {G}(\mb {p})$ be a vector of functions of $\mb {p}$, and let $\mb {D}$ denote $\partial \mb {G} / \partial \mb {p}$, which is the first derivative matrix of $\mb {G}$ with respect to $\mb {p}$:

Function

$\mb {Y} = \mb {F}(\mb {G})$

Derivative $(\partial \mb {Y} / \partial \mb {p})$

Multiply matrix

$\mb {Y} = \mb {A}*\mb {G}$

$\mb {A}*\mb {D}$

Logarithm

$\mb {Y} = \mb {{LOG}}(\mb {G})$

$\mb {{DIAG}}^{-1}(\mb {G})*\mb {D}$

Exponential

$\mb {Y} = \mb {{EXP}}(\mb {G})$

$\mb {{DIAG}}(\mb {Y})*\mb {D}$

Add constant

$\mb {Y} = \mb {G} + \mb {A}$

$\mb {D}$

Default Response Functions: Generalized Logits

In the following table, subscripts i for the population are suppressed. Also denote $\displaystyle f_ j = \log \left( \frac{p_ j}{p_ r} \right)$ for $j = 1, \ldots , r-1$ for each population $i = 1, \ldots , s $.

 

Formula

Inverse of Response Functions for a Population

 

$\begin{array}{rcl} \displaystyle p_ j & = & \displaystyle \frac{\exp (f_ j)}{1 + \sum _ k \exp (f_ k)} ~ ~ \mbox{ for } j = 1, \ldots , r-1 \\*[0.10in] p_ r & = & \displaystyle \frac{1}{1 + \sum _ k \exp (f_ k)} \end{array}$

Form of F and Derivative for a Population

 

$\begin{array}{rcl} \mb {F} & = & \mb {{K LOG}}(\mb {p}) = (\mb {I}_{r-1}, -\mb {j}) ~ \mb {{LOG}} (\mb {p}) \\*[0.10in] \mb {H} & = & \displaystyle \frac{\partial \mb {F}}{\partial \mb {p}} = \left( \mb {{DIAG}}_{r-1}^{-1} (\mb {p}), \frac{-1}{p_ r} \mb {j} \right) \end{array}$

Covariance Results for a Population

 

$\begin{array}{rcl} \mb {S} & = & \mb {HVH}{’} \\*[0.05in]& = & \displaystyle \frac{1}{n} \left( \mb {{DIAG}}_{r-1}^{-1}(\mb {p}) + \frac{1}{p_ r} \mb {J}_{r-1} \right) \\*& & \mbox{ where } \mb {V}, \mb {H}, \mbox{ and } \mb {J} \mbox{ are as previously defined.} \\*[0.10in] \mb {S}^{-1} & = & n (\mb {{DIAG}}_{r-1}(\mb {p}) - \mb {qq}{’}) \quad \mbox{, where } \mb {q} = \mb {{DIAG}}_{r-1}(\mb {p}) ~ \mb {j} \\*[0.10in] \mb {S}^{-1}\mb {F} & = & \displaystyle n \mb {{DIAG}}_{r-1}(\mb {p})\mb {F} - (n \sum _ j p_ j f_ j) ~ \mb {q} \\*[0.10in] \mb {F}{’}\mb {S}^{-1}\mb {F} & = & \displaystyle n \sum _ j p_ j f_ j^2 - n (\sum _ j p_ j f_ j)^2 \end{array}$

The following calculations are shown for each population and then for all populations combined:

 

Source

Formula

Dimension

Design Matrix

ith population

$\mb {X}_ i$

$q \times d$

 

all populations

$\mb {X} = \left[ \begin{array}{c} \mb {X}_1 \\ \mb {X}_2 \\ \vdots \\ \mb {X}_ s \\ \end{array} \right]$

$sq \times d$

Crossproduct of Design Matrix

 

ith population

$\mb {C}_ i = \mb {X}_ i{’} \mb {S}^ i \mb {X}_ i$

$d \times d$

 

all populations

$\mb {C} = \mb {X}{’} \mb {S}^{-1} \mb {X} = \sum _ i \mb {C}_ i$

$d \times d$

In the following table, $z_ p$ is the 100pth percentile of the standard normal distribution:

 

Formula

Dimension

Crossproduct of Design Matrix with Function

 

$\mb {R} = \mb {X}{’} \mb {S}^{-1} \mb {F} = \sum _ i \mb {X}_ i{’} \mb {S}^ i \mb {F}_ i$

$d \times 1$

Weighted Least Squares Estimates

$\mb {b} = \mb {C}^{-1} \mb {R} = (\mb {X}{’} \mb {S}^{-1} \mb {X})^{-1} (\mb {X}{’} \mb {S}^{-1} \mb {F})$

$d \times 1$

Covariance of Weighted Least Squares Estimates

 

$\mb {{COV}}(\mb {b}) = \mb {C}^{-1}$

$d \times d$

Wald Confidence Limits for Parameter Estimates

 

$b_{k} \pm z_{1-\alpha /2}\mb {C}^{-1}_{kk}$

$k=1,\dots , d$

Predicted Response Functions

 

$\mb {\hat{F}} = \mb {Xb}$

$sq \times 1$

Covariance of Predicted Response Functions

 

$\mb {V_{\hat{F}}} = \mb {X}\mb {C}^{-1}\mb {X}{’}$

$sq \times sq$

Residual Chi-Square

 

RSS $= \mb {F}{’} \mb {S}^{-1} \mb {F} - \mb {\hat{F}}{’} \mb {S}^{-1} \mb {\hat{F}}$

$1 \times 1$

Chi-Square for $H_0\colon \mb {L} \bbeta = \mb {0}$

 

Q $= (\mb {Lb}){’} (\mb {LC}^{-1} \mb {L}{’})^{-1} (\mb {Lb})$

$1 \times 1$

Maximum Likelihood Method

Let $\mb {C}$ be the Hessian matrix and $\mb {G}$ be the gradient of the log-likelihood function (both functions of $\bpi $ and the parameters $\bbeta $). Let $\mb {p}_ i^*$ denote the vector containing the first $r-1$ sample proportions from population i, and let $\bpi _ i^*$ denote the corresponding vector of probability estimates from the current iteration. Starting with the least squares estimates $\mb {b}_0$ of $\bbeta $ (if you use the ML and WLS options; with the ML option alone, the procedure starts with $\mb {0}$), the probabilities $\bpi (\mb {b})$ are computed, and $\mb {b}$ is calculated iteratively by the Newton-Raphson method until it converges (see the EPSILON= option). The factor $\lambda $ is a step-halving factor that equals one at the start of each iteration. For any iteration in which the likelihood decreases, PROC CATMOD uses a series of subiterations in which $\lambda $ is iteratively divided by two. The subiterations continue until the likelihood is greater than that of the previous iteration. If the likelihood has not reached that point after 10 subiterations, then convergence is assumed, and a warning message is displayed.

Sometimes, infinite parameters are present in the model, either because of the presence of one or more zero frequencies or because of a poorly specified model with collinearity among the estimates. If an estimate is tending toward infinity, then PROC CATMOD flags the parameter as infinite and holds the estimate fixed in subsequent iterations. PROC CATMOD regards a parameter to be infinite when two conditions apply:

  • The absolute value of its estimate exceeds five divided by the range of the corresponding variable.

  • The standard error of its estimate is at least three times greater than the estimate itself.

The estimator of the asymptotic covariance matrix of the maximum likelihood predicted probabilities is given by Imrey, Koch, and Stokes (1981, eq. 2.18).

The following equations summarize the method:

\[ \mb {b}_{k+1} = \mb {b}_ k - \lambda \mb {C}^{-1} \mb {G} \]

where

\begin{eqnarray*} \mb {C} & = & \mb {X}{’}\mb {S}^{-1}(\bpi ) \mb {X} \\[0.10in] \mb {N} & = & \left[ \begin{array}{c} n_1 ( \mb {p}_1^* - \bpi _1^* ) \\ \vdots \\ n_ s ( \mb {p}_ s^* - \bpi _ s^* ) \\ \end{array} \right] \\ \mb {G} & = & \mb {X}{’}\mb {N} \\ \end{eqnarray*}

Iterative Proportional Fitting

The algorithm used by PROC CATMOD for iterative proportional fitting is described in Bishop, Fienberg, and Holland (1975); Haberman (1972); Agresti (2002). To illustrate the method, consider the observed three-dimensional table $\{ n_{ijk}\} $ for the variables X, Y, and Z, and the following hierarchical model:

\[ \log (m_{ijk}) = \mu + \lambda _ i^ X + \lambda _ j^ Y + \lambda _ k^ Z + \lambda _{ij}^{XY} + \lambda _{ik}^{XZ} + \lambda _{jk}^{YZ} \]

The following statements request that PROC CATMOD use IPF to fit the preceding model: 

model X*Y*Z = _response_ / ml=ipf;
loglin X|Y|Z@2;

Begin with a table of initial cell estimates $\{ \hat m_{ijk}^{(0)}\} $. PROC CATMOD produces the initial estimates by setting the $n_{sz}$ structural zero cells to 0 and all other cells to $n/(n_ c-n_{sz})$, where n is the total weight of the table and $n_ c$ is the total number of cells in the table. Iteratively adjust the estimates at step $s-1$ to the observed marginal tables specified in the model by cycling through the following three-stage process to produce the estimates at step s:

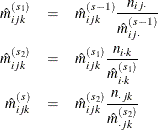
\begin{eqnarray*} \hat m_{ijk}^{(s_1)} & =& \hat m_{ijk}^{(s-1)}\frac{n_{ij\cdot } }{\hat m_{ij\cdot }^{(s-1)}}\\ \hat m_{ijk}^{(s_2)} & =& \hat m_{ijk}^{(s_1)}\frac{n_{i\cdot k}}{\hat m_{i\cdot k}^{(s_1)}}\\ \hat m_{ijk}^{(s)} & =& \hat m_{ijk}^{(s_2)}\frac{n_{\cdot jk}}{\hat m_{\cdot jk}^{(s_2)}}\\ \end{eqnarray*}

The subscript “$\cdot $” indicates summation over the missing subscript. The log-likelihood $l_ s$ is estimated at each step s by

\[ l_ s = \sum _{i,j,k} n_{ijk}\log \left(\frac{\hat m_{ijk}^{(s)}}{n}\right) \]

When the function $|(l_{s-1}-l_{s})/l_{s-1}|$ is less than $10^{-8}$, the iterations terminate. You can change the comparison value with the EPSILON= option, and you can change the convergence criterion with the CONVCRIT= option. The option CONVCRIT=CELL uses the maximum cell difference

\[ \max _{i,j,k}|\hat m_{ijk}^{(s-1)}-\hat m_{ijk}^{(s)}| \]

as the criterion while the option CONVCRIT=MARGIN computes the maximum difference of the margins

\[ \mbox{Maximum of}\left\{ \max _{i,j}|\hat m_{ij\cdot }^{(s-1)}-\hat m_{ij\cdot }^{(s)}| , \max _{i,k}|\hat m_{i\cdot k}^{(s-1)}-\hat m_{i\cdot k}^{(s)}| , \max _{j,k}|\hat m_{\cdot jk}^{(s-1)}-\hat m_{\cdot jk}^{(s)}| \right\} \]
Previous Page|Next Page|Top of Page
Copyright © SAS Institute Inc. All Rights Reserved.