The GLMPOWER Procedure
REPEATED factor-specification ;
If the MODEL statement includes more than one dependent variable, you can indicate a multivariate model and define transformations of dependent variables by using the REPEATED statement.
The REPEATED statement enables you to define custom Type III hypothesis tests by choosing from among several transformations of the dependent
variables: contrast, Helmert, identity, mean, polynomial, and profile. Each of these transformations produces an ![]() vector or matrix for testing the hypothesis
vector or matrix for testing the hypothesis ![]() . The
. The ![]() matrix consists of one or more within-subject contrasts.
matrix consists of one or more within-subject contrasts.
To use this feature, you must be familiar with the details of multivariate model and contrast parameterizations that PROC GLM uses. For more information, see the sections Repeated Measures Analysis of Variance and Multivariate Analysis of Variance in Chapter 44: The GLM Procedure. For information about the power and sample size computational methods and formulas, see the section Contrasts in Fixed-Effect Multivariate Models.
If you specify one or more REPEATED statements, then a “Mean(Dep)” transformation is added to the power analysis. This transformation is the mean of the dependent variables, the same transformation that is used implicitly in the “Tests of Hypotheses for Between Subjects Effects” table in PROC GLM. In addition, the Intercept model effect is included in the power analysis. If the REPEATED statement is not specified, then tests that involve the Intercept are excluded from the power analysis.
You can use either the REPEATED statement or the MANOVA statement along with any of the tests for multivariate models that are supported in the MTEST= option in the POWER statement. The REPEATED statement is usually used for handling repeated measurements on the same experimental unit, but you can also use the REPEATED statement for other situations, such as clusters or multiple outcome variables. The differences between the REPEATED and MANOVA statements are as follows:
-
You can use the REPEATED statement to specify commonly used contrasts by using keywords rather than coefficients, but you are limited to only those forms of the
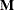 matrix.
matrix.
-
You can use the MANOVA statement to construct any
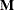 matrix, but you must specify the coefficients explicitly (except for the default identity matrix).
matrix, but you must specify the coefficients explicitly (except for the default identity matrix).
There is no limit to the number of REPEATED statements that you can specify. Each power analysis includes tests for all REPEATED statements and also (if you specify at least one REPEATED statement) the extra “Mean(Dep)” transformation that was previously mentioned.
The simplest form of the REPEATED statement requires only a factor-name. Optionally, you can specify the actual values for the levels (level-values) and a transformation that defines single-degree-of-freedom contrasts.
The factor-specification for the REPEATED statement has the following form:
factor-name < (level-values)> <transformation>
- factor-name
-
names a factor to be associated with the dependent variables. The name should not be the same as any variable name that already exists in the data set being analyzed and should conform to the usual conventions of SAS variable names.
- (level-values)
-
gives values that correspond to levels of a repeated measures factor. The number of levels must be the same as the number of dependent variables in the model. These values are used as spacings for constructing orthogonal polynomial contrasts if you specify a POLYNOMIAL transformation. Enclose the level-values in parentheses.
The following transformation keywords define single-degree-of-freedom contrasts. Because the number of contrasts that are generated is always one less than the number of levels of the factor, you have some control over which contrast is omitted from the analysis by which transformation you select. The only exception is the IDENTITY transformation, which is not composed of contrasts and has the same degrees of freedom as the factor has levels. By default, PROC GLMPOWER uses the CONTRAST transformation.
