The IRT Procedure (Experimental)

PROC IRT Statement

Subsections:

PROC IRT Statement Options

PROC IRT <options> ;

The PROC IRT statement invokes the IRT procedure. Table 51.1 summarizes the options available in the PROC IRT statement. The sections that follow the table describe the PROC IRT statement options and then describe the other statements in alphabetical order.

These options in the PROC IRT statement are then described fully in alphabetical order.

Table 51.1: PROC IRT Statement Options

Option	Description
Basic Options
DATA=	Specifies the input data set
DESCENDING	Reverses the sort order of the levels of the response variable
ITEMFIT	Computes the item fit statistics and displays them in a table
LINK=	Specifies the link function
NFACTOR=	Specifies the number of factors
OUT=	Specifies the output data set for factor scores
RESFUNC=	Specifies the response function
RORDER=	Specifies the sort order of the response variables
SCOREMETHOD=	Specifies the factor score estimation method
Computational Options
ABSFCONV=	Specifies an absolute function difference convergence criterion
ABSGCONV=	Specifies an absolute gradient convergence criterion
ABSPCONV=	Specifies a maximum absolute parameter difference convergence criterion
FCONV=	Specifies a relative function convergence criterion
GCONV=	Specifies a relative gradient convergence criterion
MAXFUNC=	Specifies the maximum number of function calls in the optimization process
MAXITER=	Specifies the maximum number of iterations in the optimization process
MAXMITER=	Specifies the maximum number of iterations in the maximization step of the EM algorithm
NOAD	Specifies nonadaptive quadrature
QPOINTS=	Specifies the number of quadrature points per dimension
TECHNIQUE=	Specifies the optimization technique to obtain maximum likelihood estimates.
Display Options
NOITPRINT	Suppresses the display of the “Iteration History” table
NOPRINT	Suppresses all ODS output
PINITIAL	Displays initial parameter estimates
PLOTS=	Controls plots that are produced through ODS Graphics
Rotation Method and Properties
RCONVERGE=	Specifies the convergence criterion for rotation cycles
RITER=	Specifies the maximum number of rotation cycles
ROTATE=	Specifies the rotation method

PROC IRT Statement Options

ABSFCONV=r ABSFTOL=r

specifies an absolute function difference convergence criterion. Termination requires a small change of the function value in successive iterations,

$|f(\bpsi ^{(k-1)}) - f(\bpsi ^{(k)})| \leq r$

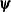where $\bpsi$ denotes the vector of parameters that participate in the optimization and 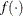$f(\cdot )$ is the objective function. This criterion is not used by the expectation-maximization (EM) algorithm. By default, r = 0.

ABSGCONV=r ABSGTOL=r

specifies an absolute gradient convergence criterion. Termination requires the maximum absolute gradient element to be small,

$\max _ j |g_ j(\bpsi ^{(k)})| \leq r$

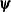where $\bpsi$ denotes the vector of parameters that participate in the optimization and 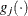$g_ j(\cdot )$ is the gradient of the objective function with respect to the jth parameter. This criterion is not used by the EM algorithm. By default, r = 1E–5.

ABSPCONV=r ABSPTOL=r

specifies a maximum absolute parameter difference convergence criterion. This criterion is used only by the EM algorithm. Termination requires the maximum absolute parameter change in successive iterations to be small,

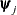$\max _ j|\bpsi _ j^{(k-1)} - \bpsi _ j^{(k)}| \leq r$

where $\bpsi _ j$ denotes the jth parameter that participates in the optimization. By default, r = 1E–4.

DATA=SAS-data-set

specifies the SAS-data-set to be read by PROC IRT. The default value is the most recently created data set.

DESCENDING DESC

reverses the sorting order for the levels of the response variables. If both the DESCENDING and RORDER= options are specified, PROC IRT orders the levels according to the RORDER= option and then reverses that order.

FCONV=r FTOL=r

specifies a relative function convergence criterion. Termination requires a small relative change of the function value in successive iterations,

$\frac{|f(\bpsi ^{(k)}) - f(\bpsi ^{(k-1)})|}{|f(\bpsi ^{(k-1)})|} \leq r$

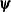where $\bpsi$ denotes the vector of parameters that participate in the optimization and 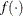$f(\cdot )$ is the objective function. This criterion is not used by the EM algorithm. By default, r 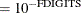$=10^{-\mr {FDIGITS}}$ , where FDIGITS is, by default, 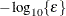$-\log _{10}\{ \epsilon \}$ and $\epsilon$ is the machine precision.

GCONV=r GTOL=r

specifies a relative gradient convergence criterion. For all techniques except CONGRA, termination requires the normalized predicted function reduction to be small,

$\frac{\mb {g}(\bpsi ^{(k)})^\prime [\bH ^{(k)}]^{-1} \mb {g}(\bpsi ^{(k)})}{|f(\bpsi ^{(k)})| } \leq r$

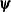where $\bpsi$ denotes the vector of parameters that participate in the optimization, 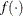$f(\cdot )$ is the objective function, and 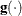$\mb {g}(\cdot )$ is the gradient. For the CONGRA technique (for which a reliable Hessian estimate 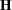$\bH$ is not available), the following criterion is used:

$\frac{\parallel \mb {g}(\bpsi ^{(k)}) \parallel _2^2 \quad \parallel \mb {s}(\bpsi ^{(k)}) \parallel _2}{\parallel \mb {g}(\bpsi ^{(k)}) - \mb {g}(\bpsi ^{(k-1)}) \parallel _2 |f(\bpsi ^{(k)})| } \leq r$

This criterion is not used by the EM algorithm. By default, r = 1E–8.

ITEMFIT

calculates and displays the item fit statistics. These item fit statistics apply only to binary items that have one latent factor.

LINK=name

specifies the link function. You can specify the following link functions:

LOGIT: requests the logistic link function.
PROBIT: requests the probit link function.

By default, LINK=LOGIT.

MAXFUNC=n MAXFU=n

specifies the maximum number of function calls in the optimization process. This option is not used by the EM algorithm. The default values are as follows, depending on the optimization technique:

NRRIDG: 125
QUANEW: 500
CONGRA: 1000

The optimization can terminate only after completing a full iteration. Therefore, the number of function calls that are actually performed can exceed the number that is specified by this option. You can select the optimization technique by specifying the TECHNIQUE= option.

MAXITER=n MAXIT=n

specifies the maximum number of iterations in the optimization process. The default values are as follows, depending on the optimization technique:

NRRIDG: 50
QUANEW: 200
CONGRA: 400
EM: 500

MAXMITER=n MAXMIT=n

specifies the maximum number of iterations in the maximization step of the EM algorithm. By default, n = 1.

NFACTOR=i NFACT=i

specifies the number of factors, i, in the model. You must specify the number of factors only for exploratory analysis, in which all the slope parameters of the items are freely estimated without being explicitly constrained by using the FACTOR statement. By default, NFACTOR=1. When you use the FACTOR statement to specify the confirmatory factor pattern, the number of factors is implicitly defined by the number of distinctive factor names that you specify in the statement.

NOAD

requests that the Gaussian quadrature be nonadaptive.

NOITPRINT

suppresses the display of the “Iteration History” table.

NOPRINT

suppresses all output displays.

specifies the optimization technique to obtain maximum likelihood estimates. You can specify the following techniques:

CONGRA: performs a conjugate-gradient optimization.
EM: performs an EM optimization.
NONE: performs no optimization.
NRRIDG: performs a Newton-Raphson optimization with ridging.
QUANEW: performs a dual quasi-Newton optimization.

By default, TECHNIQUE=QUANEW.

For more information about these optimization methods (except EM), see the section Choosing an Optimization Algorithm in Chapter 19: Shared Concepts and Topics. For more information about the EM algorithm, see “Expectation-Maximization (EM) Algorithm” in the section Details: IRT Procedure.

OUT=SAS-data-set

creates an output data set that contains all the data in the DATA= data set plus estimated factor scores. For exploratory analysis, the factor scores are named _Factor1, _Factor2, and so on. For confirmatory analysis, user-specified factor names are used.

PROC IRT provides three estimation methods for factor scores. You can specify the method by using the SCOREMETHOD option. The default estimation method, maximum a posteriori (MAP), is used if the SCOREMETHOD option is not specified.

PINITIAL

displays the initial parameter estimates.

PLOTS <(global-plot-options)> <= plot-request <(options)>> PLOTS <(global-plot-options)> <= (plot-request <(options)> <…plot-request <(options)>>)>

controls the plots that are produced through ODS Graphics. When you specify only one plot-request, you can omit the parentheses around it. For example:

plots=all
plots=ICC(unpack)
plots(unpack)=(scree ICC)

ODS Graphics must be enabled before plots can be requested. For example:

ods graphics on;
proc irt plots=all;
run;
ods graphics off;

For more information about enabling and disabling ODS Graphics, see the section Enabling and Disabling ODS Graphics in Chapter 21: Statistical Graphics Using ODS.

You can specify the following global-plot-option, which applies to all plots that the IRT procedure generates:

UNPACK |UNPACKPANEL: suppresses paneling. By default, multiple plots can appear in some output panels. Specify UNPACK to display each plot individually. You can also specify UNPACK as a suboption in the ICC and SCREE options.

You can specify the following plot-requests:

ALL: displays all default plots.
SCREE <(UNPACK |UNPACKPANEL)>: displays the scree and variance explained plots in the same panel. You can display these plots individually by specifying the UNPACK suboption.
ICC <(UNPACK |UNPACKPANEL)>: displays item characteristic curve (ICC) plots. By default, multiple ICC plots appear in some output panels. You can request an individual ICC plot for each item by specifying the UNPACK suboption.
NONE: suppresses all plots.

QPOINTS=i

specifies the number of quadrature points in each dimension of the integral. Note that if there are d latent factors and n quadrature points, the IRT procedure evaluates 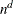$n^ d$ conditional log likelihoods for each observation to compute one value of the objective function. Increasing the number of quadrature nodes can substantially increase the computational burden. If you do not specify the number of quadrature points, it is determined adaptively by using the initial parameter estimates.

RCONVERGE=p RCONV=p

specifies the convergence criterion for rotation cycles. Rotation stops when the scaled change of the simplicity function value is less than the RCONVERGE= value. The default convergence criterion is

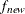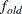$|f_{\mathit{new}}-f_{\mathit{old}}|/K < \epsilon$

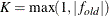where ${f}_{\mathit{new}}$ and ${f}_{\mathit{old}}$ are simplicity function values of the current cycle and the previous cycle, respectively; $K=\max (1,|{f}_{\mathit{old}}|)$ is a scaling factor; and $\epsilon$ is 1E–9 by default and is modified by the RCONVERGE= value.

specifies the response functions for the variables that are included in the VAR statement. The response functions correspond to different response models. The graded response (GRADED) model is assumed by default. You can specify the following response functions:

ONEP: specifies the one-parameter model.
TWOP: specifies the two-parameter model.
THREEP: specifies the three-parameter model.
FOURP: specifies the four-parameter model.
GRADED: specifies the graded response model.
RASCH: specifies the Rasch model.

The graded response model assumes that the response variables are ordinal-categorical up to 19 levels. All other models assume binary responses. For more information about these response models, see “Response Models” in the Details: IRT Procedure section.

RITER=n

specifies the maximum number of cycles for factor rotation. The default value is the maximum between 10 times the number of variables and 100.

ROTATE=name R=name

specifies the rotation method. You can specify the following orthogonal rotation methods:

BIQUARTIMAX | BIQMAX: specifies orthogonal biquartimax rotation.
EQUAMAX | E: specifies orthogonal equamax rotation.
NONE | N: specifies that no rotation be performed, leaving the original orthogonal solution.
PARSIMAX | PA: specifies orthogonal parsimax rotation.
QUARTIMAX | QMAX | Q: specifies orthogonal quartimax rotation.
VARIMAX | V: specifies orthogonal varimax rotation.

You can specify the following oblique rotation methods:

OBBIQUARTIMAX | OBIQMAX: specifies oblique biquartimax rotation.
OBEQUAMAX | OE: specifies oblique equamax rotation.
OBPARSIMAX | OPA: specifies oblique parsimax rotation.
OBQUARTIMAX | OQMAX: specifies oblique quartimax rotation.
OBVARIMAX | OV: specifies oblique varimax rotation.

By default, ROTATE=VARIMAX.

RORDER=DATA | FORMATTED | FREQ | INTERNAL

specifies the sort order for the levels of the response variable. This order determines which threshold parameter in the model corresponds to each level in the data. If RORDER=FORMATTED for numeric variables for which you have supplied no explicit format, the levels are ordered by their internal values. This option applies to all the responses in the model. When the default, RORDER=FORMATTED, is in effect for numeric variables for which you have supplied no explicit format, the levels are ordered by their internal values. You can specify the following sort orders:

Value of RORDER=	Levels Sorted By
DATA	Order of appearance in the input data set
FORMATTED	External formatted value, except for numeric variables that have no explicit format, which are sorted by their unformatted (internal) value
FREQ	Descending frequency count; levels that contain the most observations come first in the order
INTERNAL	Unformatted value

For FORMATTED and INTERNAL, the sort order is machine-dependent. For more information about sort order, see the chapter on the SORT procedure in the SAS Procedures Guide and the discussion of BY-group processing in SAS Language Reference: Concepts.

SCOREMETHOD=ML | EAP | MAP

specifies the method of factor score estimation. You can specify the following methods:

ML: requests the maximum likelihood method.
EAP: requests the expected a posteriori method.
MAP: requests the maximum a posteriori method.