The MCMC Procedure

Example 59.21 Gelman-Rubin Diagnostics

PROC MCMC does not have the Gelman-Rubin test (see the section Gelman and Rubin Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures,) as a part of its diagnostics. The Gelman-Rubin diagnostics rely on parallel chains to test whether they all converge to the same posterior distribution. This example demonstrates how you can carry out this convergence test. The regression model from the section Simple Linear Regression is used. The model has three parameters: $\beta _0$ and $\beta _1$ are the regression coefficients, and $\sigma ^2$ is the variance of the error distribution.

The following statements generate the data set:

title 'Simple Linear Regression, Gelman-Rubin Diagnostics';

data Class;
   input Name $ Height Weight @@;
   datalines;
Alfred  69.0 112.5   Alice  56.5  84.0   Barbara 65.3  98.0
Carol   62.8 102.5   Henry  63.5 102.5   James   57.3  83.0
Jane    59.8  84.5   Janet  62.5 112.5   Jeffrey 62.5  84.0
John    59.0  99.5   Joyce  51.3  50.5   Judy    64.3  90.0
Louise  56.3  77.0   Mary   66.5 112.0   Philip  72.0 150.0
Robert  64.8 128.0   Ronald 67.0 133.0   Thomas  57.5  85.0
William 66.5 112.0
;

To run a Gelman-Rubin diagnostic test, you want to start Markov chains at different places in the parameter space. Suppose you want to start $\beta _0$ at 10, –15, and 0; $\beta _1$ at –5, 10, and 0; and $\sigma ^2$ at 1, 20, and 50. You can put these starting values in the following Init SAS data set:

data init;
   input Chain beta0 beta1 sigma2;
   datalines;
   1   10  -5   1
   2  -15  10  20
   3    0   0  50
;

The following statements run PROC MCMC three times, each with starting values specified in the data set Init:

/* define constants */
%let nchain = 3;
%let nparm = 3;
%let nsim = 50000;
%let var = beta0 beta1 sigma2;

%macro gmcmc;
   %do i=1 %to &nchain;
      data _null_;
         set init;
         if Chain=&i;
         %do j = 1 %to &nparm;
            call symputx("init&j", %scan(&var, &j));
         %end;
         stop;
      run;

      proc mcmc data=class outpost=out&i init=reinit nbi=0 nmc=&nsim
                stats=none seed=7;
         parms beta0 &init1 beta1 &init2;
         parms sigma2 &init3 / n;
         prior beta0 beta1 ~ normal(0, var = 1e6);
         prior sigma2 ~ igamma(3/10, scale = 10/3);
         mu = beta0 + beta1*height;
         model weight ~ normal(mu, var = sigma2);
      run;
   %end;
%mend;

ods listing close;
%gmcmc;
ods listing;

The macro variables nchain, nparm, nsim, and var define the number of chains, the number of parameters, the number of Markov chain simulations, and the parameter names, respectively. The macro GMCMC gets initial values from the data set Init, assigns them to the macro variables init1, init2 and init3, starts the Markov chain at these initial values, and stores the posterior draws to three output data sets: Out1, Out2, and Out3.

In the PROC MCMC statement, the INIT=REINIT option restarts the Markov chain after tuning at the assigned initial values. No burn-in is requested.

You can use the autocall macro GELMAN to calculate the Gelman-Rubin statistics by using the three chains. The GELMAN macro has the following arguments:

%macro gelman(dset, nparm, var, nsim, nc=3, alpha=0.05);

The argument dset is the name of the data set that stores the posterior samples from all the runs, nparm is the number of parameters, var is the name of the parameters, nsim is the number of simulations, nc is the number of chains with a default value of 3, and alpha is the $\alpha$ significant level in the test with a default value of 0.05. This macro creates two data sets: _Gelman_Ests stores the diagnostic estimates and _Gelman_Parms stores the names of the parameters.

The following statements calculate the Gelman-Rubin diagnostics:

data all;
   set out1(in=in1) out2(in=in2) out3(in=in3);
   if in1 then Chain=1;
   if in2 then Chain=2;
   if in3 then Chain=3;
run;

%gelman(all, &nparm, &var, &nsim);

data GelmanRubin(label='Gelman-Rubin Diagnostics');
   merge _Gelman_Parms _Gelman_Ests;
run;

proc print data=GelmanRubin;
run;

The Gelman-Rubin statistics are shown in Output 59.21.1.

Output 59.21.1: Gelman-Rubin Diagnostics of the Regression Example

Simple Linear Regression, Gelman-Rubin Diagnostics

Obs	Parameter	Between-chain	Within-chain	Estimate	UpperBound
1	beta0	5384.76	1168.64	1.0002	1.0001
2	beta1	1.20	0.30	1.0002	1.0002
3	sigma2	8034.41	2890.00	1.0010	1.0011

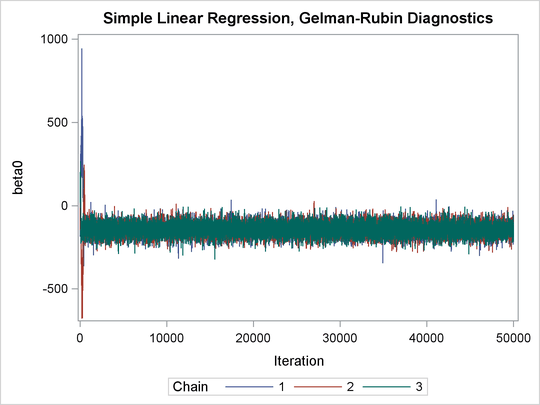
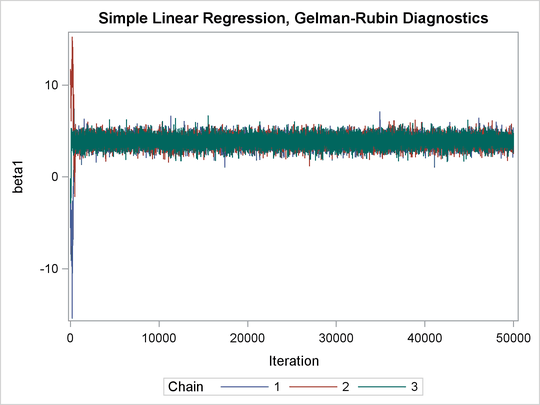
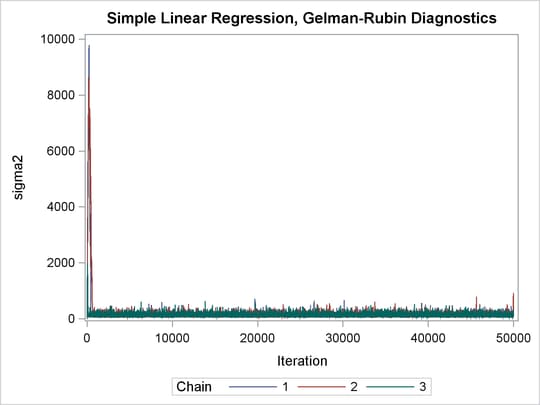
The Gelman-Rubin statistics do not reveal any concerns about the convergence or the mixing of the multiple chains. To get a better visual picture of the multiple chains, you can draw overlapping trace plots of these parameters from the three Markov chains runs.

The following statements create Output 59.21.2:

/* plot the trace plots of three Markov chains. */
%macro trace;
   %do i = 1 %to &nparm;
      proc sgplot data=all cycleattrs;
         series x=Iteration y=%scan(&var, &i) / group=Chain;
      run;
   %end;
%mend;
%trace;

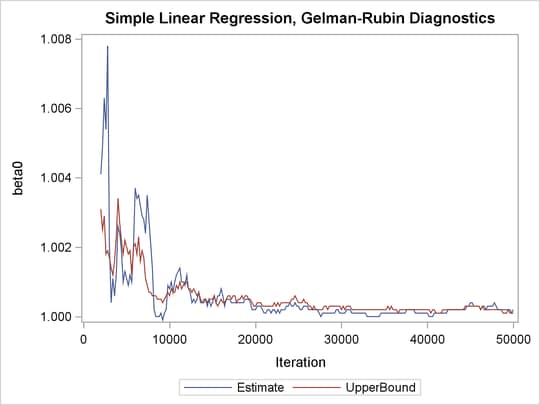
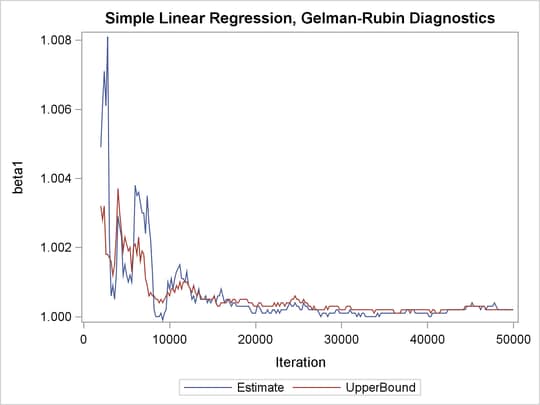
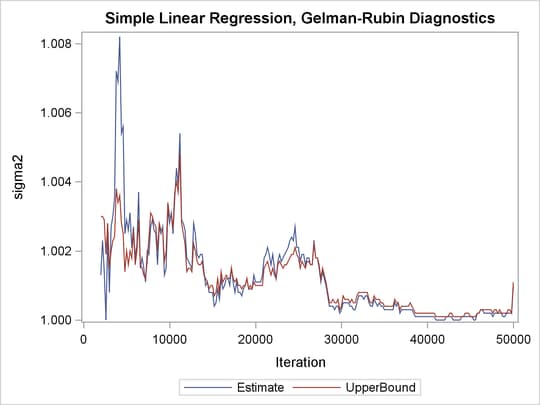
Output 59.21.2: Trace Plots of Three Chains for Each of the Parameters

The trace plots show that three chains all eventually converge to the same regions even though they started at very different locations. In addition to the trace plots, you can also plot the potential scale reduction factor (PSRF). See the section Gelman and Rubin Diagnostics in Chapter 7: Introduction to Bayesian Analysis Procedures, for definition and details.

The following statements calculate PSRF for each parameter. They use the GELMAN macro repeatedly and can take a while to run:

/* define sliding window size */
%let nwin = 200;
data PSRF;
run;

%macro PSRF(nsim);
   %do k = 1 %to %sysevalf(&nsim/&nwin, floor);
      %gelman(all, &nparm, &var, nsim=%sysevalf(&k*&nwin));
      data GelmanRubin;
         merge _Gelman_Parms _Gelman_Ests;
      run;

      data PSRF;
         set PSRF GelmanRubin;
      run;
   %end;
%mend PSRF;

options nonotes;
%PSRF(&nsim);
options notes;

data PSRF;
   set PSRF;
   if _n_ = 1 then delete;
run;

proc sort data=PSRF;
   by Parameter;
run;

%macro sepPSRF(nparm=, var=, nsim=);
   %do k = 1 %to &nparm;
      data save&k; set PSRF;
         if _n_ > %sysevalf(&k*&nsim/&nwin, floor) then delete;
         if _n_ < %sysevalf((&k-1)*&nsim/&nwin + 1, floor) then delete;
         Iteration + &nwin;
      run;

      proc sgplot data=save&k(firstobs=10) cycleattrs;
         series x=Iteration y=Estimate;
         series x=Iteration y=upperbound;
         yaxis label="%scan(&var, &k)";
      run;
   %end;
%mend sepPSRF;

%sepPSRF(nparm=&nparm, var=&var, nsim=&nsim);

Output 59.21.3: PSRF Plot for Each Parameter

PSRF is the square root of the ratio of the between-chain variance and the within-chain variance. A large PSRF indicates that the between-chain variance is substantially greater than the within-chain variance, so that longer simulation is needed. You want the PSRF to converge to 1 eventually, as it appears to be the case in this simulation study.