The QUANTLIFE Procedure
This example reproduces analysis done by Portnoy (2003), which demonstrates how to use quantile regression to analyze survival times. The example uses drug abuse data from Hosmer and Lemeshow (1999). The goal of this study is to compare treatment effects on reducing drug abuse.
The data set contains the following variables:
-
Time, time to return to drug use, in days -
Status, event indicator, with value 1 for return to drug use and value 0 for censored time -
Age, age at enrollment, in years -
Treatment, with value 1 for six-month treatment and value 0 for three-month treatment -
Beck, Beck Depression Inventory score at admission to the program -
IV3, indicator of recent intravenous drug use -
NDT, number of prior drug treatments -
Race, race indicator, with value 1 for white and value 0 for nonwhite -
Site, treatment sites (A and B) -
LOT, length of treatment, in days
The following statements create the data set UIS:
data uis;
input ID Age Becktota Hercoc Ivhx Ndrugtx Race Treat Site Lot Time
Censor;
Iv3 = (Ivhx = 3);
Nd1 = 1/((Ndrugtx+1)/10);
Nd2 = (1/((Ndrugtx+1)/10))*log((Ndrugtx+1)/10);
if (Treat =1 ) then Frac = Lot/180;
else Frac = Lot/90;
datalines;
1 39 9.0000 4 3 1 0 1 0 123 188 1
2 33 34.0000 4 2 8 0 1 0 25 26 1
3 33 10.0000 2 3 3 0 1 0 7 207 1
4 32 20.0000 4 3 1 0 0 0 66 144 1
... more lines ...
626 28 10.0 4 2 3 0 1 1 21 35 1
627 35 17.0 1 3 2 0 0 1 184 379 1
628 46 31.5 1 3 15 1 1 1 9 377 1
;
The following statements replicate the analysis of Portnoy (2003):
ods graphics on;
proc quantlife data=uis log seed=999 plots=(quantplot survival);
class Race Site Treat;
model Time*Censor(0)=Nd1 Nd2 Iv3 Becktota
Treat Frac Race Age|Site
/ quantile=0.05 to 0.85 by 0.05 ;
baseline out=Predsurvf;
run;
Output 80.2.1 displays the model information. Out of 628 subjects, 53 contain missing values and are not included in the analysis. The censoring rate is 20.87%.
Output 80.2.1: Model Information
| Model Information | |
|---|---|
| Data Set | WORK.UIS |
| Dependent Variable | Log(Time) |
| Censoring Variable | Censor |
| Censoring Value(s) | 0 |
| Number of Observations | 575 |
| Method | Kaplan-Meier |
| Replications | 200 |
| Seed for Random Number Generator | 999 |
| Class Level Information | ||
|---|---|---|
| Name | Levels | Values |
| Race | 2 | 0 1 |
| Site | 2 | 0 1 |
| Treat | 2 | 0 1 |
| Summary of the Number of Event and Censored Values |
|||
|---|---|---|---|
| Total | Event | Censored | Percent Censored |
| 575 | 464 | 111 | 19.30 |
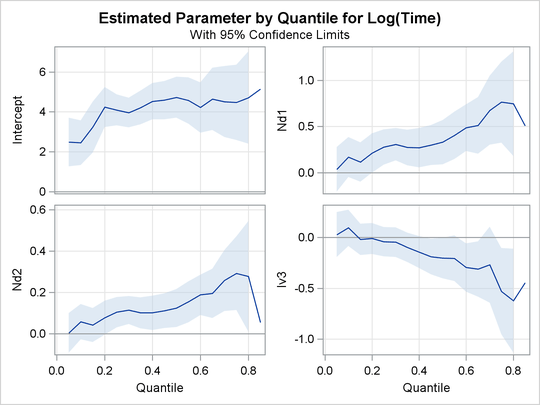
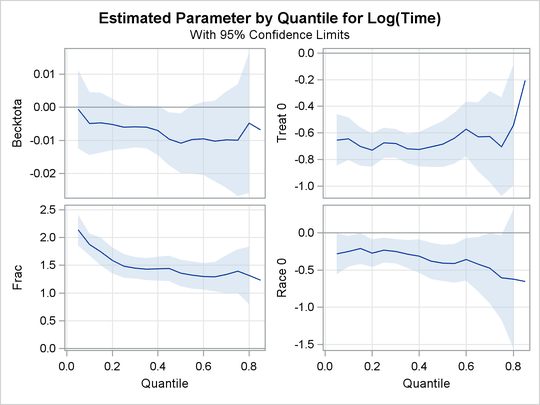
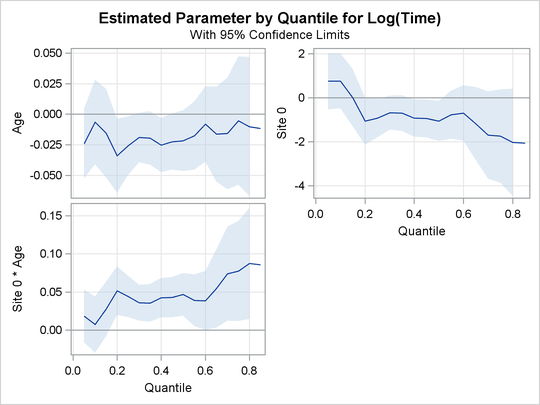
Output 80.2.2, Output 80.2.3, and Output 80.2.4 display regression quantile process plots for each covariate.
You can see the varying effects for Nd and Frac, whereas the treatment effect is fairly constant. For more information about the covariate effects that can be discovered
using quantile regression, see Portnoy (2003).
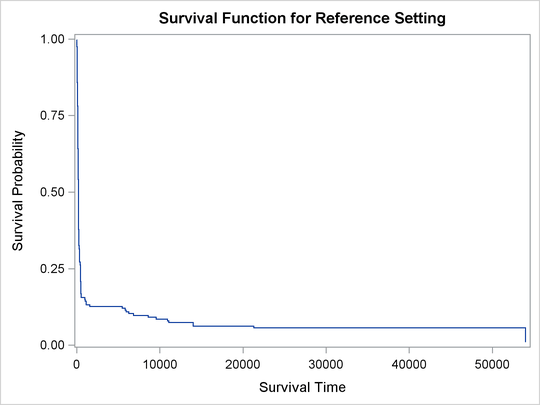
In survival analysis, a plot of the estimated survival function is often of interest. There is a one-to-one relationship between the quantile function and the survival function. When you specify the PLOTS= SURVIVAL option, the QUANTLIFE procedure estimates the survival function by fitting a quantile regression model for a grid of equally spaced quantile levels. You can specify the grid points by using the INITTAU=option and the step between adjacent grid points by using the GRIDSIZE=option. For more information, see the section Kaplan-Meier-Type Estimator for Censored Quantile Regression.
Figure 80.4 shows the estimated survival function at the reference set of covariate values that consist of reference levels for the CLASS variables and average values for the continuous variables. You can output the predicted survival function by specifying the SURVIVAL= option in the BASELINE statement.